Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 17771 by b.e.h.i.8.3.417@gmail.com last updated on 10/Jul/17

Commented by b.e.h.i.8.3.417@gmail.com last updated on 10/Jul/17

in XY^Δ Z: 1)XY=XZ 2)XS=ST=TZ=ZY find any possible angles in this triangle, by using this two conditions.

$${in}\:{X}\overset{\Delta} {{Y}Z}:\: \\ $$$$\left.\:\:\:\:\mathrm{1}\right){XY}={XZ} \\ $$$$\left.\:\:\:\:\mathrm{2}\right){XS}={ST}={TZ}={ZY}\:\: \\ $$$${find}\:{any}\:{possible}\:{angles}\:{in}\:{this}\: \\ $$$${triangle},\:{by}\:{using}\:{this}\:{two}\:{conditions}. \\ $$

Answered by mrW1 last updated on 10/Jul/17

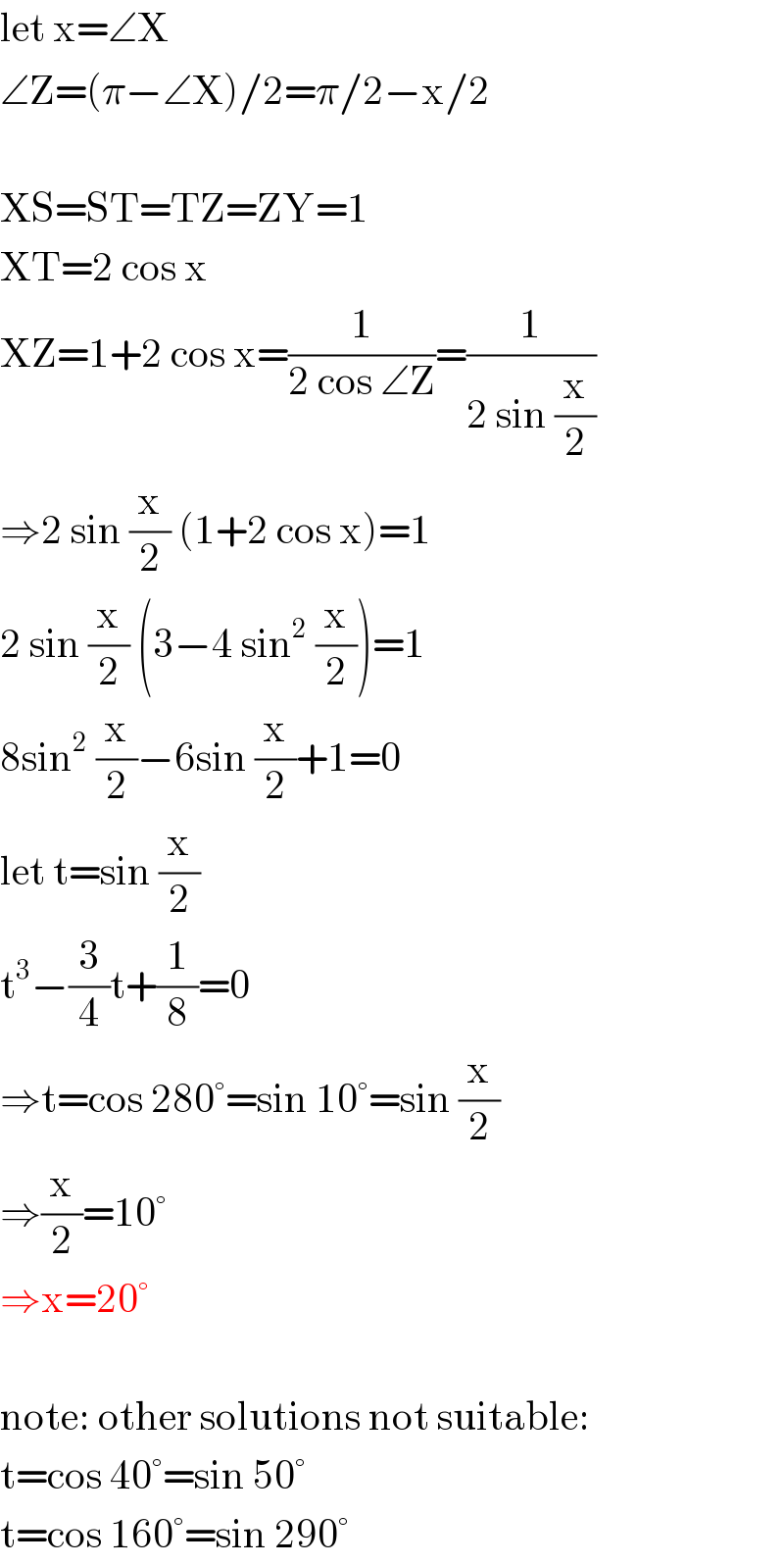
let x=∠X ∠Z=(π−∠X)/2=π/2−x/2 XS=ST=TZ=ZY=1 XT=2 cos x XZ=1+2 cos x=(1/(2 cos ∠Z))=(1/(2 sin (x/2))) ⇒2 sin (x/2) (1+2 cos x)=1 2 sin (x/2) (3−4 sin^2 (x/2))=1 8sin^2 (x/2)−6sin (x/2)+1=0 let t=sin (x/2) t^3 −(3/4)t+(1/8)=0 ⇒t=cos 280°=sin 10°=sin (x/2) ⇒(x/2)=10° ⇒x=20° note: other solutions not suitable: t=cos 40°=sin 50° t=cos 160°=sin 290°

$$\mathrm{let}\:\mathrm{x}=\angle\mathrm{X} \\ $$$$\angle\mathrm{Z}=\left(\pi−\angle\mathrm{X}\right)/\mathrm{2}=\pi/\mathrm{2}−\mathrm{x}/\mathrm{2} \\ $$$$ \\ $$$$\mathrm{XS}=\mathrm{ST}=\mathrm{TZ}=\mathrm{ZY}=\mathrm{1} \\ $$$$\mathrm{XT}=\mathrm{2}\:\mathrm{cos}\:\mathrm{x} \\ $$$$\mathrm{XZ}=\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\mathrm{x}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{cos}\:\angle\mathrm{Z}}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}\:\left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\mathrm{x}\right)=\mathrm{1} \\ $$$$\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}\:\left(\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{1} \\ $$$$\mathrm{8sin}^{\mathrm{2}} \:\frac{\mathrm{x}}{\mathrm{2}}−\mathrm{6sin}\:\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{let}\:\mathrm{t}=\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}} \\ $$$$\mathrm{t}^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{4}}\mathrm{t}+\frac{\mathrm{1}}{\mathrm{8}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{t}=\mathrm{cos}\:\mathrm{280}°=\mathrm{sin}\:\mathrm{10}°=\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{x}}{\mathrm{2}}=\mathrm{10}° \\ $$$$\Rightarrow\mathrm{x}=\mathrm{20}° \\ $$$$ \\ $$$$\mathrm{note}:\:\mathrm{other}\:\mathrm{solutions}\:\mathrm{not}\:\mathrm{suitable}: \\ $$$$\mathrm{t}=\mathrm{cos}\:\mathrm{40}°=\mathrm{sin}\:\mathrm{50}° \\ $$$$\mathrm{t}=\mathrm{cos}\:\mathrm{160}°=\mathrm{sin}\:\mathrm{290}° \\ $$

Commented by ajfour last updated on 11/Jul/17

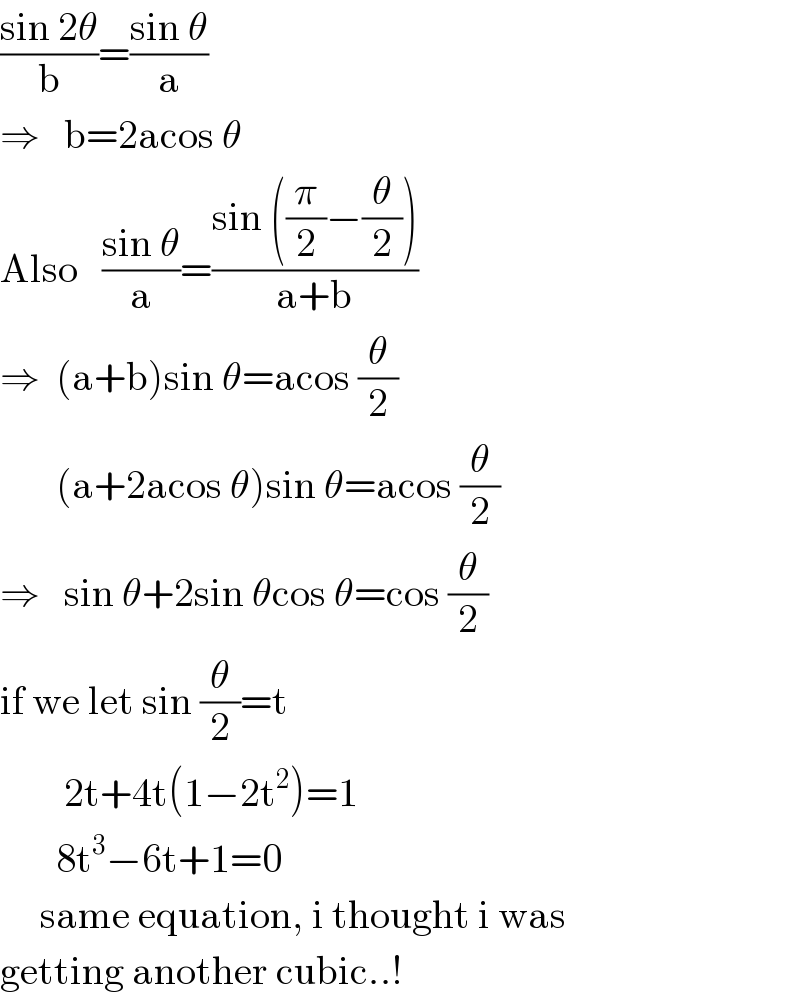
((sin 2θ)/b)=((sin θ)/a) ⇒ b=2acos θ Also ((sin θ)/a)=((sin ((π/2)−(θ/2)))/(a+b)) ⇒ (a+b)sin θ=acos (θ/2) (a+2acos θ)sin θ=acos (θ/2) ⇒ sin θ+2sin θcos θ=cos (θ/2) if we let sin (θ/2)=t 2t+4t(1−2t^2 )=1 8t^3 −6t+1=0 same equation, i thought i was getting another cubic..!

$$\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{b}}=\frac{\mathrm{sin}\:\theta}{\mathrm{a}} \\ $$$$\Rightarrow\:\:\:\mathrm{b}=\mathrm{2acos}\:\theta \\ $$$$\mathrm{Also}\:\:\:\frac{\mathrm{sin}\:\theta}{\mathrm{a}}=\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\frac{\theta}{\mathrm{2}}\right)}{\mathrm{a}+\mathrm{b}} \\ $$$$\Rightarrow\:\:\left(\mathrm{a}+\mathrm{b}\right)\mathrm{sin}\:\theta=\mathrm{acos}\:\frac{\theta}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\left(\mathrm{a}+\mathrm{2acos}\:\theta\right)\mathrm{sin}\:\theta=\mathrm{acos}\:\frac{\theta}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\mathrm{sin}\:\theta+\mathrm{2sin}\:\theta\mathrm{cos}\:\theta=\mathrm{cos}\:\frac{\theta}{\mathrm{2}} \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{let}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\mathrm{t}\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{2t}+\mathrm{4t}\left(\mathrm{1}−\mathrm{2t}^{\mathrm{2}} \right)=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\mathrm{8t}^{\mathrm{3}} −\mathrm{6t}+\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{same}\:\mathrm{equation},\:\mathrm{i}\:\mathrm{thought}\:\mathrm{i}\:\mathrm{was} \\ $$$$\mathrm{getting}\:\mathrm{another}\:\mathrm{cubic}..! \\ $$

Commented by ajfour last updated on 11/Jul/17

Commented by b.e.h.i.8.3.417@gmail.com last updated on 11/Jul/17

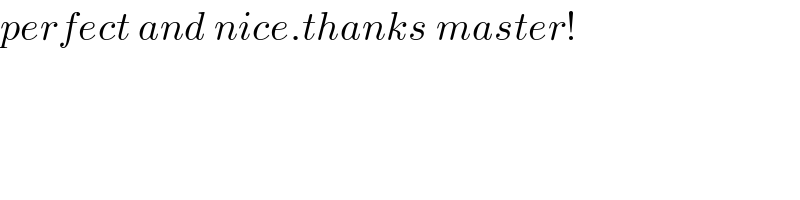
perfect and nice.thanks master!

$${perfect}\:{and}\:{nice}.{thanks}\:{master}! \\ $$

Commented by mrW1 last updated on 11/Jul/17

thank you for trying from an other aspect. the solution of the cubic eqn. is in this case simple, they are cos 40°, cos 160° and cos 280°. but we can use a trick to make it easier. let α=(θ/2) we have got 8 sin^3 α −6 sin α +1=0 ⇒1−2(3 sin α−4 sin^3 α)=0 on the other side we know sin 3α=3 sin α−4 sin^3 α ⇒1−2 sin 3α=0 ⇒sin 3α=(1/2) ⇒3α=30° ⇒α=10°=(θ/2) ⇒θ=20°

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{trying}\:\mathrm{from}\:\mathrm{an}\:\mathrm{other} \\ $$$$\mathrm{aspect}.\: \\ $$$$\mathrm{the}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{the}\:\mathrm{cubic}\:\mathrm{eqn}.\:\mathrm{is}\:\mathrm{in}\:\mathrm{this} \\ $$$$\mathrm{case}\:\mathrm{simple},\:\mathrm{they}\:\mathrm{are}\:\mathrm{cos}\:\mathrm{40}°,\:\mathrm{cos}\:\mathrm{160}° \\ $$$$\mathrm{and}\:\mathrm{cos}\:\mathrm{280}°. \\ $$$$ \\ $$$$\mathrm{but}\:\mathrm{we}\:\mathrm{can}\:\mathrm{use}\:\mathrm{a}\:\mathrm{trick}\:\mathrm{to}\:\mathrm{make}\:\mathrm{it}\:\mathrm{easier}. \\ $$$$\mathrm{let}\:\alpha=\frac{\theta}{\mathrm{2}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{got}\: \\ $$$$\mathrm{8}\:\mathrm{sin}^{\mathrm{3}} \:\alpha\:−\mathrm{6}\:\mathrm{sin}\:\alpha\:+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}−\mathrm{2}\left(\mathrm{3}\:\mathrm{sin}\:\alpha−\mathrm{4}\:\mathrm{sin}^{\mathrm{3}} \:\alpha\right)=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{on}\:\mathrm{the}\:\mathrm{other}\:\mathrm{side}\:\mathrm{we}\:\mathrm{know} \\ $$$$\mathrm{sin}\:\mathrm{3}\alpha=\mathrm{3}\:\mathrm{sin}\:\alpha−\mathrm{4}\:\mathrm{sin}^{\mathrm{3}} \:\alpha \\ $$$$ \\ $$$$\Rightarrow\mathrm{1}−\mathrm{2}\:\mathrm{sin}\:\mathrm{3}\alpha=\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{3}\alpha=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{3}\alpha=\mathrm{30}° \\ $$$$\Rightarrow\alpha=\mathrm{10}°=\frac{\theta}{\mathrm{2}} \\ $$$$\Rightarrow\theta=\mathrm{20}° \\ $$

Commented by b.e.h.i.8.3.417@gmail.com last updated on 11/Jul/17

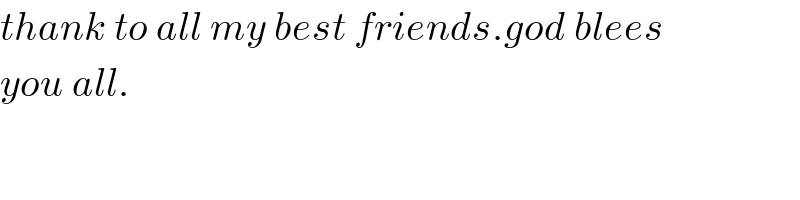
thank to all my best friends.god blees you all.

$${thank}\:{to}\:{all}\:{my}\:{best}\:{friends}.{god}\:{blees} \\ $$$${you}\:{all}. \\ $$

Commented by ajfour last updated on 11/Jul/17

thanks for enlightening further sir. i was wondering how the cubic yielded θ=20°.

$$\mathrm{thanks}\:\mathrm{for}\:\mathrm{enlightening}\:\mathrm{further}\:\mathrm{sir}. \\ $$$$\mathrm{i}\:\mathrm{was}\:\mathrm{wondering}\:\mathrm{how}\:\mathrm{the}\:\mathrm{cubic} \\ $$$$\mathrm{yielded}\:\theta=\mathrm{20}°. \\ $$

Commented by mrW1 last updated on 11/Jul/17

I solved the cubic eqn. directly without using the trick above. t^3 −(3/4)t+(1/8)=0 ⇒t^3 +3pt+q=0 ...(i) with p=−(1/4) and q=(1/8) the solution of (i) is following: D=q^2 +4p^3 =(1/8^2 )−(4/4^3 )=−(3/(64))<0 ⇒there are 3 real roots: t_1 =2 (√(−p)) cos ((ϕ/3)) t_2 =2 (√(−p)) cos ((ϕ/3)+120°) t_3 =2 (√(−p)) cos ((ϕ/3)+240°) with cos ϕ=((−q)/(2 (√(−p^3 ))))=((−1/8)/(2×1/8))=−(1/2) ⇒ϕ=120° ⇒ϕ/3=40° ⇒t_1 =2 (√(−p)) cos ((ϕ/3))=2×(1/2)×cos 40°=cos 40° ⇒t_2 =2 (√(−p)) cos ((ϕ/3)+120°)=cos 160° ⇒t_3 =2 (√(−p)) cos ((ϕ/3)+240°)=cos 280° but only t_3 =cos 280° is suitable, since cos 280°=sin 10° ⇒t=sin (x/2)=sin 10° ⇒x=20°

$$\mathrm{I}\:\mathrm{solved}\:\mathrm{the}\:\mathrm{cubic}\:\mathrm{eqn}.\:\mathrm{directly}\:\mathrm{without} \\ $$$$\mathrm{using}\:\mathrm{the}\:\mathrm{trick}\:\mathrm{above}. \\ $$$$\mathrm{t}^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{4}}\mathrm{t}+\frac{\mathrm{1}}{\mathrm{8}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{t}^{\mathrm{3}} +\mathrm{3pt}+\mathrm{q}=\mathrm{0}\:\:...\left(\mathrm{i}\right) \\ $$$$\mathrm{with}\:\mathrm{p}=−\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{and}\:\mathrm{q}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\mathrm{the}\:\mathrm{solution}\:\mathrm{of}\:\left(\mathrm{i}\right)\:\mathrm{is}\:\mathrm{following}: \\ $$$$\mathrm{D}=\mathrm{q}^{\mathrm{2}} +\mathrm{4p}^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{8}^{\mathrm{2}} }−\frac{\mathrm{4}}{\mathrm{4}^{\mathrm{3}} }=−\frac{\mathrm{3}}{\mathrm{64}}<\mathrm{0} \\ $$$$\Rightarrow\mathrm{there}\:\mathrm{are}\:\mathrm{3}\:\mathrm{real}\:\mathrm{roots}: \\ $$$$\mathrm{t}_{\mathrm{1}} =\mathrm{2}\:\sqrt{−\mathrm{p}}\:\mathrm{cos}\:\left(\frac{\varphi}{\mathrm{3}}\right) \\ $$$$\mathrm{t}_{\mathrm{2}} =\mathrm{2}\:\sqrt{−\mathrm{p}}\:\mathrm{cos}\:\left(\frac{\varphi}{\mathrm{3}}+\mathrm{120}°\right) \\ $$$$\mathrm{t}_{\mathrm{3}} =\mathrm{2}\:\sqrt{−\mathrm{p}}\:\mathrm{cos}\:\left(\frac{\varphi}{\mathrm{3}}+\mathrm{240}°\right) \\ $$$$\mathrm{with}\:\mathrm{cos}\:\varphi=\frac{−\mathrm{q}}{\mathrm{2}\:\sqrt{−\mathrm{p}^{\mathrm{3}} }}=\frac{−\mathrm{1}/\mathrm{8}}{\mathrm{2}×\mathrm{1}/\mathrm{8}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\varphi=\mathrm{120}° \\ $$$$\Rightarrow\varphi/\mathrm{3}=\mathrm{40}° \\ $$$$\Rightarrow\mathrm{t}_{\mathrm{1}} =\mathrm{2}\:\sqrt{−\mathrm{p}}\:\mathrm{cos}\:\left(\frac{\varphi}{\mathrm{3}}\right)=\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{cos}\:\mathrm{40}°=\mathrm{cos}\:\mathrm{40}° \\ $$$$\Rightarrow\mathrm{t}_{\mathrm{2}} =\mathrm{2}\:\sqrt{−\mathrm{p}}\:\mathrm{cos}\:\left(\frac{\varphi}{\mathrm{3}}+\mathrm{120}°\right)=\mathrm{cos}\:\mathrm{160}° \\ $$$$\Rightarrow\mathrm{t}_{\mathrm{3}} =\mathrm{2}\:\sqrt{−\mathrm{p}}\:\mathrm{cos}\:\left(\frac{\varphi}{\mathrm{3}}+\mathrm{240}°\right)=\mathrm{cos}\:\mathrm{280}° \\ $$$$ \\ $$$$\mathrm{but}\:\mathrm{only}\:\mathrm{t}_{\mathrm{3}} =\mathrm{cos}\:\mathrm{280}°\:\mathrm{is}\:\mathrm{suitable},\:\mathrm{since} \\ $$$$\mathrm{cos}\:\mathrm{280}°=\mathrm{sin}\:\mathrm{10}° \\ $$$$\Rightarrow\mathrm{t}=\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}=\mathrm{sin}\:\mathrm{10}° \\ $$$$\Rightarrow\mathrm{x}=\mathrm{20}° \\ $$

Commented by ajfour last updated on 11/Jul/17

thanks Sir, let me consult some more literature on solution of cubic equations.

$$\mathrm{thanks}\:\mathrm{Sir},\:\mathrm{let}\:\mathrm{me}\:\mathrm{consult}\:\mathrm{some} \\ $$$$\mathrm{more}\:\mathrm{literature}\:\mathrm{on}\:\mathrm{solution}\:\mathrm{of} \\ $$$$\mathrm{cubic}\:\mathrm{equations}.\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com