Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 177815 by infinityaction last updated on 09/Oct/22

Answered by mahdipoor last updated on 09/Oct/22

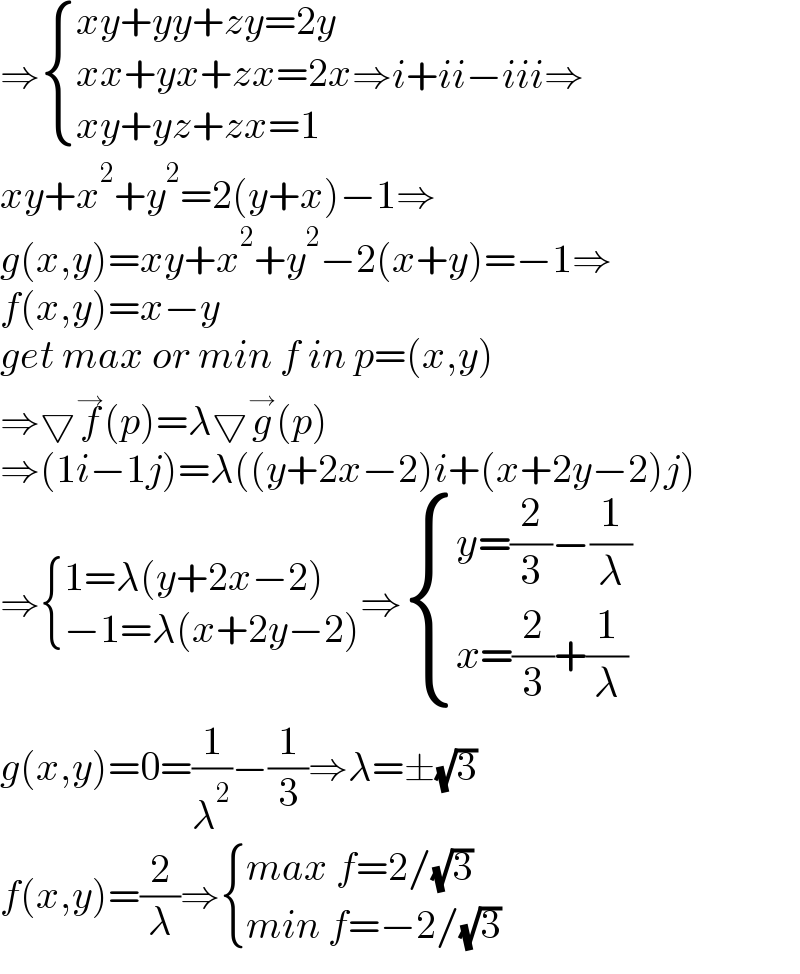
⇒ { ((xy+yy+zy=2y)),((xx+yx+zx=2x)),((xy+yz+zx=1)) :}⇒i+ii−iii⇒ xy+x^2 +y^2 =2(y+x)−1⇒ g(x,y)=xy+x^2 +y^2 −2(x+y)=−1⇒ f(x,y)=x−y get max or min f in p=(x,y) ⇒▽f^→ (p)=λ▽g^→ (p) ⇒(1i−1j)=λ((y+2x−2)i+(x+2y−2)j) ⇒ { ((1=λ(y+2x−2))),((−1=λ(x+2y−2))) :}⇒ { ((y=(2/3)−(1/λ))),((x=(2/3)+(1/λ))) :} g(x,y)=0=(1/λ^2 )−(1/3)⇒λ=±(√3) f(x,y)=(2/λ)⇒ { ((max f=2/(√3))),((min f=−2/(√3))) :}

$$\Rightarrow\begin{cases}{{xy}+{yy}+{zy}=\mathrm{2}{y}}\\{{xx}+{yx}+{zx}=\mathrm{2}{x}}\\{{xy}+{yz}+{zx}=\mathrm{1}}\end{cases}\Rightarrow{i}+{ii}−{iii}\Rightarrow \\ $$$${xy}+{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{2}\left({y}+{x}\right)−\mathrm{1}\Rightarrow \\ $$$${g}\left({x},{y}\right)={xy}+{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}\left({x}+{y}\right)=−\mathrm{1}\Rightarrow \\ $$$${f}\left({x},{y}\right)={x}−{y} \\ $$$${get}\:{max}\:{or}\:{min}\:{f}\:{in}\:{p}=\left({x},{y}\right) \\ $$$$\Rightarrow\bigtriangledown\overset{\rightarrow} {{f}}\left({p}\right)=\lambda\bigtriangledown\overset{\rightarrow} {{g}}\left({p}\right) \\ $$$$\Rightarrow\left(\mathrm{1}{i}−\mathrm{1}{j}\right)=\lambda\left(\left({y}+\mathrm{2}{x}−\mathrm{2}\right){i}+\left({x}+\mathrm{2}{y}−\mathrm{2}\right){j}\right) \\ $$$$\Rightarrow\begin{cases}{\mathrm{1}=\lambda\left({y}+\mathrm{2}{x}−\mathrm{2}\right)}\\{−\mathrm{1}=\lambda\left({x}+\mathrm{2}{y}−\mathrm{2}\right)}\end{cases}\Rightarrow\begin{cases}{{y}=\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{1}}{\lambda}}\\{{x}=\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{1}}{\lambda}}\end{cases} \\ $$$${g}\left({x},{y}\right)=\mathrm{0}=\frac{\mathrm{1}}{\lambda^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow\lambda=\pm\sqrt{\mathrm{3}} \\ $$$${f}\left({x},{y}\right)=\frac{\mathrm{2}}{\lambda}\Rightarrow\begin{cases}{{max}\:{f}=\mathrm{2}/\sqrt{\mathrm{3}}}\\{{min}\:{f}=−\mathrm{2}/\sqrt{\mathrm{3}}}\end{cases} \\ $$

Commented by infinityaction last updated on 09/Oct/22

thanks sir

$${thanks}\:{sir} \\ $$

Commented by Tawa11 last updated on 10/Oct/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Answered by mr W last updated on 09/Oct/22

x+y=2−z xy+(x+y)z=1 xy=1−z(2−z) (x−y)^2 =(x+y)^2 −4xy =(2−z)^2 −4[1−z(2−z)] =4z−3z^2 =−3(z−(2/3))^2 +(4/3)≤(4/3) ⇒∣x−y∣≤(2/( (√3))) ⇒−(2/( (√3)))≤x−y≤(2/( (√3))) ⇒(x−y)_(max) =(2/( (√3))) at z=(2/3) ⇒(x−y)_(min) =−(2/( (√3))) at z=(2/3)

$${x}+{y}=\mathrm{2}−{z} \\ $$$${xy}+\left({x}+{y}\right){z}=\mathrm{1} \\ $$$${xy}=\mathrm{1}−{z}\left(\mathrm{2}−{z}\right) \\ $$$$\left({x}−{y}\right)^{\mathrm{2}} =\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{4}{xy} \\ $$$$\:\:=\left(\mathrm{2}−{z}\right)^{\mathrm{2}} −\mathrm{4}\left[\mathrm{1}−{z}\left(\mathrm{2}−{z}\right)\right] \\ $$$$\:\:=\mathrm{4}{z}−\mathrm{3}{z}^{\mathrm{2}} \\ $$$$\:\:=−\mathrm{3}\left({z}−\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{4}}{\mathrm{3}}\leqslant\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\Rightarrow\mid{x}−{y}\mid\leqslant\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\leqslant{x}−{y}\leqslant\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\left({x}−{y}\right)_{{max}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:{at}\:{z}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow\left({x}−{y}\right)_{{min}} =−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:{at}\:{z}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$

Commented by infinityaction last updated on 09/Oct/22

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Commented by Tawa11 last updated on 10/Oct/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com