
Question and Answers Forum
Question Number 177900 by yaslm last updated on 10/Oct/22
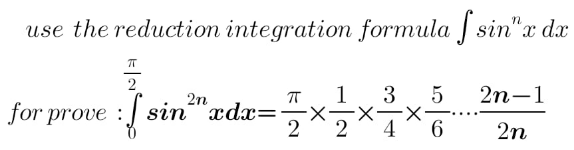
Answered by Ar Brandon last updated on 11/Oct/22
![I_n =∫_0 ^(π/2) sin^n xdx I_(n+2) =∫_0 ^(π/2) sin^(n+2) xdx =∫_0 ^(π/2) sin^n xsin^2 xdx=∫_0 ^(π/2) sin^n x(1−cos^2 x)dx =∫_0 ^(π/2) sin^n xdx−∫_0 ^(π/2) sin^n xcos^2 xdx =I_n −∫_0 ^(π/2) (sin^n xcosx)cosxdx =I_n −[((sin^(n+1) x)/(n+1))cosx]_0 ^(π/2) −(1/(n+1))∫_0 ^(π/2) (sin^(n+1) x)sinxdx =I_n −(1/(n+1))∫_0 ^(π/2) sin^(n+2) xdx=I_n −(1/(n+1))I_(n+2) ⇒(1+(1/(n+1)))I_(n+2) =I_n ⇒(((n+2)/(n+1)))I_(n+2) =I_n ⇒I_(n+2) =((n+1)/(n+2))I_n ⇒I_(2n) =((2n−1)/(2n))I_(2n−2) =((2n−1)/(2n))∙((2n−3)/(2n−2))∙((2n−5)/(2n−4))∙∙∙(3/4)∙(1/2)I_0 I_0 =∫_0 ^(π/2) (sinx)^0 dx=∫_0 ^(π/2) dx=(π/2) ⇒I_(2n) =((2n−1)/(2n))∙((2n−3)/(2n−2))∙((2n−5)/(2n−4))∙∙∙(3/4)∙(1/2)∙(π/2)](Q177903.png)
Commented by yaslm last updated on 11/Oct/22
thank you so much
| ||
Question and Answers Forum | ||
Question Number 177900 by yaslm last updated on 10/Oct/22 | ||
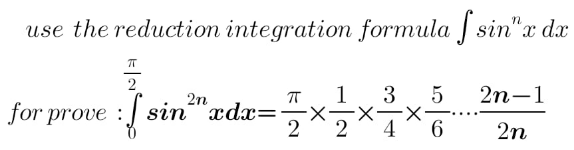 | ||
Answered by Ar Brandon last updated on 11/Oct/22 | ||
![I_n =∫_0 ^(π/2) sin^n xdx I_(n+2) =∫_0 ^(π/2) sin^(n+2) xdx =∫_0 ^(π/2) sin^n xsin^2 xdx=∫_0 ^(π/2) sin^n x(1−cos^2 x)dx =∫_0 ^(π/2) sin^n xdx−∫_0 ^(π/2) sin^n xcos^2 xdx =I_n −∫_0 ^(π/2) (sin^n xcosx)cosxdx =I_n −[((sin^(n+1) x)/(n+1))cosx]_0 ^(π/2) −(1/(n+1))∫_0 ^(π/2) (sin^(n+1) x)sinxdx =I_n −(1/(n+1))∫_0 ^(π/2) sin^(n+2) xdx=I_n −(1/(n+1))I_(n+2) ⇒(1+(1/(n+1)))I_(n+2) =I_n ⇒(((n+2)/(n+1)))I_(n+2) =I_n ⇒I_(n+2) =((n+1)/(n+2))I_n ⇒I_(2n) =((2n−1)/(2n))I_(2n−2) =((2n−1)/(2n))∙((2n−3)/(2n−2))∙((2n−5)/(2n−4))∙∙∙(3/4)∙(1/2)I_0 I_0 =∫_0 ^(π/2) (sinx)^0 dx=∫_0 ^(π/2) dx=(π/2) ⇒I_(2n) =((2n−1)/(2n))∙((2n−3)/(2n−2))∙((2n−5)/(2n−4))∙∙∙(3/4)∙(1/2)∙(π/2)](Q177903.png) | ||
| ||
Commented by yaslm last updated on 11/Oct/22 | ||
thank you so much | ||