
Question Number 177957 by infinityaction last updated on 11/Oct/22
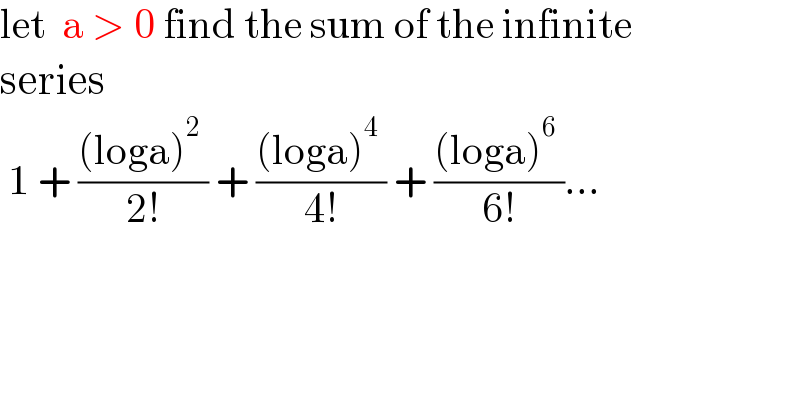
$$\mathrm{let}\:\:\mathrm{a}\:>\:\mathrm{0}\:\mathrm{find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{infinite}\: \\ $$ $$\mathrm{series} \\ $$ $$\:\mathrm{1}\:+\:\frac{\left(\mathrm{loga}\right)^{\mathrm{2}} \:}{\mathrm{2}!}\:+\:\frac{\left(\mathrm{loga}\right)^{\mathrm{4}} \:}{\mathrm{4}!}\:+\:\frac{\left(\mathrm{loga}\right)^{\mathrm{6}} \:}{\mathrm{6}!}... \\ $$
Answered by mr W last updated on 11/Oct/22
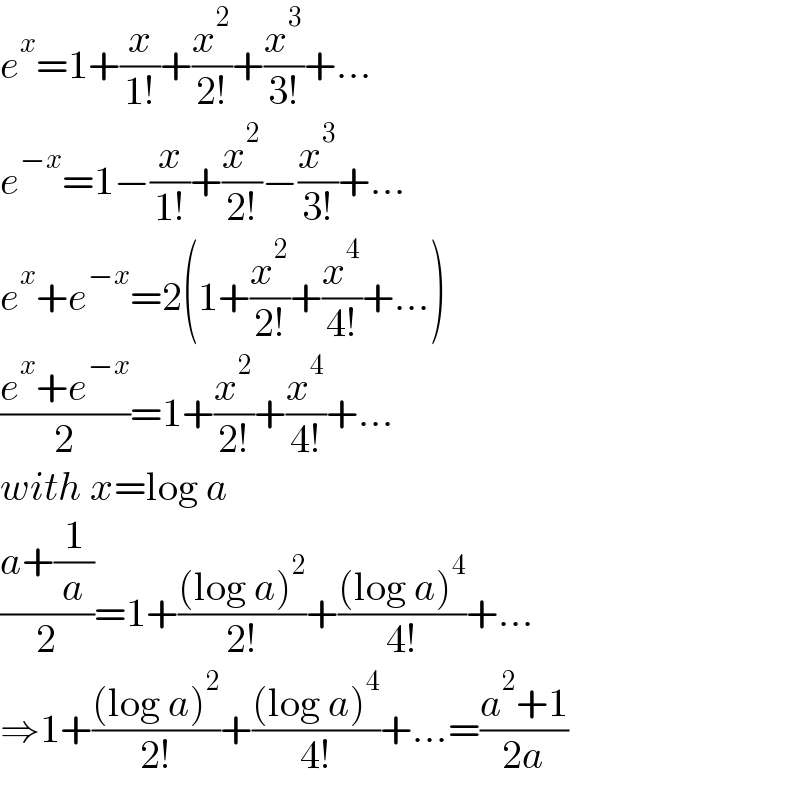
$${e}^{{x}} =\mathrm{1}+\frac{{x}}{\mathrm{1}!}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+... \\ $$ $${e}^{−{x}} =\mathrm{1}−\frac{{x}}{\mathrm{1}!}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+... \\ $$ $${e}^{{x}} +{e}^{−{x}} =\mathrm{2}\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}+...\right) \\ $$ $$\frac{{e}^{{x}} +{e}^{−{x}} }{\mathrm{2}}=\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}+... \\ $$ $${with}\:{x}=\mathrm{log}\:{a} \\ $$ $$\frac{{a}+\frac{\mathrm{1}}{{a}}}{\mathrm{2}}=\mathrm{1}+\frac{\left(\mathrm{log}\:{a}\right)^{\mathrm{2}} }{\mathrm{2}!}+\frac{\left(\mathrm{log}\:{a}\right)^{\mathrm{4}} }{\mathrm{4}!}+... \\ $$ $$\Rightarrow\mathrm{1}+\frac{\left(\mathrm{log}\:{a}\right)^{\mathrm{2}} }{\mathrm{2}!}+\frac{\left(\mathrm{log}\:{a}\right)^{\mathrm{4}} }{\mathrm{4}!}+...=\frac{{a}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{a}} \\ $$
Commented byinfinityaction last updated on 11/Oct/22

$${thank}\:{you}\:{sir} \\ $$
Commented byTawa11 last updated on 11/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by Ar Brandon last updated on 11/Oct/22
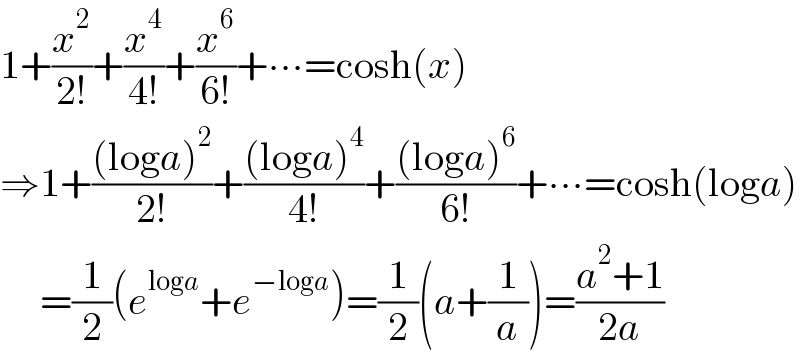
$$\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}+\frac{{x}^{\mathrm{6}} }{\mathrm{6}!}+\centerdot\centerdot\centerdot=\mathrm{cosh}\left({x}\right) \\ $$ $$\Rightarrow\mathrm{1}+\frac{\left(\mathrm{log}{a}\right)^{\mathrm{2}} }{\mathrm{2}!}+\frac{\left(\mathrm{log}{a}\right)^{\mathrm{4}} }{\mathrm{4}!}+\frac{\left(\mathrm{log}{a}\right)^{\mathrm{6}} }{\mathrm{6}!}+\centerdot\centerdot\centerdot=\mathrm{cosh}\left(\mathrm{log}{a}\right) \\ $$ $$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left({e}^{\mathrm{log}{a}} +{e}^{−\mathrm{log}{a}} \right)=\frac{\mathrm{1}}{\mathrm{2}}\left({a}+\frac{\mathrm{1}}{{a}}\right)=\frac{{a}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{a}} \\ $$
Commented byTawa11 last updated on 11/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
