
Question and Answers Forum
Question Number 178246 by mnjuly1970 last updated on 14/Oct/22
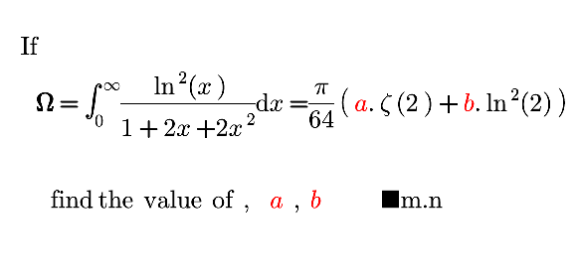
Answered by CElcedricjunior last updated on 14/Oct/22
![𝛀=∫_0 ^∞ ((ln^2 (x))/(1+2x+2x^2 ))dx=(𝛑/(64))(a𝛇(2)+bln^2 (2)) 𝛀=∫_0 ^∞ ((ln^2 (x))/(1+2x+2x^2 ))=∫_0 ^∞ ((ln^2 (x))/(2[(x+(1/2))^2 +(1/4)]))dx 𝛀=2∫_0 ^∞ ((ln^2 (x))/((2x+1)^2 +1))dx posons 2x+1=tana=>x=(1/2)(tana−1) =>dx=(1/2)(1+tan^2 a)da qd: { ((x−>0)),((x−>∞)) :}=> { ((a−>(𝛑/4))),((a−>(𝛑/2))) :} =>𝛀=2∫_(π/4) ^(π/2) ln^2 ((1/2)(tana−1))dx =>𝛀=2∫_(𝛑/4) ^(𝛑/2) ln^2 ((1/2))da+2∫_(π/4) ^(π/2) ln^2 (tana−1)da =>𝛀=(𝛑/2)ln^2 (2)+2∫_(𝛑/4) ^(𝛑/2) ln^2 (tana−1)da on a I=2∫_(𝛑/4) ^(𝛑/2) ln^2 (tana−1)da posons tana=x=>da=(dx/(1+x^2 )) =>I=2∫_1 ^∞ ((ln^2 (x−1))/(1+x^2 ))dx=2∫_1 ^∞ (1/(1+x^2 )).𝛇(2)dx I=2𝛇(2)∫_1 ^∞ (dx/(1+x^2 ))=2𝛇(2)[a]_(𝛑/4) ^(𝛑/2) I=((𝛑𝛇(2))/2) =>𝛀=(𝛑/2)(𝛇(2)+ln^2 (2)) =>𝛀=(𝛑/(64))(32ln^2 (2)+32𝛇(2)) ...............le celebre cedric junior.........](Q178285.png)
Commented by mnjuly1970 last updated on 14/Oct/22

Commented by Tawa11 last updated on 14/Oct/22

| ||
Question and Answers Forum | ||
Question Number 178246 by mnjuly1970 last updated on 14/Oct/22 | ||
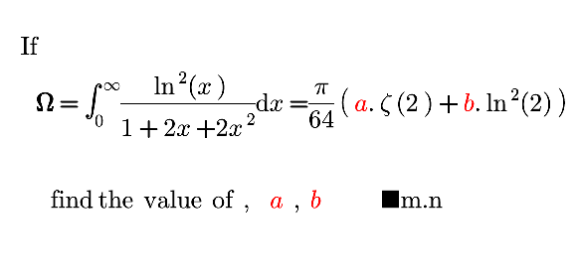 | ||
Answered by CElcedricjunior last updated on 14/Oct/22 | ||
![𝛀=∫_0 ^∞ ((ln^2 (x))/(1+2x+2x^2 ))dx=(𝛑/(64))(a𝛇(2)+bln^2 (2)) 𝛀=∫_0 ^∞ ((ln^2 (x))/(1+2x+2x^2 ))=∫_0 ^∞ ((ln^2 (x))/(2[(x+(1/2))^2 +(1/4)]))dx 𝛀=2∫_0 ^∞ ((ln^2 (x))/((2x+1)^2 +1))dx posons 2x+1=tana=>x=(1/2)(tana−1) =>dx=(1/2)(1+tan^2 a)da qd: { ((x−>0)),((x−>∞)) :}=> { ((a−>(𝛑/4))),((a−>(𝛑/2))) :} =>𝛀=2∫_(π/4) ^(π/2) ln^2 ((1/2)(tana−1))dx =>𝛀=2∫_(𝛑/4) ^(𝛑/2) ln^2 ((1/2))da+2∫_(π/4) ^(π/2) ln^2 (tana−1)da =>𝛀=(𝛑/2)ln^2 (2)+2∫_(𝛑/4) ^(𝛑/2) ln^2 (tana−1)da on a I=2∫_(𝛑/4) ^(𝛑/2) ln^2 (tana−1)da posons tana=x=>da=(dx/(1+x^2 )) =>I=2∫_1 ^∞ ((ln^2 (x−1))/(1+x^2 ))dx=2∫_1 ^∞ (1/(1+x^2 )).𝛇(2)dx I=2𝛇(2)∫_1 ^∞ (dx/(1+x^2 ))=2𝛇(2)[a]_(𝛑/4) ^(𝛑/2) I=((𝛑𝛇(2))/2) =>𝛀=(𝛑/2)(𝛇(2)+ln^2 (2)) =>𝛀=(𝛑/(64))(32ln^2 (2)+32𝛇(2)) ...............le celebre cedric junior.........](Q178285.png) | ||
| ||
Commented by mnjuly1970 last updated on 14/Oct/22 | ||
 | ||
Commented by Tawa11 last updated on 14/Oct/22 | ||
 | ||