
Question Number 178338 by Acem last updated on 15/Oct/22

$${Let}\:{S}=\:\left\{\mathrm{1},\:\mathrm{2},\:...,\:\mathrm{9},\:\mathrm{0}\right\}\:\boldsymbol{{A}}:\:{How}\:{many}\:{multiples} \\ $$$$\:{of}\:{eight}\:{of}\:{four}\:{digits}\:{can}\:{be}\:{formed}\:{from}\:{S} \\ $$$$\:\boldsymbol{{B}}:\:{The}\:{same}\:{question}\:{for}\:{different}\:{digits} \\ $$
Commented by Acem last updated on 17/Oct/22
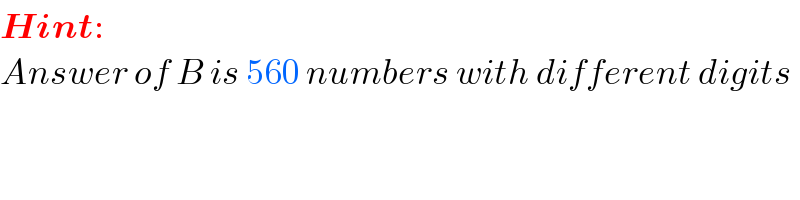
$$\boldsymbol{{Hint}}: \\ $$$${Answer}\:{of}\:{B}\:{is}\:\mathrm{560}\:{numbers}\:{with}\:{different}\:{digits} \\ $$
Answered by mr W last updated on 16/Oct/22
![[A] ⌊((9999)/8)⌋−⌊((999)/8)⌋=1249−124=1125 solution for A is simple. we just need to count the number of terms of an A.P.: 1000, 1008, 1016, ....,9992 that′s ((9992−1000)/8)+1=1125 numbers.](Q178365.png)
$$\left[\boldsymbol{{A}}\right] \\ $$$$\lfloor\frac{\mathrm{9999}}{\mathrm{8}}\rfloor−\lfloor\frac{\mathrm{999}}{\mathrm{8}}\rfloor=\mathrm{1249}−\mathrm{124}=\mathrm{1125} \\ $$$$ \\ $$$${solution}\:{for}\:{A}\:{is}\:{simple}.\:{we}\:{just}\:{need} \\ $$$${to}\:{count}\:{the}\:{number}\:{of}\:{terms}\:{of}\:{an} \\ $$$${A}.{P}.: \\ $$$$\mathrm{1000},\:\mathrm{1008},\:\mathrm{1016},\:....,\mathrm{9992} \\ $$$${that}'{s}\:\frac{\mathrm{9992}−\mathrm{1000}}{\mathrm{8}}+\mathrm{1}=\mathrm{1125}\:{numbers}. \\ $$
Commented by mr W last updated on 16/Oct/22
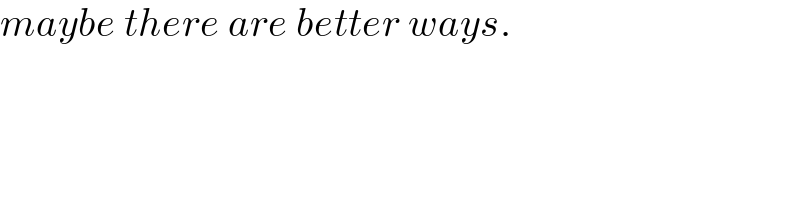
$${maybe}\:{there}\:{are}\:{better}\:{ways}. \\ $$
Commented by mr W last updated on 16/Oct/22
![[B] say such a number is ABCD with A≠B≠C≠D, A≠0 determinant (((CD=),(08),(16),(24),(32),(40),(48),(56),(64),(72),(80),(96)),(B_n ,3,(3/1),(2/1),(3/1),3,(2/1),4,(2/1),(3/1),3,(3/1)),(A_n ,7,(6/7),(6/7),(6/7),7,(6/7),(6/7),(6/7),(6/7),7,(6/7)),(,(21),(25),(19),(25),(21),(19),(25),(19),(25),(21),(25))) 21×3+25×5+19×3=245 determinant (((CD=),(04),(12),(20),(28),(36),(52),(60),(68),(76),(84),(92)),(B_n ,5,4,5,5,4,4,5,5,4,5,4),(A_n ,7,6,7,6,6,6,7,6,6,6,6),(,(35),(24),(35),(30),(24),(24),(35),(30),(24),(30),(24))) 35×3+24×5+30×3=315 ⇒totally 245+315=560 numbers with different digits ================ explanation of the table say the number is ABCD. when CD=08, B can be 2, 4, 6, i.e. 3 possibilities (B_n =3). for each B=2, A can be 1,3,4,5,6,7,9, i.e. 7 possibilities (A_n =7). ⇒3×7=21 numbers.](Q178368.png)
$$\left[\boldsymbol{{B}}\right] \\ $$$${say}\:{such}\:{a}\:{number}\:{is}\:{ABCD}\:{with} \\ $$$${A}\neq{B}\neq{C}\neq{D},\:{A}\neq\mathrm{0} \\ $$$$\begin{array}{|c|c|c|c|}{{CD}=}&\hline{\mathrm{08}}&\hline{\mathrm{16}}&\hline{\mathrm{24}}&\hline{\mathrm{32}}&\hline{\mathrm{40}}&\hline{\mathrm{48}}&\hline{\mathrm{56}}&\hline{\mathrm{64}}&\hline{\mathrm{72}}&\hline{\mathrm{80}}&\hline{\mathrm{96}}\\{{B}_{{n}} }&\hline{\mathrm{3}}&\hline{\mathrm{3}/\mathrm{1}}&\hline{\mathrm{2}/\mathrm{1}}&\hline{\mathrm{3}/\mathrm{1}}&\hline{\mathrm{3}}&\hline{\mathrm{2}/\mathrm{1}}&\hline{\mathrm{4}}&\hline{\mathrm{2}/\mathrm{1}}&\hline{\mathrm{3}/\mathrm{1}}&\hline{\mathrm{3}}&\hline{\mathrm{3}/\mathrm{1}}\\{{A}_{{n}} }&\hline{\mathrm{7}}&\hline{\mathrm{6}/\mathrm{7}}&\hline{\mathrm{6}/\mathrm{7}}&\hline{\mathrm{6}/\mathrm{7}}&\hline{\mathrm{7}}&\hline{\mathrm{6}/\mathrm{7}}&\hline{\mathrm{6}/\mathrm{7}}&\hline{\mathrm{6}/\mathrm{7}}&\hline{\mathrm{6}/\mathrm{7}}&\hline{\mathrm{7}}&\hline{\mathrm{6}/\mathrm{7}}\\{}&\hline{\mathrm{21}}&\hline{\mathrm{25}}&\hline{\mathrm{19}}&\hline{\mathrm{25}}&\hline{\mathrm{21}}&\hline{\mathrm{19}}&\hline{\mathrm{25}}&\hline{\mathrm{19}}&\hline{\mathrm{25}}&\hline{\mathrm{21}}&\hline{\mathrm{25}}\\\hline\end{array} \\ $$$$\mathrm{21}×\mathrm{3}+\mathrm{25}×\mathrm{5}+\mathrm{19}×\mathrm{3}=\mathrm{245} \\ $$$$\begin{array}{|c|c|c|c|}{{CD}=}&\hline{\mathrm{04}}&\hline{\mathrm{12}}&\hline{\mathrm{20}}&\hline{\mathrm{28}}&\hline{\mathrm{36}}&\hline{\mathrm{52}}&\hline{\mathrm{60}}&\hline{\mathrm{68}}&\hline{\mathrm{76}}&\hline{\mathrm{84}}&\hline{\mathrm{92}}\\{{B}_{{n}} }&\hline{\mathrm{5}}&\hline{\mathrm{4}}&\hline{\mathrm{5}}&\hline{\mathrm{5}}&\hline{\mathrm{4}}&\hline{\mathrm{4}}&\hline{\mathrm{5}}&\hline{\mathrm{5}}&\hline{\mathrm{4}}&\hline{\mathrm{5}}&\hline{\mathrm{4}}\\{{A}_{{n}} }&\hline{\mathrm{7}}&\hline{\mathrm{6}}&\hline{\mathrm{7}}&\hline{\mathrm{6}}&\hline{\mathrm{6}}&\hline{\mathrm{6}}&\hline{\mathrm{7}}&\hline{\mathrm{6}}&\hline{\mathrm{6}}&\hline{\mathrm{6}}&\hline{\mathrm{6}}\\{}&\hline{\mathrm{35}}&\hline{\mathrm{24}}&\hline{\mathrm{35}}&\hline{\mathrm{30}}&\hline{\mathrm{24}}&\hline{\mathrm{24}}&\hline{\mathrm{35}}&\hline{\mathrm{30}}&\hline{\mathrm{24}}&\hline{\mathrm{30}}&\hline{\mathrm{24}}\\\hline\end{array} \\ $$$$\mathrm{35}×\mathrm{3}+\mathrm{24}×\mathrm{5}+\mathrm{30}×\mathrm{3}=\mathrm{315} \\ $$$$ \\ $$$$\Rightarrow{totally}\:\mathrm{245}+\mathrm{315}=\mathrm{560}\:{numbers}\:{with}\: \\ $$$${different}\:{digits} \\ $$$$ \\ $$$$================ \\ $$$${explanation}\:{of}\:{the}\:{table} \\ $$$${say}\:{the}\:{number}\:{is}\:{ABCD}. \\ $$$${when}\:{CD}=\mathrm{08},\:{B}\:{can}\:{be}\:\mathrm{2},\:\mathrm{4},\:\mathrm{6},\:{i}.{e}. \\ $$$$\mathrm{3}\:{possibilities}\:\left({B}_{{n}} =\mathrm{3}\right).\:{for}\:{each}\:{B}=\mathrm{2}, \\ $$$${A}\:{can}\:{be}\:\mathrm{1},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{6},\mathrm{7},\mathrm{9},\:{i}.{e}.\:\mathrm{7}\:{possibilities} \\ $$$$\:\left({A}_{{n}} =\mathrm{7}\right).\:\Rightarrow\mathrm{3}×\mathrm{7}=\mathrm{21}\:{numbers}. \\ $$
Commented by Acem last updated on 16/Oct/22
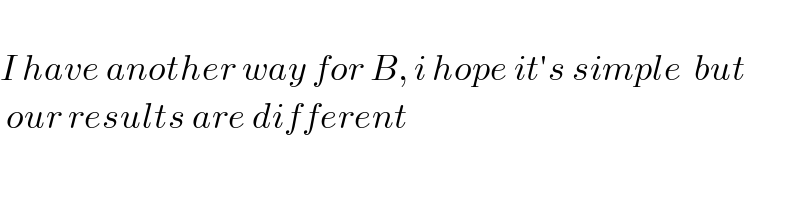
$$ \\ $$$${I}\:{have}\:{another}\:{way}\:{for}\:{B},\:{i}\:{hope}\:{it}'{s}\:{simple}\:\:{but} \\ $$$$\:{our}\:{results}\:{are}\:{different} \\ $$
Commented by Acem last updated on 16/Oct/22

$$\:{My}\:{answer}\:{for}\:{B}\:{is}\:\mathrm{541},\: \\ $$$$\:{There}\:{are}\:\mathrm{19}\:{diff}.\:{num}.\:{between}\:{us},\: \\ $$$$\:{The}\:{solution}\:{is}\:{below} \\ $$
Commented by mr W last updated on 16/Oct/22

$${please}\:{recheck}\:{your}\:{solution}\:{sir}. \\ $$$${the}\:{correct}\:{answer}\:{is}\:\mathrm{560}. \\ $$
Commented by Acem last updated on 17/Oct/22

$${Yes},\:{because}\:{one}\:{of}\:{the}\:{excluded}\:{numbers} \\ $$$$\:{i}\:{subtract}\:{it}\:{twice},\:{ooops}.\:{Anyway}\:{my}\:{method} \\ $$$$\:{is}\:{less}\:{difficult}\:{of}\:{yours}.\:{I}\:{tried}\:{yours}\:{and}\:{it} \\ $$$$\:{need}\:{for}\:{each}\:{CD}\:{must}\:{write}\:{or}\:{figure} \\ $$$$\:\mathrm{2}\:{subgroups}\:{for}\:{AB},\:{while}\:{mine}\:{need}\:{only} \\ $$$$\:{simply}\:{compensation}\:{values}\:{odd}\:\&\:{even}. \\ $$$$\:{Good}\:{luck}! \\ $$
Commented by mr W last updated on 18/Oct/22
$${i}\:{never}\:{praise}\:{myself}. \\ $$
Commented by Acem last updated on 18/Oct/22

$${You}\:{do}\:{indirectly}.\:{But}\:{me}\:{never}.\: \\ $$$$ \\ $$$${Anyway}\:{i}\:{said}\:{that}\:{my}\:{method}\:{is}\:{easier}\:{not}\:{to} \\ $$$$\:{praise}\:{myself}\:``{didn}'{t}\:{talk}\:{my}\:{skin}\:{color}'',\:{but} \\ $$$$\:{for}\:{all}\:{of}\:{us}\:{to}\:{usefull}\:{from}\:{each}\:{other}, \\ $$$$\:{and}\:{take}\:{from}\:{all}\:{the}\:{better}\:{idea},\:{especially}\:{the} \\ $$$$\:{easier},\:{whatever}\:{whose}! \\ $$$$ \\ $$$${By}\:{the}\:{way}_{\mathrm{1}} \:{our}\:{methods}\:{and}\:{ideas}\:{about}\: \\ $$$$\:{this}\:{qusetion}\:{are}\:{very}\:{close} \\ $$$$ \\ $$$${By}\:{the}\:{way}_{\mathrm{2}} \:{when}\:{i}\:{composed}\:{this}\:{question} \\ $$$$\:{i}\:{was}\:{sure}\:{that}\:{you}\:{will}\:{like}\:{it}\:{and} \\ $$$$\:\boldsymbol{{solve}}\:\boldsymbol{{it}}\:\boldsymbol{{correctly}}. \\ $$$$ \\ $$$${Sincerely} \\ $$$$\: \\ $$$$ \\ $$
Answered by Acem last updated on 19/Oct/22

$$ \\ $$$$\:\boldsymbol{{A}}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Last}\:\:\:\:\:\:\:\:{two}\:\:\:\:\:\:\:\:\:{digits} \\ $$$$\begin{array}{|c|c|c|c|c|c|}{{T}_{{th}} }&\hline{\:\boldsymbol{{Th}}}&\hline{}&\hline{}&\hline{}&\hline{}&\hline{}&\hline{}&\hline{{n}}&\hline{}\\{\mathrm{1}}&\hline{\:\:\:\mathrm{0}^{{ev}} }&\hline{\mathrm{00}}&\hline{\mathrm{08}}&\hline{\mathrm{16}}&\hline{...}&\hline{\mathrm{88}}&\hline{\mathrm{96}}&\hline{\mathrm{13}}&\hline{{even}_{{Th}} }\\{\mathrm{2}}&\hline{\:\:\:\mathrm{1}^{{odd}} }&\hline{\mathrm{04}}&\hline{\mathrm{12}}&\hline{\mathrm{20}}&\hline{...}&\hline{\mathrm{84}}&\hline{\mathrm{92}}&\hline{\mathrm{12}}&\hline{{odd}_{{Th}} }\\{\mathrm{3}}&\hline{\:\:\:\mathrm{2}^{{ev}} }&\hline{}&\hline{}&\hline{}&\hline{...}&\hline{}&\hline{}&\hline{\mathrm{13}}&\hline{{even}_{{Th}} }\\{\vdots}&\hline{\:\:\vdots}&\hline{}&\hline{}&\hline{}&\hline{}&\hline{}&\hline{}&\hline{}&\hline{}\\{\mathrm{9}}&\hline{\:\:\:\mathrm{9}^{{odd}} }&\hline{\mathrm{04}}&\hline{\mathrm{12}}&\hline{\mathrm{20}}&\hline{...}&\hline{\mathrm{84}}&\hline{\mathrm{92}}&\hline{\mathrm{12}}&\hline{{odd}_{{Th}} }\\\hline\end{array} \\ $$$$\begin{array}{|c|c|}{{The}\:\mathrm{2}{dig}_{{Th}} .\:{has}\:\mathrm{5}_{{even}} \&\:\mathrm{5}_{{odd}} }\\{\mathrm{9}_{{T}_{{th}} } ×\mathrm{5}_{{even}} ×\mathrm{13}\:+\:\mathrm{9}_{{T}_{{th}} } ×\mathrm{5}_{{odd}} ×\mathrm{12}}\\\hline\end{array} \\ $$$$ \\ $$$$\:{NumNumb}._{{divisible}\:{by}\:\:\mathrm{8}} \:=\:\mathrm{9}×\mathrm{5}\left(\mathrm{13}+\mathrm{12}\right)=\:\mathrm{1}\:\mathrm{125} \\ $$$$\:\boldsymbol{{Note}}:\:{This}\:{method}\:{is}\:{for}\:{who}\:{didn}'{t}\:{get}\:{the} \\ $$$$\:{two}\:{methods}\:{above}.\:{And}\:{it}'{s}\:{usefull}\:{for}\:{next}\:\left({B}\right) \\ $$$$ \\ $$$$\:{B}:\:{is}\:{next}\:{soon} \\ $$$$ \\ $$
Commented by Acem last updated on 16/Oct/22

$${Good}\:{Sir}!\:\:{as}\:{you}\:{said}\:{it}'{s}\:{easy},\:{but}\:{it}\:{might}\:{not} \\ $$$$\:{come}\:{to}\:{mind} \\ $$
Answered by Acem last updated on 19/Oct/22

$$ \\ $$$$\:\boldsymbol{{B}}: \\ $$$$\:{NumNumb}._{{divis}.\:{by}\:\:\mathrm{8},\:{diff}.{dig}} =\:\:{N}_{{even}_{{Th}} } +\:{N}_{{odd}_{{Th}} } ...\left(\mathrm{1}\right) \\ $$$$\:{N}_{{even}_{{Th}} } \:;\:{last}\:{two}\:{dig}\:{are}:\:\mathrm{00},\:\mathrm{08},\:\mathrm{16},\:\mathrm{24},\:...,\:\mathrm{88},\:\mathrm{96} \\ $$$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}{}&\hline{\boldsymbol{{even}}}\\{{T}_{{Th}} }&\hline{{Th}}\\{\mathrm{1}^{\smile\mathrm{5}} }&\hline{\mathrm{0}^{\smile\mathrm{9}} }\\{\mathrm{2}^{\smile\mathrm{4}} }&\hline{\mathrm{2}^{\smile\mathrm{8}} }\\{\mathrm{3}}&\hline{\mathrm{4}}\\{\mathrm{4}}&\hline{\mathrm{6}}\\{\mathrm{5}}&\hline{\mathrm{8}^{\smile\mathrm{8}} }\\{\mathrm{6}}&\hline{}\\{\mathrm{7}}&\hline{}\\{\mathrm{8}}&\hline{}\\{\mathrm{9}}&\hline{}\\\hline\end{array}{N}_{{two}\:\mathrm{1}{st}\:{dig}} =\:\mathrm{5}_{{odd}} ×\mathrm{5}^{{Th}} +\mathrm{4}_{{even}} ×\mathrm{4}^{{Th}} =\:\mathrm{41} \\ $$$$\:\boldsymbol{{Tips}}: \\ $$$$\:\mathrm{0}:\:{must}\:{subtract}\:\mathrm{9} \\ $$$$\:{even}:\:{must}\:{subtract}\:\mathrm{11}_{{To}\:{figure}\:{how}\:{i}\:{said}\:\mathrm{11}} ^{{Try}\:{making}\:{a}\:{num}.\:{xy\_}\mathrm{08}} \\ $$$$\:{odd}:\:{must}\:{subtract}\:\mathrm{5} \\ $$$$\:{xx}:\:{is}\:{not}\:{valid},\:{must}\:{subtract}\:\mathrm{41} \\ $$$$\:\mathrm{08}:\:\mathrm{9}+\mathrm{11}\Rightarrow\mathrm{20},\:\mathrm{32}\Rightarrow\:\mathrm{16},\:\mathrm{48}\Rightarrow\mathrm{22}...{etc} \\ $$$$ \\ $$$$\begin{array}{|c|c|}{}&\hline{\mathrm{00}}&\hline{\mathrm{08}}&\hline{\mathrm{16}}&\hline{\mathrm{24}}&\hline{\mathrm{32}}&\hline{\mathrm{40}}&\hline{\mathrm{48}}&\hline{\mathrm{56}}&\hline{\mathrm{64}}&\hline{\mathrm{72}}&\hline{\mathrm{80}}&\hline{\mathrm{88}}&\hline{\mathrm{96}}&\hline{{n}=\mathrm{13}}\\{{Sum}}&\hline{\mathrm{41}}&\hline{\mathrm{20}}&\hline{\mathrm{16}}&\hline{\mathrm{22}}&\hline{\mathrm{16}}&\hline{\mathrm{20}}&\hline{\mathrm{22}}&\hline{\mathrm{16}}&\hline{\mathrm{22}}&\hline{\mathrm{16}}&\hline{\mathrm{20}}&\hline{\mathrm{41}}&\hline{\mathrm{16}}&\hline{}\\\hline\end{array} \\ $$$$\:{Sum}=\:\mathrm{41}×\mathrm{2}+\:\mathrm{20}×\mathrm{3}+\:\mathrm{16}×\mathrm{5}+\:\mathrm{22}×\mathrm{3}=\:\mathrm{288} \\ $$$${N}_{{even}_{{Th}} } =\:\mathrm{41}×\mathrm{13}−\mathrm{288}=\:\mathrm{245}\:...\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\:{N}_{{odd}_{{Th}} } \:;\:{last}\:{two}\:{dig}\:{are}:\:\mathrm{04},\:\mathrm{12},\:\mathrm{20},\:\mathrm{28},\:...,\:\mathrm{84},\:\mathrm{92} \\ $$$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}{}&\hline{\boldsymbol{{odd}}}\\{{T}_{{Th}} }&\hline{{Th}}\\{\mathrm{1}^{\smile\mathrm{4}} }&\hline{\mathrm{1}^{\smile\mathrm{8}} }\\{\mathrm{2}^{\smile\mathrm{5}} }&\hline{\mathrm{3}^{\smile\mathrm{8}} }\\{\mathrm{3}}&\hline{\mathrm{5}}\\{\mathrm{4}}&\hline{\mathrm{7}}\\{\mathrm{5}}&\hline{\mathrm{9}^{\smile\mathrm{8}} }\\{\mathrm{6}}&\hline{}\\{\mathrm{7}}&\hline{}\\{\mathrm{8}}&\hline{}\\{\mathrm{9}}&\hline{}\\\hline\end{array}{N}_{{two}\:\mathrm{1}{st}\:{dig}} =\:\mathrm{5}_{{odd}} ×\mathrm{4}^{{Th}} +\mathrm{4}_{{even}} ×\mathrm{5}^{{Th}} =\:\mathrm{40} \\ $$$$\:\boldsymbol{{Tips}}: \\ $$$$\:{even}:\:{must}\:{subtract}\:\mathrm{5} \\ $$$$\:{odd}:\:{must}\:{subtract}\:\mathrm{11} \\ $$$$\:{xx}:\:{is}\:{not}\:{valid},\:{must}\:{subtract}\:\mathrm{40} \\ $$$$\begin{array}{|c|c|}{}&\hline{\mathrm{04}}&\hline{\mathrm{12}}&\hline{\mathrm{20}}&\hline{\mathrm{28}}&\hline{\mathrm{36}}&\hline{\mathrm{44}}&\hline{\mathrm{52}}&\hline{\mathrm{60}}&\hline{\mathrm{68}}&\hline{\mathrm{76}}&\hline{\mathrm{84}}&\hline{\mathrm{92}}&\hline{{n}=\mathrm{12}}\\{{Sum}}&\hline{\mathrm{5}}&\hline{\mathrm{16}}&\hline{\mathrm{5}}&\hline{\mathrm{10}}&\hline{\mathrm{16}}&\hline{\mathrm{40}}&\hline{\mathrm{16}}&\hline{\mathrm{5}}&\hline{\mathrm{10}}&\hline{\mathrm{16}}&\hline{\mathrm{10}}&\hline{\mathrm{16}}&\hline{}\\\hline\end{array} \\ $$$${Sum}=\:\mathrm{5}×\mathrm{3}+\:\mathrm{16}×\mathrm{5}+\:\mathrm{10}×\mathrm{3}+\:\mathrm{40}×\mathrm{1}=\:\mathrm{165} \\ $$$${N}_{{odd}_{{Th}} } =\:\mathrm{40}×\mathrm{12}−\mathrm{165}=\:\mathrm{315}\:...\left(\mathrm{3}\right) \\ $$$$ \\ $$$$\:{By}\:{compensate}\:\left(\mathrm{2}\right)\:\&\:\left(\mathrm{3}\right)\:{in}\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$${NumNumb}._{{divis}.\:{by}\:\:\mathrm{8},\:{diff}.{dig}} =\:\mathrm{245}+\:\mathrm{315}=\:\mathrm{560} \\ $$$$ \\ $$
