Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 178354 by Spillover last updated on 15/Oct/22

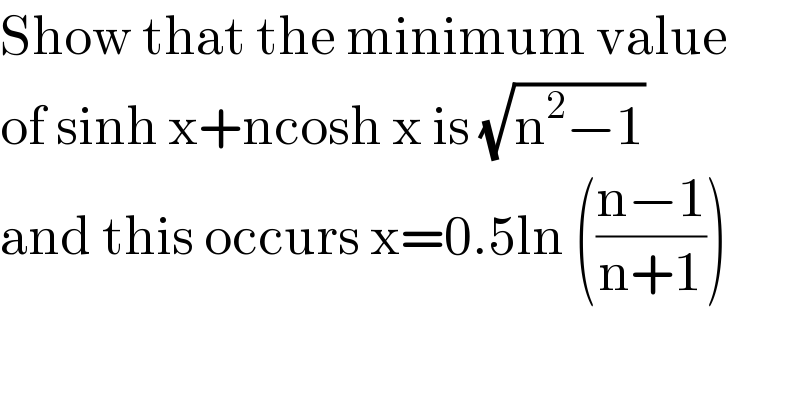
Show that the minimum value of sinh x+ncosh x is (√(n^2 −1)) and this occurs x=0.5ln (((n−1)/(n+1)))

$$\mathrm{Show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{value} \\ $$$$\mathrm{of}\:\mathrm{sinh}\:\mathrm{x}+\mathrm{ncosh}\:\mathrm{x}\:\mathrm{is}\:\sqrt{\mathrm{n}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\mathrm{and}\:\mathrm{this}\:\mathrm{occurs}\:\mathrm{x}=\mathrm{0}.\mathrm{5ln}\:\left(\frac{\mathrm{n}−\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right) \\ $$

Answered by Ar Brandon last updated on 16/Oct/22

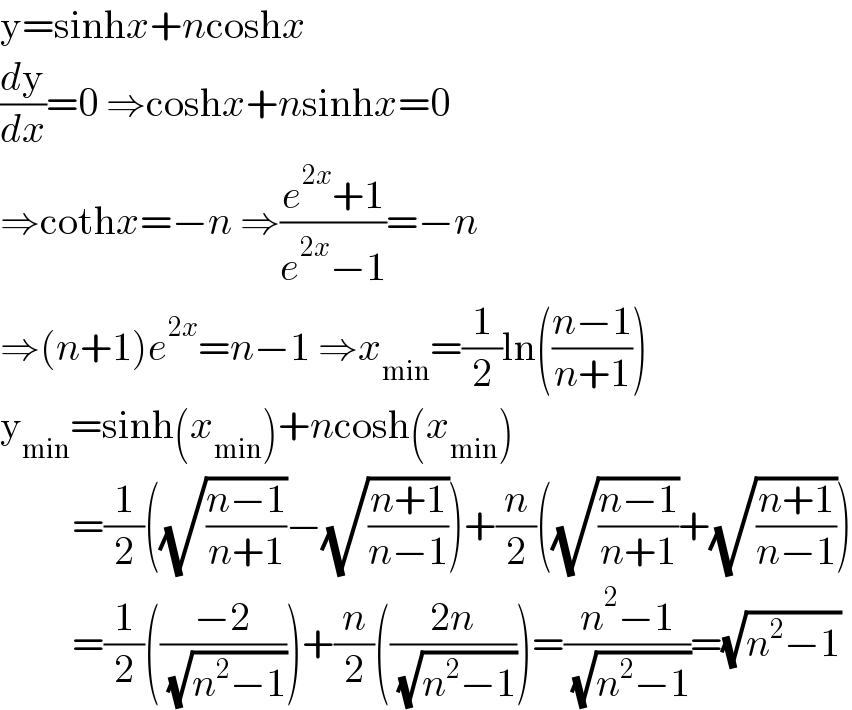
y=sinhx+ncoshx (dy/dx)=0 ⇒coshx+nsinhx=0 ⇒cothx=−n ⇒((e^(2x) +1)/(e^(2x) −1))=−n ⇒(n+1)e^(2x) =n−1 ⇒x_(min) =(1/2)ln(((n−1)/(n+1))) y_(min) =sinh(x_(min) )+ncosh(x_(min) ) =(1/2)((√((n−1)/(n+1)))−(√((n+1)/(n−1))))+(n/2)((√((n−1)/(n+1)))+(√((n+1)/(n−1)))) =(1/2)(((−2)/( (√(n^2 −1)))))+(n/2)(((2n)/( (√(n^2 −1)))))=((n^2 −1)/( (√(n^2 −1))))=(√(n^2 −1))

$$\mathrm{y}=\mathrm{sinh}{x}+{n}\mathrm{cosh}{x} \\ $$$$\frac{{d}\mathrm{y}}{{dx}}=\mathrm{0}\:\Rightarrow\mathrm{cosh}{x}+{n}\mathrm{sinh}{x}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{coth}{x}=−{n}\:\Rightarrow\frac{{e}^{\mathrm{2}{x}} +\mathrm{1}}{{e}^{\mathrm{2}{x}} −\mathrm{1}}=−{n} \\ $$$$\Rightarrow\left({n}+\mathrm{1}\right){e}^{\mathrm{2}{x}} ={n}−\mathrm{1}\:\Rightarrow{x}_{\mathrm{min}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{{n}−\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$\mathrm{y}_{\mathrm{min}} =\mathrm{sinh}\left({x}_{\mathrm{min}} \right)+{n}\mathrm{cosh}\left({x}_{\mathrm{min}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\frac{{n}−\mathrm{1}}{{n}+\mathrm{1}}}−\sqrt{\frac{{n}+\mathrm{1}}{{n}−\mathrm{1}}}\right)+\frac{{n}}{\mathrm{2}}\left(\sqrt{\frac{{n}−\mathrm{1}}{{n}+\mathrm{1}}}+\sqrt{\frac{{n}+\mathrm{1}}{{n}−\mathrm{1}}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{−\mathrm{2}}{\:\sqrt{{n}^{\mathrm{2}} −\mathrm{1}}}\right)+\frac{{n}}{\mathrm{2}}\left(\frac{\mathrm{2}{n}}{\:\sqrt{{n}^{\mathrm{2}} −\mathrm{1}}}\right)=\frac{{n}^{\mathrm{2}} −\mathrm{1}}{\:\sqrt{{n}^{\mathrm{2}} −\mathrm{1}}}=\sqrt{{n}^{\mathrm{2}} −\mathrm{1}} \\ $$

Commented by Spillover last updated on 16/Oct/22

thanks

$${thanks} \\ $$

Commented by Spillover last updated on 17/Oct/22

please explain the second line from the end.

$$\mathrm{please}\:\mathrm{explain}\:\mathrm{the}\:\mathrm{second}\:\mathrm{line} \\ $$$$\mathrm{from}\:\mathrm{the}\:\mathrm{end}. \\ $$

Commented by Ar Brandon last updated on 17/Oct/22

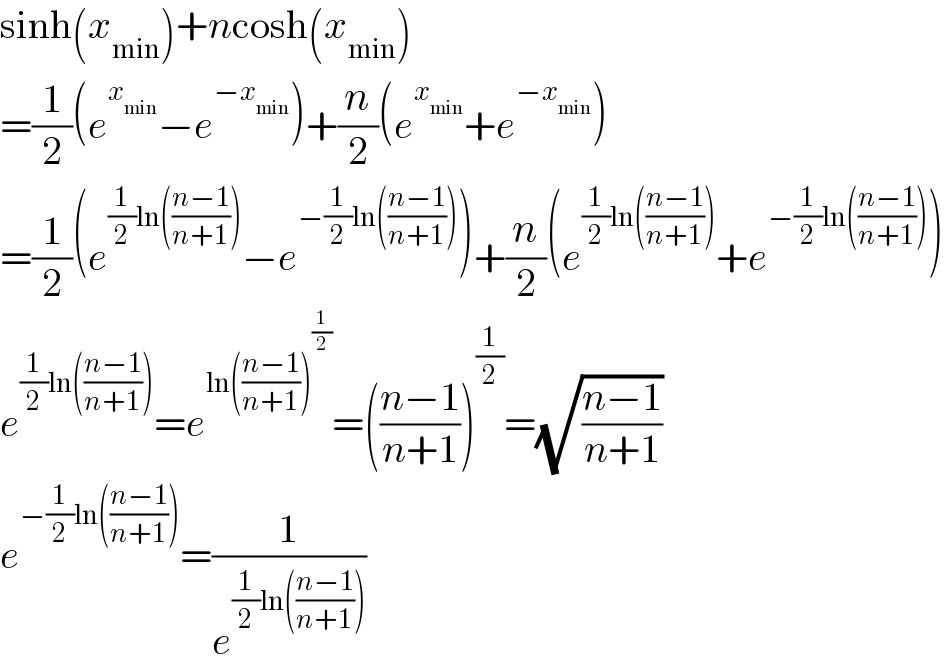
sinh(x_(min) )+ncosh(x_(min) ) =(1/2)(e^x_(min) −e^(−x_(min) ) )+(n/2)(e^x_(min) +e^(−x_(min) ) ) =(1/2)(e^((1/2)ln(((n−1)/(n+1)))) −e^(−(1/2)ln(((n−1)/(n+1)))) )+(n/2)(e^((1/2)ln(((n−1)/(n+1)))) +e^(−(1/2)ln(((n−1)/(n+1)))) ) e^((1/2)ln(((n−1)/(n+1)))) =e^(ln(((n−1)/(n+1)))^(1/2) ) =(((n−1)/(n+1)))^(1/2) =(√((n−1)/(n+1))) e^(−(1/2)ln(((n−1)/(n+1)))) =(1/e^((1/2)ln(((n−1)/(n+1)))) )

$$\mathrm{sinh}\left({x}_{\mathrm{min}} \right)+{n}\mathrm{cosh}\left({x}_{\mathrm{min}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({e}^{{x}_{\mathrm{min}} } −{e}^{−{x}_{\mathrm{min}} } \right)+\frac{{n}}{\mathrm{2}}\left({e}^{{x}_{\mathrm{min}} } +{e}^{−{x}_{\mathrm{min}} } \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({e}^{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{{n}−\mathrm{1}}{{n}+\mathrm{1}}\right)} −{e}^{−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{{n}−\mathrm{1}}{{n}+\mathrm{1}}\right)} \right)+\frac{{n}}{\mathrm{2}}\left({e}^{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{{n}−\mathrm{1}}{{n}+\mathrm{1}}\right)} +{e}^{−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{{n}−\mathrm{1}}{{n}+\mathrm{1}}\right)} \right) \\ $$$${e}^{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{{n}−\mathrm{1}}{{n}+\mathrm{1}}\right)} ={e}^{\mathrm{ln}\left(\frac{{n}−\mathrm{1}}{{n}+\mathrm{1}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} } =\left(\frac{{n}−\mathrm{1}}{{n}+\mathrm{1}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\sqrt{\frac{{n}−\mathrm{1}}{{n}+\mathrm{1}}} \\ $$$${e}^{−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{{n}−\mathrm{1}}{{n}+\mathrm{1}}\right)} =\frac{\mathrm{1}}{{e}^{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{{n}−\mathrm{1}}{{n}+\mathrm{1}}\right)} } \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com