
Question and Answers Forum
Question Number 178487 by cortano1 last updated on 17/Oct/22
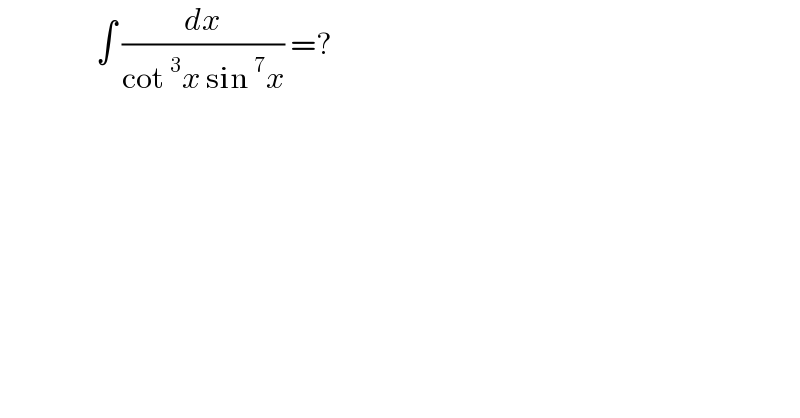
Answered by Frix last updated on 18/Oct/22

Answered by Ar Brandon last updated on 17/Oct/22

Answered by greougoury555 last updated on 18/Oct/22
![let s=sin x I= ∫ (ds/((1−s^2 )^2 s^4 )) =∫ (ds/(((1−s^2 )s^2 )^2 )) Partial fractions (1/([(1−s^2 )s^2 ]^2 )) = ((1/(1−s^2 )) +(1/s^2 ))^2 = ((1/(1−s^2 )))^2 +(2/((1−s^2 )s^2 )) +(1/s^4 ) = [ (1/2)((1/(1−s)) +(1/(1+s)))]^2 +(2/(1−s^2 )) +(2/s^2 )+(1/s^4 ) = (1/(4(1−s)^2 )) +(5/(2(1−s^2 )))+(1/(4(1+s)^2 ))+(2/s^2 )+(1/s^4 ) I=∫ (ds/((1−s^2 )^2 s^4 )) = ∫ [ (1/(4(1−s)^2 )) +(5/(2(1−s^2 )))+(1/(4(1+s)^2 ))+(2/s^2 )+(1/s^4 ) ]ds = (1/(4(1−s)))+(5/4) ln ∣((1+s)/(1−s)) ∣−(1/(4(1+s)))−(2/s)−(1/(3s^3 )) +c = (1/(4(1−sin x))) +(5/4) ln ∣((1+sin x)/(1−sin x))∣−(1/(4(1+sin x)))−(2/(sin x))−(1/(3sin^3 x)) + c](Q178555.png)
| ||
Question and Answers Forum | ||
Question Number 178487 by cortano1 last updated on 17/Oct/22 | ||
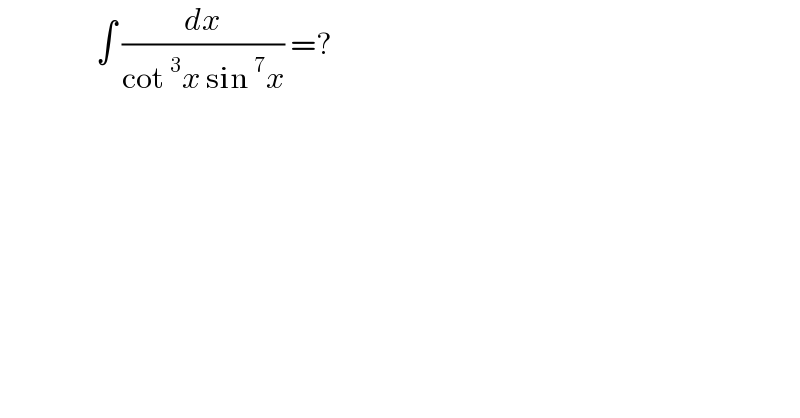 | ||
Answered by Frix last updated on 18/Oct/22 | ||
 | ||
| ||
Answered by Ar Brandon last updated on 17/Oct/22 | ||
 | ||
| ||
Answered by greougoury555 last updated on 18/Oct/22 | ||
![let s=sin x I= ∫ (ds/((1−s^2 )^2 s^4 )) =∫ (ds/(((1−s^2 )s^2 )^2 )) Partial fractions (1/([(1−s^2 )s^2 ]^2 )) = ((1/(1−s^2 )) +(1/s^2 ))^2 = ((1/(1−s^2 )))^2 +(2/((1−s^2 )s^2 )) +(1/s^4 ) = [ (1/2)((1/(1−s)) +(1/(1+s)))]^2 +(2/(1−s^2 )) +(2/s^2 )+(1/s^4 ) = (1/(4(1−s)^2 )) +(5/(2(1−s^2 )))+(1/(4(1+s)^2 ))+(2/s^2 )+(1/s^4 ) I=∫ (ds/((1−s^2 )^2 s^4 )) = ∫ [ (1/(4(1−s)^2 )) +(5/(2(1−s^2 )))+(1/(4(1+s)^2 ))+(2/s^2 )+(1/s^4 ) ]ds = (1/(4(1−s)))+(5/4) ln ∣((1+s)/(1−s)) ∣−(1/(4(1+s)))−(2/s)−(1/(3s^3 )) +c = (1/(4(1−sin x))) +(5/4) ln ∣((1+sin x)/(1−sin x))∣−(1/(4(1+sin x)))−(2/(sin x))−(1/(3sin^3 x)) + c](Q178555.png) | ||
| ||