Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 178577 by Spillover last updated on 18/Oct/22

prove that (a)cosh^(−1) x=±ln (x+(√(x^2 −1))) (b)tanh^(−1) x=(1/2)ln (((x+1)/(x−1))),∣x∣<1

$$\mathrm{prove}\:\mathrm{that} \\ $$ $$\left(\mathrm{a}\right)\mathrm{cosh}\:^{−\mathrm{1}} \mathrm{x}=\pm\mathrm{ln}\:\left(\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$ $$\left(\mathrm{b}\right)\mathrm{tanh}\:^{−\mathrm{1}} \mathrm{x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right),\mid\mathrm{x}\mid<\mathrm{1} \\ $$

Answered by depressiveshrek last updated on 18/Oct/22

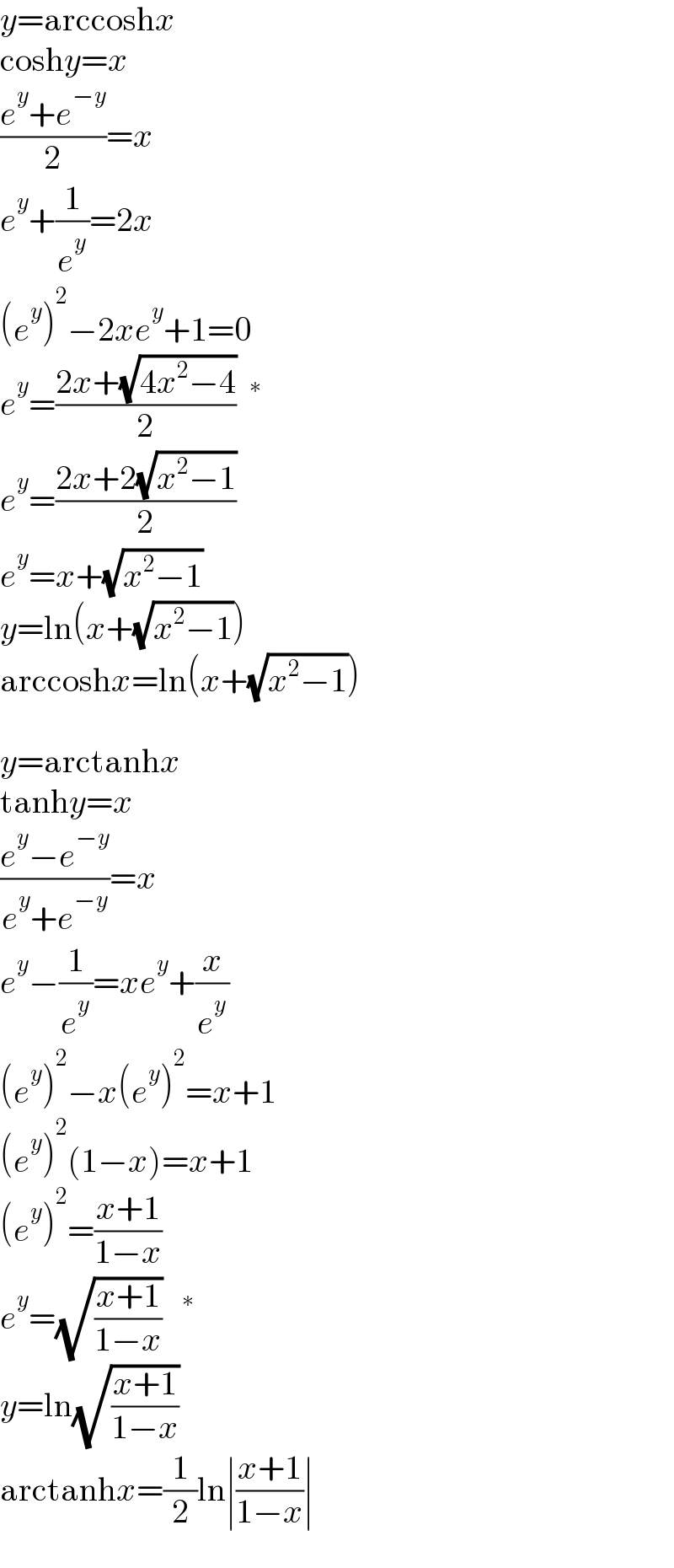
y=arccoshx coshy=x ((e^y +e^(−y) )/2)=x e^y +(1/e^y )=2x (e^y )^2 −2xe^y +1=0 e^y =((2x+(√(4x^2 −4)))/2) ^∗ e^y =((2x+2(√(x^2 −1)))/2) e^y =x+(√(x^2 −1)) y=ln(x+(√(x^2 −1))) arccoshx=ln(x+(√(x^2 −1))) y=arctanhx tanhy=x ((e^y −e^(−y) )/(e^y +e^(−y) ))=x e^y −(1/e^y )=xe^y +(x/e^y ) (e^y )^2 −x(e^y )^2 =x+1 (e^y )^2 (1−x)=x+1 (e^y )^2 =((x+1)/(1−x)) e^y =(√((x+1)/(1−x))) ^∗ y=ln(√((x+1)/(1−x))) arctanhx=(1/2)ln∣((x+1)/(1−x))∣

$${y}=\mathrm{arccosh}{x} \\ $$ $$\mathrm{cosh}{y}={x} \\ $$ $$\frac{{e}^{{y}} +{e}^{−{y}} }{\mathrm{2}}={x} \\ $$ $${e}^{{y}} +\frac{\mathrm{1}}{{e}^{{y}} }=\mathrm{2}{x} \\ $$ $$\left({e}^{{y}} \right)^{\mathrm{2}} −\mathrm{2}{xe}^{{y}} +\mathrm{1}=\mathrm{0} \\ $$ $${e}^{{y}} =\frac{\mathrm{2}{x}+\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}\:\:^{\ast} \\ $$ $${e}^{{y}} =\frac{\mathrm{2}{x}+\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{2}} \\ $$ $${e}^{{y}} ={x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$ $${y}=\mathrm{ln}\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$ $$\mathrm{arccosh}{x}=\mathrm{ln}\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$ $$\: \\ $$ $${y}=\mathrm{arctanh}{x} \\ $$ $$\mathrm{tanh}{y}={x} \\ $$ $$\frac{{e}^{{y}} −{e}^{−{y}} }{{e}^{{y}} +{e}^{−{y}} }={x} \\ $$ $${e}^{{y}} −\frac{\mathrm{1}}{{e}^{{y}} }={xe}^{{y}} +\frac{{x}}{{e}^{{y}} } \\ $$ $$\left({e}^{{y}} \right)^{\mathrm{2}} −{x}\left({e}^{{y}} \right)^{\mathrm{2}} ={x}+\mathrm{1} \\ $$ $$\left({e}^{{y}} \right)^{\mathrm{2}} \left(\mathrm{1}−{x}\right)={x}+\mathrm{1} \\ $$ $$\left({e}^{{y}} \right)^{\mathrm{2}} =\frac{{x}+\mathrm{1}}{\mathrm{1}−{x}} \\ $$ $${e}^{{y}} =\sqrt{\frac{{x}+\mathrm{1}}{\mathrm{1}−{x}}}\:\:\:^{\ast} \\ $$ $${y}=\mathrm{ln}\sqrt{\frac{{x}+\mathrm{1}}{\mathrm{1}−{x}}} \\ $$ $$\mathrm{arctanh}{x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{{x}+\mathrm{1}}{\mathrm{1}−{x}}\mid \\ $$

Commented bySpillover last updated on 18/Oct/22

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com