
Question Number 178785 by Mastermind last updated on 21/Oct/22

Answered by Rasheed.Sindhi last updated on 21/Oct/22
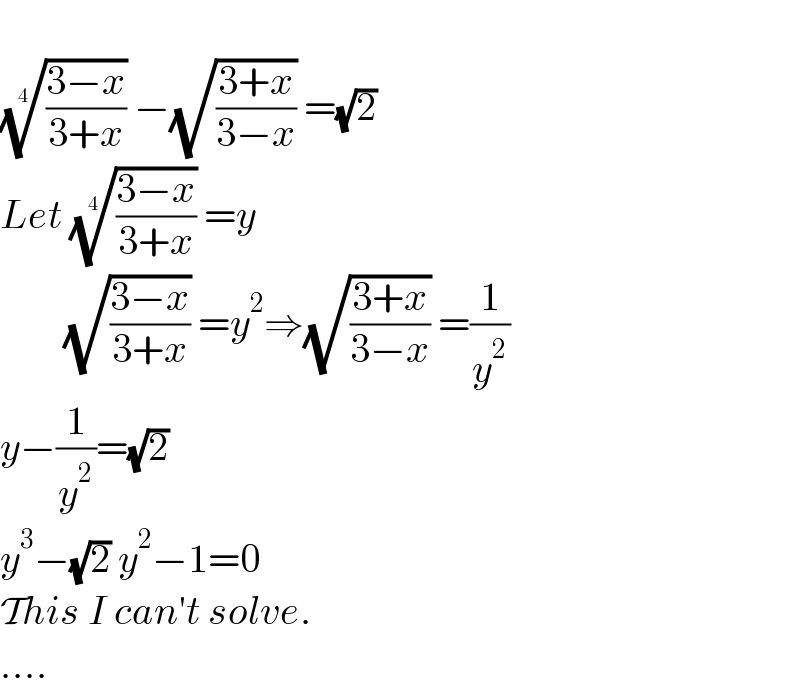
$$ \\ $$$$\sqrt[{\mathrm{4}}]{\frac{\mathrm{3}−{x}}{\mathrm{3}+{x}}}\:−\sqrt{\frac{\mathrm{3}+{x}}{\mathrm{3}−{x}}}\:=\sqrt{\mathrm{2}} \\ $$$${Let}\:\sqrt[{\mathrm{4}}]{\frac{\mathrm{3}−{x}}{\mathrm{3}+{x}}}\:={y} \\ $$$$\:\:\:\:\:\:\:\:\sqrt{\frac{\mathrm{3}−{x}}{\mathrm{3}+{x}}}\:={y}^{\mathrm{2}} \Rightarrow\sqrt{\frac{\mathrm{3}+{x}}{\mathrm{3}−{x}}}\:=\frac{\mathrm{1}}{{y}^{\mathrm{2}} } \\ $$$${y}−\frac{\mathrm{1}}{{y}^{\mathrm{2}} }=\sqrt{\mathrm{2}} \\ $$$${y}^{\mathrm{3}} −\sqrt{\mathrm{2}}\:{y}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\mathcal{T}{his}\:{I}\:{can}'{t}\:{solve}. \\ $$$$.... \\ $$
Commented by cortano1 last updated on 21/Oct/22

$$\mathrm{typo}\:.\:\mathrm{it}'\mathrm{s}\:\sqrt[{\mathrm{4}}]{\frac{\mathrm{3}−\mathrm{x}}{\mathrm{3}+\mathrm{x}}} \\ $$
Commented by Rasheed.Sindhi last updated on 21/Oct/22

$$\mathcal{T}{han}\mathcal{X}\:{sir},\:{corrected}! \\ $$
Commented by mr W last updated on 21/Oct/22
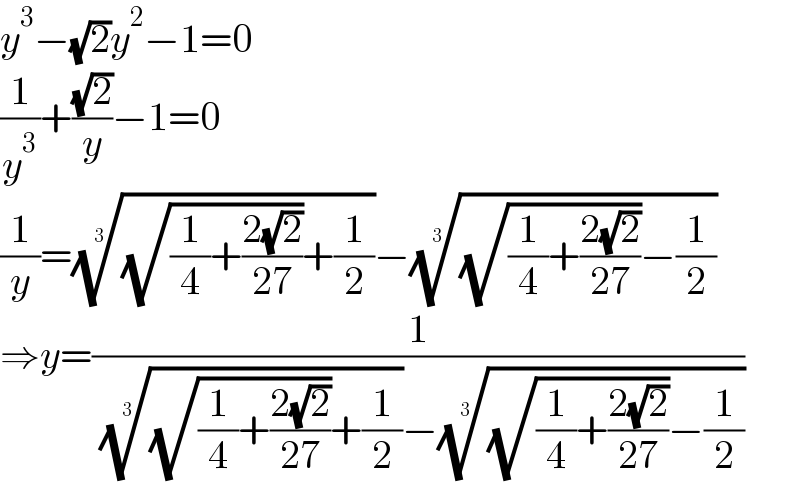
$${y}^{\mathrm{3}} −\sqrt{\mathrm{2}}{y}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{y}^{\mathrm{3}} }+\frac{\sqrt{\mathrm{2}}}{{y}}−\mathrm{1}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{y}}=\sqrt[{\mathrm{3}}]{\sqrt{\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{27}}}+\frac{\mathrm{1}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\sqrt{\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{27}}}−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\Rightarrow{y}=\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\sqrt{\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{27}}}+\frac{\mathrm{1}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\sqrt{\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{27}}}−\frac{\mathrm{1}}{\mathrm{2}}}} \\ $$
Commented by Spillover last updated on 21/Oct/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
