Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 178793 by infinityaction last updated on 21/Oct/22

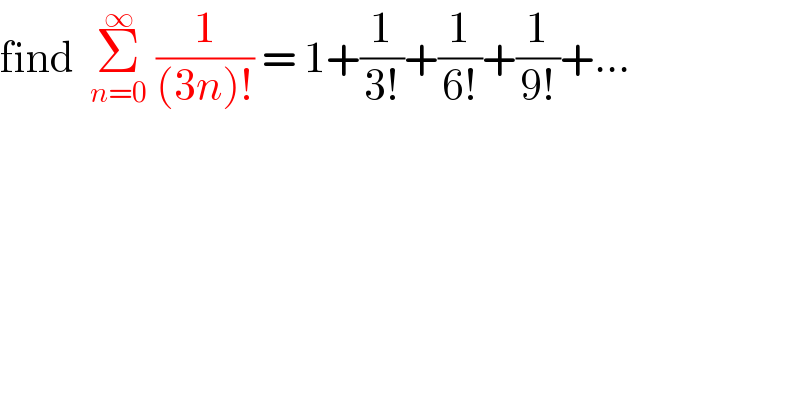
find Σ_(n=0) ^∞ (1/((3n)!)) = 1+(1/(3!))+(1/(6!))+(1/(9!))+...

$$\mathrm{find}\:\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\left(\mathrm{3}{n}\right)!}\:=\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{6}!}+\frac{\mathrm{1}}{\mathrm{9}!}+... \\ $$

Answered by aleks041103 last updated on 21/Oct/22

w=e^((2πi)/3) ⇒w^2 =w^∗ ,w^3 =1 e^w =Σ_(n=0) ^∞ (1/((3n)!))+(w/((3n+1)!))+(w^2 /((3n+2)!))=S_0 +wS_1 +w^2 S_2 e^w^2 =Σ_(n=0) ^∞ (1/((3n)!))+(w^2 /((3n+1)!))+(w/((3n+2)!))=S_0 +w^2 S_1 +wS_2 e^1 =S_0 +S_1 +S_2 e^w +e^w^2 −2e=(w+w^2 −2)(S_1 +S_2 )=−3(S_1 +S_2 ) ⇒S_0 =e−(S_1 +S_2 )=e+(((exp(w)+exp(w^2 )−2e))/3)= =((e^1 +e^w +e^w^2 )/3)=S_0 w=e^((2πi)/3) =−(1/2)+i((√3)/2) w^2 =e^(−((2πi)/3)) =−(1/2)−i((√3)/2) ⇒e^w =(1/( (√e)))e^(i(√3)/2) ,e^w^2 =(1/( (√e)))e^(−i(√3)/2) ⇒e^w +e^w^2 =(2/( (√e)))cos(((√3)/2)) ⇒Σ_(n=0) ^∞ (1/((3n)!))=(e/3)+(2/(3(√e)))cos((√3)/2)

$${w}={e}^{\frac{\mathrm{2}\pi{i}}{\mathrm{3}}} \Rightarrow{w}^{\mathrm{2}} ={w}^{\ast} ,{w}^{\mathrm{3}} =\mathrm{1} \\ $$$${e}^{{w}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{n}\right)!}+\frac{{w}}{\left(\mathrm{3}{n}+\mathrm{1}\right)!}+\frac{{w}^{\mathrm{2}} }{\left(\mathrm{3}{n}+\mathrm{2}\right)!}={S}_{\mathrm{0}} +{wS}_{\mathrm{1}} +{w}^{\mathrm{2}} {S}_{\mathrm{2}} \\ $$$${e}^{{w}^{\mathrm{2}} } =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{n}\right)!}+\frac{{w}^{\mathrm{2}} }{\left(\mathrm{3}{n}+\mathrm{1}\right)!}+\frac{{w}}{\left(\mathrm{3}{n}+\mathrm{2}\right)!}={S}_{\mathrm{0}} +{w}^{\mathrm{2}} {S}_{\mathrm{1}} +{wS}_{\mathrm{2}} \\ $$$${e}^{\mathrm{1}} ={S}_{\mathrm{0}} +{S}_{\mathrm{1}} +{S}_{\mathrm{2}} \\ $$$${e}^{{w}} +{e}^{{w}^{\mathrm{2}} } −\mathrm{2}{e}=\left({w}+{w}^{\mathrm{2}} −\mathrm{2}\right)\left({S}_{\mathrm{1}} +{S}_{\mathrm{2}} \right)=−\mathrm{3}\left({S}_{\mathrm{1}} +{S}_{\mathrm{2}} \right) \\ $$$$\Rightarrow{S}_{\mathrm{0}} ={e}−\left({S}_{\mathrm{1}} +{S}_{\mathrm{2}} \right)={e}+\frac{\left({exp}\left({w}\right)+{exp}\left({w}^{\mathrm{2}} \right)−\mathrm{2}{e}\right)}{\mathrm{3}}= \\ $$$$=\frac{{e}^{\mathrm{1}} +{e}^{{w}} +{e}^{{w}^{\mathrm{2}} } }{\mathrm{3}}={S}_{\mathrm{0}} \\ $$$${w}={e}^{\frac{\mathrm{2}\pi{i}}{\mathrm{3}}} =−\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${w}^{\mathrm{2}} ={e}^{−\frac{\mathrm{2}\pi{i}}{\mathrm{3}}} =−\frac{\mathrm{1}}{\mathrm{2}}−{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow{e}^{{w}} =\frac{\mathrm{1}}{\:\sqrt{{e}}}{e}^{{i}\sqrt{\mathrm{3}}/\mathrm{2}} ,{e}^{{w}^{\mathrm{2}} } =\frac{\mathrm{1}}{\:\sqrt{{e}}}{e}^{−{i}\sqrt{\mathrm{3}}/\mathrm{2}} \\ $$$$\Rightarrow{e}^{{w}} +{e}^{{w}^{\mathrm{2}} } =\frac{\mathrm{2}}{\:\sqrt{{e}}}{cos}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{n}\right)!}=\frac{{e}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}\sqrt{{e}}}{cos}\left(\sqrt{\mathrm{3}}/\mathrm{2}\right) \\ $$

Commented by aleks041103 last updated on 21/Oct/22

Commented by Tawa11 last updated on 22/Oct/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Commented by infinityaction last updated on 22/Oct/22

thanks sir

$${thanks}\:{sir} \\ $$

Answered by ARUNG_Brandon_MBU last updated on 22/Oct/22

S=Σ_(n=0) ^∞ (1/((3n)!))=1+(1/(3!))+(1/(6!))+(1/(9!))+∙∙∙ =(1+(1/(1!))+(1/(2!))+(1/(3!))+(1/(4!))+(1/(5!))+(1/(6!))+(1/(7!))+(1/(8!))+(1/(9!))+∙∙∙)−((1/(1!))+(1/(2!))+(1/(4!))+(1/(5!))+(1/(7!))+(1/(8!))+∙∙∙) =e−((1/(1!))+(1/(4!))+(1/(7!))+∙∙∙)−((1/(2!))+(1/(5!))+(1/(8!))+∙∙∙)=e−Σ_(n=0) ^∞ (1/((3n+1)!))−Σ_(n=0) ^∞ (1/((3n+2)!)) ⇒e=Σ_(n=0) ^∞ (1/((3n)!))+Σ_(n=0) ^∞ (1/((3n+1)!))+Σ_(n=0) ^∞ (1/((3n+2)!)) e^x =Σ_(n=0) ^∞ (x^(3n) /((3n)!))+Σ_(n=0) ^∞ (x^(3n+1) /((3n+1)!))+Σ_(n=0) ^∞ (x^(3n+2) /((3n+2))) ⇒e^x =f(x)+f ′(x)+f ′′(x) Σ_(n=0) ^∞ (x^n /((3n)!)) is solution to this equation with f(0)=1 and f ′(0)=0 y_(gh) : r^2 +r+1=0 ⇒r=−(1/2)±i((√3)/2) ⇒y_(gh) =e^(−(x/( 2))) (αcos(((√3)/2)x)+βsin(((√3)/2)x)) y_p =ke^x =y_p ′=y_p ′′ ⇒e^x =ke^x +ke^x +ke^x ⇒k=(1/3) f(x)=y_(gh) +y_p =e^(−(x/2)) (αcos(((√3)/2)x)+βsin(((√3)/2)x))+(e^x /3) , f(0)=1 ⇒α+(1/3)=1 ⇒α=(2/3) f ′(x)=e^(−(x/2)) (((√3)/2)βcos(((√3)/2)x)−((√3)/2)αsin(((√3)/2)x))−(1/2)e^(−(x/2)) (αcos(((√3)/2)x)+βsin(((√3)/2)x))+(e^x /3) f ′(0)=0 ⇒((√3)/2)β−(α/2)+(1/3)=((√3)/2)β=0 ⇒β=0 ⇒f(x)=e^(−(x/2)) ((2/3)cos(((√3)/2)x))+(e^x /3) Σ_(n=0) ^∞ (1/((3n)!))=f(1)=(2/(3(√e)))cos(((√3)/2))+(e/3)=(1/3)(e+(2/( (√e)))cos(((√3)/2)))

$${S}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{n}\right)!}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{6}!}+\frac{\mathrm{1}}{\mathrm{9}!}+\centerdot\centerdot\centerdot \\ $$$$\:\:\:=\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}+\frac{\mathrm{1}}{\mathrm{5}!}+\frac{\mathrm{1}}{\mathrm{6}!}+\frac{\mathrm{1}}{\mathrm{7}!}+\frac{\mathrm{1}}{\mathrm{8}!}+\frac{\mathrm{1}}{\mathrm{9}!}+\centerdot\centerdot\centerdot\right)−\left(\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{4}!}+\frac{\mathrm{1}}{\mathrm{5}!}+\frac{\mathrm{1}}{\mathrm{7}!}+\frac{\mathrm{1}}{\mathrm{8}!}+\centerdot\centerdot\centerdot\right) \\ $$$$\:\:\:\:={e}−\left(\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{4}!}+\frac{\mathrm{1}}{\mathrm{7}!}+\centerdot\centerdot\centerdot\right)−\left(\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{5}!}+\frac{\mathrm{1}}{\mathrm{8}!}+\centerdot\centerdot\centerdot\right)={e}−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)!}−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{2}\right)!} \\ $$$$\Rightarrow{e}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{n}\right)!}+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)!}+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{2}\right)!} \\ $$$${e}^{{x}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{3}{n}} }{\left(\mathrm{3}{n}\right)!}+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{3}{n}+\mathrm{1}} }{\left(\mathrm{3}{n}+\mathrm{1}\right)!}+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{3}{n}+\mathrm{2}} }{\left(\mathrm{3}{n}+\mathrm{2}\right)}\:\Rightarrow{e}^{{x}} ={f}\left({x}\right)+{f}\:'\left({x}\right)+{f}\:''\left({x}\right) \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{\left(\mathrm{3}{n}\right)!}\:\mathrm{is}\:\mathrm{solution}\:\mathrm{to}\:\mathrm{this}\:\mathrm{equation}\:\mathrm{with}\:{f}\left(\mathrm{0}\right)=\mathrm{1}\:\mathrm{and}\:{f}\:'\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${y}_{{gh}} \::\:{r}^{\mathrm{2}} +{r}+\mathrm{1}=\mathrm{0}\:\Rightarrow{r}=−\frac{\mathrm{1}}{\mathrm{2}}\pm{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\Rightarrow{y}_{{gh}} ={e}^{−\frac{{x}}{\:\mathrm{2}}} \left(\alpha\mathrm{cos}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{x}\right)+\beta\mathrm{sin}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{x}\right)\right) \\ $$$${y}_{{p}} ={ke}^{{x}} ={y}_{{p}} '={y}_{{p}} ''\:\Rightarrow{e}^{{x}} ={ke}^{{x}} +{ke}^{{x}} +{ke}^{{x}} \:\Rightarrow{k}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${f}\left({x}\right)={y}_{{gh}} +{y}_{{p}} \:={e}^{−\frac{{x}}{\mathrm{2}}} \left(\alpha\mathrm{cos}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{x}\right)+\beta\mathrm{sin}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{x}\right)\right)+\frac{{e}^{{x}} }{\mathrm{3}}\:\:,\:{f}\left(\mathrm{0}\right)=\mathrm{1}\:\Rightarrow\alpha+\frac{\mathrm{1}}{\mathrm{3}}=\mathrm{1}\:\Rightarrow\alpha=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${f}\:'\left({x}\right)={e}^{−\frac{{x}}{\mathrm{2}}} \left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\beta\mathrm{cos}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{x}\right)−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\alpha\mathrm{sin}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{x}\right)\right)−\frac{\mathrm{1}}{\mathrm{2}}{e}^{−\frac{{x}}{\mathrm{2}}} \left(\alpha\mathrm{cos}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{x}\right)+\beta\mathrm{sin}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{x}\right)\right)+\frac{{e}^{{x}} }{\mathrm{3}} \\ $$$${f}\:'\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\beta−\frac{\alpha}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\beta=\mathrm{0}\:\Rightarrow\beta=\mathrm{0}\:\Rightarrow{f}\left({x}\right)={e}^{−\frac{{x}}{\mathrm{2}}} \left(\frac{\mathrm{2}}{\mathrm{3}}\mathrm{cos}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{x}\right)\right)+\frac{{e}^{{x}} }{\mathrm{3}} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{n}\right)!}={f}\left(\mathrm{1}\right)=\frac{\mathrm{2}}{\mathrm{3}\sqrt{{e}}}\mathrm{cos}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)+\frac{{e}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}}\left({e}+\frac{\mathrm{2}}{\:\sqrt{{e}}}\mathrm{cos}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\right) \\ $$

Commented by infinityaction last updated on 22/Oct/22

thanks

$${thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com