
Question and Answers Forum
Question Number 18003 by Tinkutara last updated on 13/Jul/17
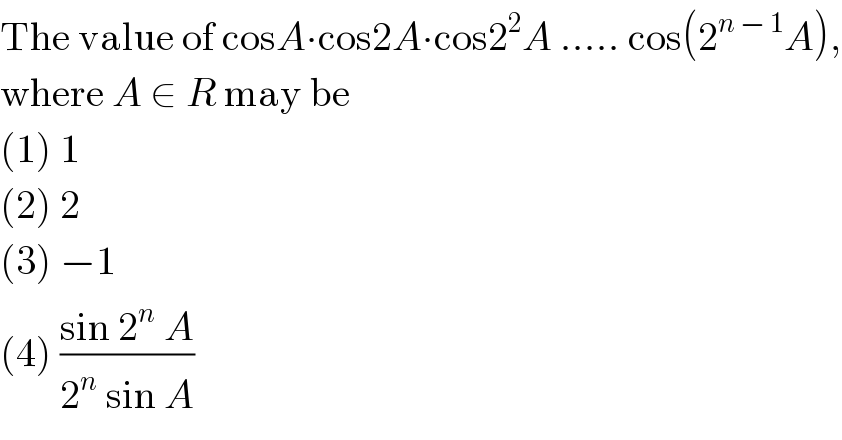
Answered by alex041103 last updated on 13/Jul/17
![Let E=cos(A)cos(2A)...=Π_(k=0) ^(n−1) cos(2^k A) Because sin(2^(k+1) A)=2sin(2^k A)cos(2^k A) ⇒cos(2^k A)=((sin(2^(k+1) A))/(2sin(2^k A))) ⇒E=Π_(k=0) ^(n−1) ((sin(2^(k+1) A))/(2sin(2^k A)))= =[Π_(k=0) ^(n−1) sin(2^(k+1) A)]×[Π_(k=0) ^(n−1) (1/(2sin(2^k A)))] =((sin(2^n A))/(2sin(A)))[Π_(k=0) ^(n−2) sin(2^(k+1) A)][Π_(k=1) ^(n−1) (1/(2sin(2^k A)))] =((sin(2^n A))/(2sin(A)))[Π_(k=1) ^(n−1) sin(2^k A)][Π_(k=1) ^(n−1) (1/(2sin(2^k A)))] =((sin(2^n A))/(2sin(A)))[Π_(k=1) ^(n−1) ((sin(2^k A))/(2sin(2^k A)))] =((sin(2^n A))/(2sin(A)))[Π_(k=1) ^(n−1) (1/2)] =((sin(2^n A))/(2sin(A)))×(1/2^(n−1) ) =((sun(2^n A))/(2^n sin(A))) = cos(A)cos(2A)...](Q18010.png)
Commented by Tinkutara last updated on 13/Jul/17

Commented by alex041103 last updated on 13/Jul/17
Commented by Tinkutara last updated on 13/Jul/17

