
Question and Answers Forum
Question Number 18015 by alex041103 last updated on 13/Jul/17
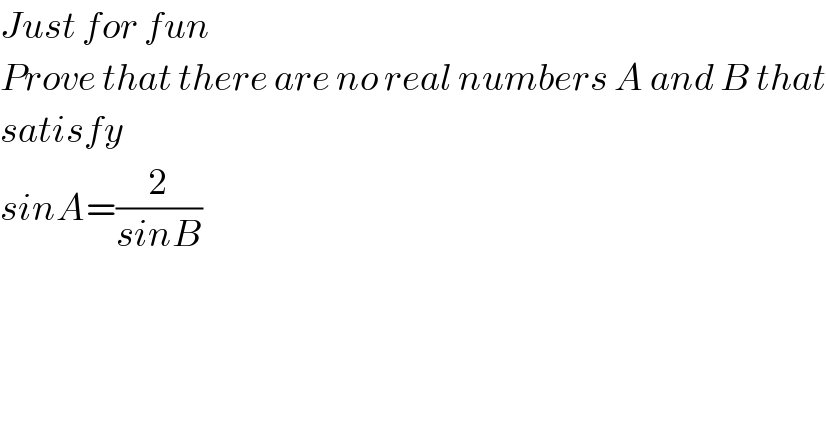
Commented by alex041103 last updated on 13/Jul/17
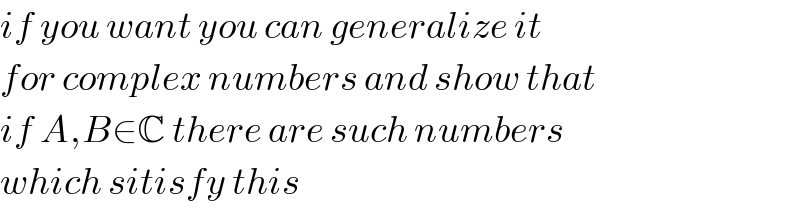
Answered by Tinkutara last updated on 13/Jul/17
![LHS ∈ [−1, 1] but RHS ∈ (−∞, −2] ∪ [2, ∞) hence there is no solution in real numbers.](Q18017.png)
Commented by alex041103 last updated on 14/Jul/17
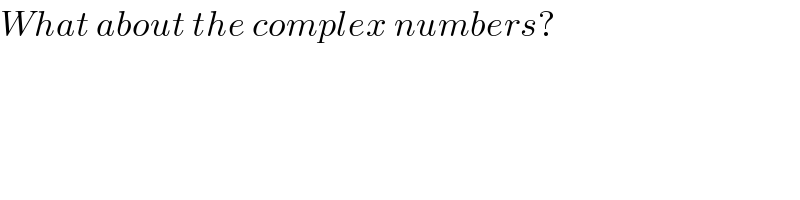
Commented by alex041103 last updated on 14/Jul/17

Commented by alex041103 last updated on 14/Jul/17
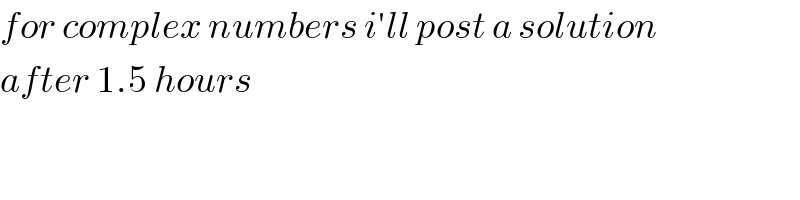
Answered by alex041103 last updated on 14/Jul/17
![Tinkutara did a nice proof for the case where A,B∈R But what about the case where A,B∈C (complex numbers) We know that for z∈C, sin z ∈(−∞,∞) So clearly there are solutions. In fact there are infinate number of solutions. We know that for z∈C (1) e^(iz) =cos z + isin z (Euler′s formula) ⇒e^(i(−z)) =cos z−isin z or (2) −e^(−iz) =−cos z + isin z Then we add (1) and (2) 2isin z = e^(iz) − e^(−iz) ⇒sin z = ((e^(iz) − e^(−iz) )/(2i)) Now let′s define sin^(−1) (z) using the complex definition for sin z. Let s = sin z ⇒2is=e^(iz) −e^(−iz) 2ise^(iz) =(e^(iz) )^2 −1 let t=e^(iz) t^2 −2ist−1=0 ⇒t_(1;2) =((2is±(√(−4s^2 +4)))/2)=is±(√(1−s^2 )) ⇒ln(e^(iz) )=ln(is±(√(1−s^2 )))=iz ⇒z=sin^(−1) (s)=−i ln(is±(√(1−s^2 ))) And you can see if you substitute back s=sin z, after you simplify you′ll get sin^(−1) (sin z)=z. So now sinA=(2/(sinB)) ⇒A=sin^(−1) ((2/(sin B))) we insert that into the formula and we get A=−i ln(((2i)/(sin B))±(√(1−(4/(sin^2 B))))) And we add 2kπ (k∈Z) because sin(A)=sin(A+2π) A=−i ln(((2i)/(sin B))±(√(1−(4/(sin^2 B))))) +2kπ Example: sin A=(2/(sin 45°))=2(√2) A=−i ln(((2i)/((((√2)/2))))±(√(1−(4/(((2/4))))))) + 2kπ= =−i ln(2(√2)i±(√(−7)))+2kπ= =−i ln(2(√2)i±i(√7))+2kπ= =−i ln[i((√8)±(√7))]+2kπ= =−i[ln(i)+ln((√8)±(√7))]+2kπ We now that z=a+bi=r(cosθ + isinθ)=re^(iθ) ⇒z=e^(ln(r) + iθ) ⇒ln(z)=ln(r) + iθ where r=(√(a^2 +b^2 )) and θ=tan^(−1) ((b/a)). In our case ln(i)=ln(1)+i(π/2)=((πi)/2) ⇒A=−i×((πi)/2) − iln((√8)±(√7))+2kπ =(π/2)−iln((√8)±(√7)) + 2kπ ⇒A=(π/2)−i ln((√8)±(√7))+2kπ, k∈Z](Q18060.png)
