
Question Number 180641 by mr W last updated on 14/Nov/22
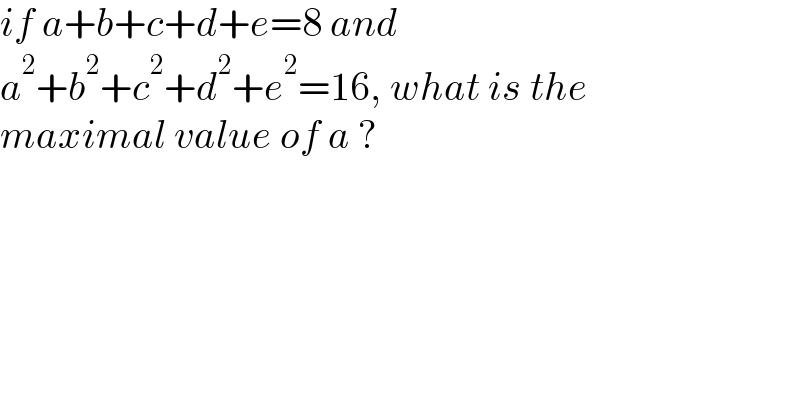
$${if}\:{a}+{b}+{c}+{d}+{e}=\mathrm{8}\:{and} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} +{e}^{\mathrm{2}} =\mathrm{16},\:{what}\:{is}\:{the} \\ $$$${maximal}\:{value}\:{of}\:{a}\:? \\ $$
Answered by Emrice last updated on 14/Nov/22

$${a}<\mathrm{4} \\ $$
Commented by Rasheed.Sindhi last updated on 15/Nov/22

$${a}\leqslant\mathrm{4} \\ $$
Commented by mr W last updated on 15/Nov/22

$${if}\:{a}=\mathrm{4},\:{then}\:{b}={c}={d}={e}=\mathrm{0},\:{and} \\ $$$${a}+{b}+{c}+{d}+{e}=\mathrm{4}\neq\mathrm{8},\:{therefore}\:{a}\:{must} \\ $$$${be}\:{less}\:{than}\:\mathrm{4}. \\ $$
Commented by Rasheed.Sindhi last updated on 15/Nov/22

$${Yes}\:{sir}\:{I}\:{understood}. \\ $$
Answered by a.lgnaoui last updated on 15/Nov/22

$$\mathrm{4} \\ $$
Answered by manxsol last updated on 15/Nov/22
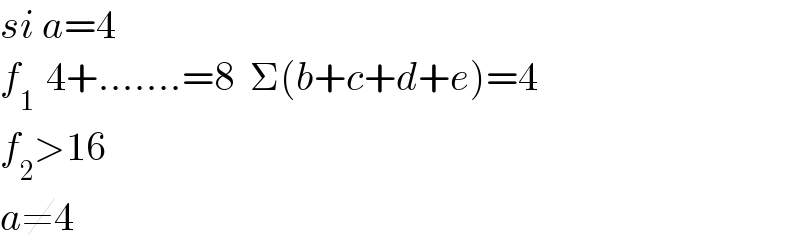
$${si}\:{a}=\mathrm{4} \\ $$$${f}_{\mathrm{1}\:\:\:} \mathrm{4}+.......=\mathrm{8}\:\:\Sigma\left({b}+{c}+{d}+{e}\right)=\mathrm{4} \\ $$$${f}_{\mathrm{2}} >\mathrm{16} \\ $$$${a}\neq\mathrm{4} \\ $$
Commented by manxsol last updated on 15/Nov/22

$${si}\:{a}=\mathrm{4} \\ $$$${f}_{\mathrm{1}\:\:\:} \mathrm{4}+.......=\mathrm{8}\:\:\Sigma\left({b}+{c}+{d}+{e}\right)=\mathrm{4} \\ $$$${f}_{\mathrm{2}} >\mathrm{16} \\ $$$${a}\neq\mathrm{4} \\ $$$$\begin{array}{|c|c|c|}{{a}}&\hline{{b}}&\hline{{c}}&\hline{{d}}&\hline{{e}}&\hline{}\\{\mathrm{3}}&\hline{\mathrm{2}}&\hline{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\mathrm{8}}\\{\mathrm{9}}&\hline{\mathrm{4}}&\hline{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\mathrm{16}}\\\hline\end{array} \\ $$
Commented by mr W last updated on 15/Nov/22
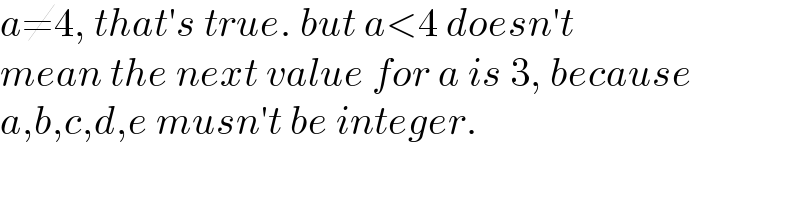
$${a}\neq\mathrm{4},\:{that}'{s}\:{true}.\:{but}\:{a}<\mathrm{4}\:{doesn}'{t} \\ $$$${mean}\:{the}\:{next}\:{value}\:{for}\:{a}\:{is}\:\mathrm{3},\:{because} \\ $$$${a},{b},{c},{d},{e}\:{musn}'{t}\:{be}\:{integer}. \\ $$
Answered by mr W last updated on 15/Nov/22
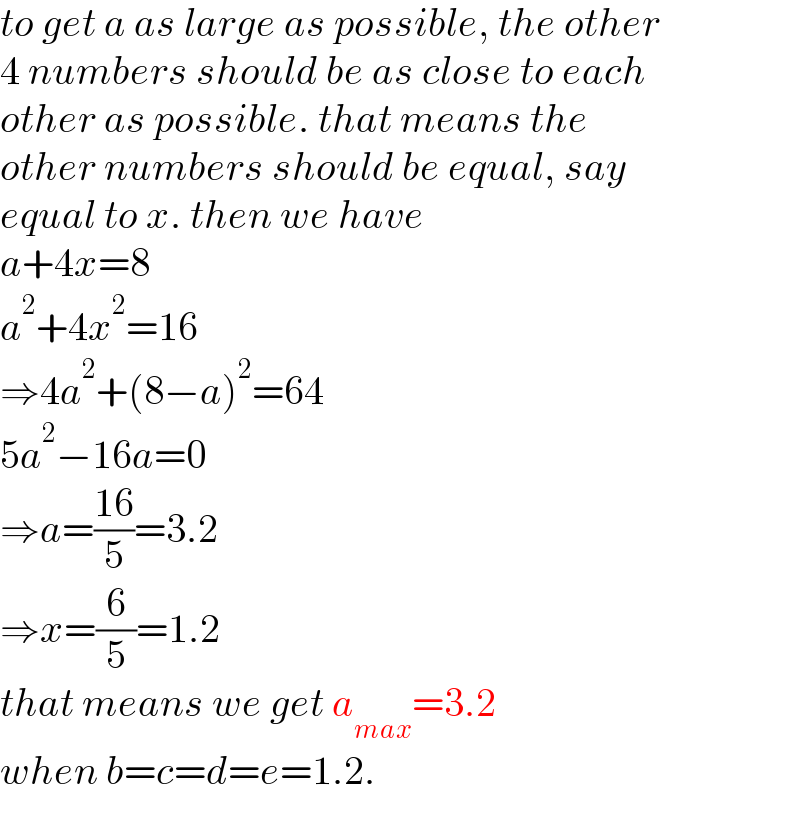
$${to}\:{get}\:{a}\:{as}\:{large}\:{as}\:{possible},\:{the}\:{other} \\ $$$$\mathrm{4}\:{numbers}\:{should}\:{be}\:{as}\:{close}\:{to}\:{each} \\ $$$${other}\:{as}\:{possible}.\:{that}\:{means}\:{the}\: \\ $$$${other}\:{numbers}\:{should}\:{be}\:{equal},\:{say}\: \\ $$$${equal}\:{to}\:{x}.\:{then}\:{we}\:{have} \\ $$$${a}+\mathrm{4}{x}=\mathrm{8} \\ $$$${a}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{2}} =\mathrm{16} \\ $$$$\Rightarrow\mathrm{4}{a}^{\mathrm{2}} +\left(\mathrm{8}−{a}\right)^{\mathrm{2}} =\mathrm{64} \\ $$$$\mathrm{5}{a}^{\mathrm{2}} −\mathrm{16}{a}=\mathrm{0} \\ $$$$\Rightarrow{a}=\frac{\mathrm{16}}{\mathrm{5}}=\mathrm{3}.\mathrm{2} \\ $$$$\Rightarrow{x}=\frac{\mathrm{6}}{\mathrm{5}}=\mathrm{1}.\mathrm{2} \\ $$$${that}\:{means}\:{we}\:{get}\:{a}_{{max}} =\mathrm{3}.\mathrm{2} \\ $$$${when}\:{b}={c}={d}={e}=\mathrm{1}.\mathrm{2}. \\ $$
Commented by manxsol last updated on 15/Nov/22
Thanks Mr.W. I am learn.
Commented by mr W last updated on 15/Nov/22
![an other method (little thinking, just applying formula) a=8−(b+c+d+e) (8−b−c−d−e)^2 +b^2 +c^2 +d^2 +e^2 −16=0 Φ=8−(b+c+d+e)+λ[(8−b−c−d−e)^2 +b^2 +c^2 +d^2 +e^2 −16] (∂Φ/∂b)=−1+λ[−2(8−b−c−d−e)+2b]=0 ⇒b=(1/(2λ))+8−(b+c+d+e) similarly ⇒c=(1/(2λ))+8−(b+c+d+e) ⇒d=(1/(2λ))+8−(b+c+d+e) ⇒e=(1/(2λ))+8−(b+c+d+e) ⇒b=c=d=e=x, say (∂Φ/∂λ)=(8−b−c−d−e)^2 +b^2 +c^2 +d^2 +e^2 −16=0 ⇒(8−4x)^2 +4x^2 −16=0 5x^2 −16x+12=0 ⇒x=((8±2)/5)=2 or (6/5) ⇒a=0 (min) or ((16)/5) (max)](Q180697.png)
$${an}\:{other}\:{method} \\ $$$$\left({little}\:{thinking},\:{just}\:{applying}\:{formula}\right) \\ $$$${a}=\mathrm{8}−\left({b}+{c}+{d}+{e}\right) \\ $$$$\left(\mathrm{8}−{b}−{c}−{d}−{e}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} +{e}^{\mathrm{2}} −\mathrm{16}=\mathrm{0} \\ $$$$\Phi=\mathrm{8}−\left({b}+{c}+{d}+{e}\right)+\lambda\left[\left(\mathrm{8}−{b}−{c}−{d}−{e}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} +{e}^{\mathrm{2}} −\mathrm{16}\right] \\ $$$$\frac{\partial\Phi}{\partial{b}}=−\mathrm{1}+\lambda\left[−\mathrm{2}\left(\mathrm{8}−{b}−{c}−{d}−{e}\right)+\mathrm{2}{b}\right]=\mathrm{0} \\ $$$$\Rightarrow{b}=\frac{\mathrm{1}}{\mathrm{2}\lambda}+\mathrm{8}−\left({b}+{c}+{d}+{e}\right) \\ $$$${similarly} \\ $$$$\Rightarrow{c}=\frac{\mathrm{1}}{\mathrm{2}\lambda}+\mathrm{8}−\left({b}+{c}+{d}+{e}\right) \\ $$$$\Rightarrow{d}=\frac{\mathrm{1}}{\mathrm{2}\lambda}+\mathrm{8}−\left({b}+{c}+{d}+{e}\right) \\ $$$$\Rightarrow{e}=\frac{\mathrm{1}}{\mathrm{2}\lambda}+\mathrm{8}−\left({b}+{c}+{d}+{e}\right) \\ $$$$\Rightarrow{b}={c}={d}={e}={x},\:{say} \\ $$$$\frac{\partial\Phi}{\partial\lambda}=\left(\mathrm{8}−{b}−{c}−{d}−{e}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} +{e}^{\mathrm{2}} −\mathrm{16}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{8}−\mathrm{4}{x}\right)^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}=\mathrm{0} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} −\mathrm{16}{x}+\mathrm{12}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{8}\pm\mathrm{2}}{\mathrm{5}}=\mathrm{2}\:{or}\:\frac{\mathrm{6}}{\mathrm{5}} \\ $$$$\Rightarrow{a}=\mathrm{0}\:\left({min}\right)\:{or}\:\frac{\mathrm{16}}{\mathrm{5}}\:\left({max}\right) \\ $$
Commented by mr W last updated on 16/Nov/22

$${Using}\:{Lagrange}\:{Multiplier}\:{method} \\ $$$${for}\:{finding}\:{local}\:{maximum}\:{or}\: \\ $$$${minimum}\:{of}\:{a}\:{function}\:{with}\:{more} \\ $$$${than}\:{one}\:{variable}\:{under}\:{a}\:{constraint}. \\ $$
Commented by manolex last updated on 16/Nov/22
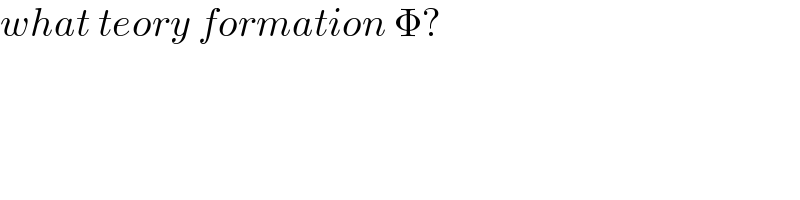
$${what}\:{teory}\:{formation}\:\Phi? \\ $$
Commented by mr W last updated on 16/Nov/22
https://www.wikihow.com/Use-Lagrange-Multipliers
