Question Number 180680 by cortano1 last updated on 15/Nov/22
Answered by ARUNG_Brandon_MBU last updated on 16/Nov/22
![I=∫_0 ^1 ((x−1+(√(x^2 +1)))/(x+1+(√(x^2 +1))))dx, x=sinhθ =∫_0 ^(ln(1+(√2))) ((sinhθ−1+coshθ)/(sinhθ+1+coshθ))(coshθdθ) =∫_0 ^(ln(1+(√2))) ((e^θ −1)/(e^θ +1))∙((e^(2θ) +1)/(2e^θ ))dθ=(1/2)∫_1 ^(1+(√2)) (((t−1)(t^2 +1))/(t^2 +t))((dt/t)) =(1/2)∫_1 ^(1+(√2)) ((t^3 −t^2 +t−1)/(t^3 +t^2 ))dt=(1/2)∫_1 ^(1+(√2)) (1−((2t^2 −t+1)/(t^3 +t^2 )))dt =((√2)/2)−(1/2)∫_1 ^(1+(√2)) ((2t^2 −t+1)/(t^2 (t+1)))dt=((√2)/2)−(1/2)∫_1 ^(1+(√2)) ((4/(t+1))−((2t−1)/t^2 ))dt =((√2)/2)−(1/2)[4ln(t+1)−2ln(t)−(1/t)]_1 ^(1+(√2)) =((√2)/2)−2ln(((2+(√2))/2))+ln(1+(√2))+((1/2)/(1+(√2)))−(1/2) =(((√2)−1)/2)−2ln(2+(√2))+ln4+ln(1+(√2))+(((√2)−1)/2) =(√2)−1+ln4−2ln(2+(√2))+ln(1+(√2))](Q180704.png)
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}−\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}+\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{dx},\:{x}=\mathrm{sinh}\theta \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \frac{\mathrm{sinh}\theta−\mathrm{1}+\mathrm{cosh}\theta}{\mathrm{sinh}\theta+\mathrm{1}+\mathrm{cosh}\theta}\left(\mathrm{cosh}\theta{d}\theta\right) \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \frac{{e}^{\theta} −\mathrm{1}}{{e}^{\theta} +\mathrm{1}}\centerdot\frac{{e}^{\mathrm{2}\theta} +\mathrm{1}}{\mathrm{2}{e}^{\theta} }{d}\theta=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \frac{\left({t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{{t}^{\mathrm{2}} +{t}}\left(\frac{{dt}}{{t}}\right) \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \frac{{t}^{\mathrm{3}} −{t}^{\mathrm{2}} +{t}−\mathrm{1}}{{t}^{\mathrm{3}} +{t}^{\mathrm{2}} }{dt}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \left(\mathrm{1}−\frac{\mathrm{2}{t}^{\mathrm{2}} −{t}+\mathrm{1}}{{t}^{\mathrm{3}} +{t}^{\mathrm{2}} }\right){dt} \\ $$$$\:\:\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \frac{\mathrm{2}{t}^{\mathrm{2}} −{t}+\mathrm{1}}{{t}^{\mathrm{2}} \left({t}+\mathrm{1}\right)}{dt}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \left(\frac{\mathrm{4}}{{t}+\mathrm{1}}−\frac{\mathrm{2}{t}−\mathrm{1}}{{t}^{\mathrm{2}} }\right){dt} \\ $$$$\:\:\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{4ln}\left({t}+\mathrm{1}\right)−\mathrm{2ln}\left({t}\right)−\frac{\mathrm{1}}{{t}}\right]_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \\ $$$$\:\:\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\mathrm{2ln}\left(\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{2}}\right)+\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)+\frac{\mathrm{1}/\mathrm{2}}{\mathrm{1}+\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:=\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{2}}−\mathrm{2ln}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)+\mathrm{ln4}+\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)+\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:=\sqrt{\mathrm{2}}−\mathrm{1}+\mathrm{ln4}−\mathrm{2ln}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)+\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$
Commented by MJS_new last updated on 16/Nov/22
$$\mathrm{ln}\:\mathrm{4}\:−\mathrm{2ln}\:\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\:+\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\:= \\ $$$$=\mathrm{ln}\:\left(\frac{\mathrm{4}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}{\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }\right)\:=−\mathrm{ln}\:\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{our}\:\mathrm{answers}\:\mathrm{are}\:\mathrm{equal} \\ $$
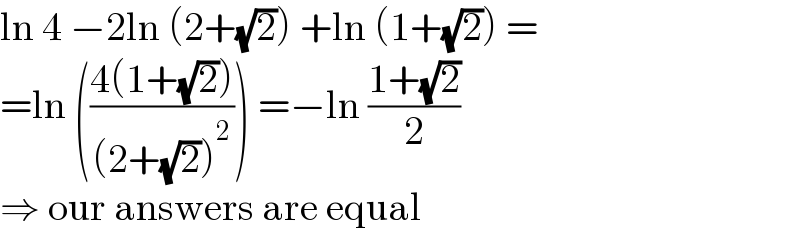
Commented by cortano1 last updated on 16/Nov/22
$$\mathrm{yes}..\mathrm{thx} \\ $$
Answered by MJS_new last updated on 16/Nov/22
![without substitution: ∫((x−1+(√(x^2 +1)))/(x+1+(√(x^2 +1))))dx= =∫((−1+(√(x^2 +1)))/x)dx= =∫(((1+(√(x^2 +1)))/x)−(2/x))dx= =∫((x/(−1+(√(x^2 +1))))−(2/x))dx= =∫((x/(−1+(√(x^2 +1))))−(x/( (√(x^2 +1))))+(x/( (√(x^2 +1))))−(2/x))dx= =∫((x/( (√(x^2 +1))))×(1/(−1+(√(x^2 +1))))+(x/( (√(x^2 +1))))−(2/x))dx= =∫((d[−1+(√(x^2 +1))])/(−1+(√(x^2 +1))))+∫d[(√(x^2 +1))]−2∫(dx/x)= =ln (−1+(√(x^2 +1))) +(√(x^2 +1))−2ln x +C ⇒ answer is −1+(√2)−ln ((1+(√2))/2)](Q180706.png)
$$\mathrm{without}\:\mathrm{substitution}: \\ $$$$\int\frac{{x}−\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}+\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{dx}= \\ $$$$=\int\frac{−\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}}{dx}= \\ $$$$=\int\left(\frac{\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}}−\frac{\mathrm{2}}{{x}}\right){dx}= \\ $$$$=\int\left(\frac{{x}}{−\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}−\frac{\mathrm{2}}{{x}}\right){dx}= \\ $$$$=\int\left(\frac{{x}}{−\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}−\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}+\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}−\frac{\mathrm{2}}{{x}}\right){dx}= \\ $$$$=\int\left(\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}×\frac{\mathrm{1}}{−\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}+\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}−\frac{\mathrm{2}}{{x}}\right){dx}= \\ $$$$=\int\frac{{d}\left[−\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right]}{−\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}+\int{d}\left[\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right]−\mathrm{2}\int\frac{{dx}}{{x}}= \\ $$$$=\mathrm{ln}\:\left(−\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)\:+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−\mathrm{2ln}\:{x}\:+{C} \\ $$$$\Rightarrow \\ $$$$\mathrm{answer}\:\mathrm{is}\:−\mathrm{1}+\sqrt{\mathrm{2}}−\mathrm{ln}\:\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$
Commented by cortano1 last updated on 16/Nov/22
$$\mathrm{yes}\:\mathrm{thx} \\ $$
Answered by MJS_new last updated on 16/Nov/22
![∫((x−1+(√(x^2 +1)))/(x+1+(√(x^2 +1))))dx= [t=x+(√(x^2 +1)) → dx=((t^2 +1)/(2t^2 ))dt] =(1/2)∫(((t−1)(t^2 +1))/(t^2 (t+1)))dt= =∫((1/2)+(1/t)−(2/(t+1))−(1/(2t^2 )))dt= =(1/2)t+ln t −2ln (t+1) +(1/(2t))= =((t^2 +1)/(2t))+ln (t/((t+1)^2 )) = =(√(x^2 +1))+ln ((−1+(√(x^2 +1)))/x^2 )+C](Q180707.png)
$$\int\frac{{x}−\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}+\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\rightarrow\:{dx}=\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} }{dt}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left({t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{{t}^{\mathrm{2}} \left({t}+\mathrm{1}\right)}{dt}= \\ $$$$=\int\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{{t}}−\frac{\mathrm{2}}{{t}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} }\right){dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{t}+\mathrm{ln}\:{t}\:−\mathrm{2ln}\:\left({t}+\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{2}{t}}= \\ $$$$=\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{t}}+\mathrm{ln}\:\frac{{t}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\:= \\ $$$$=\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}+\mathrm{ln}\:\frac{−\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}^{\mathrm{2}} }+{C} \\ $$
Answered by Gamil last updated on 16/Nov/22
