Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 180728 by CrispyXYZ last updated on 16/Nov/22

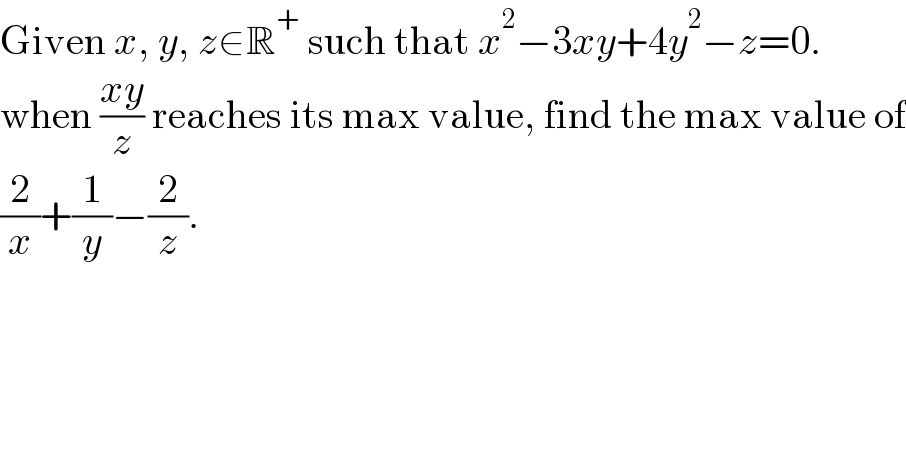
Given x, y, z∈R^+ such that x^2 −3xy+4y^2 −z=0. when ((xy)/z) reaches its max value, find the max value of (2/x)+(1/y)−(2/z).

$$\mathrm{Given}\:{x},\:{y},\:{z}\in\mathbb{R}^{+} \:\mathrm{such}\:\mathrm{that}\:{x}^{\mathrm{2}} −\mathrm{3}{xy}+\mathrm{4}{y}^{\mathrm{2}} −{z}=\mathrm{0}. \\ $$$$\mathrm{when}\:\frac{{xy}}{{z}}\:\mathrm{reaches}\:\mathrm{its}\:\mathrm{max}\:\mathrm{value},\:\mathrm{find}\:\mathrm{the}\:\mathrm{max}\:\mathrm{value}\:\mathrm{of} \\ $$$$\frac{\mathrm{2}}{{x}}+\frac{\mathrm{1}}{{y}}−\frac{\mathrm{2}}{{z}}. \\ $$

Answered by mr W last updated on 20/Nov/22

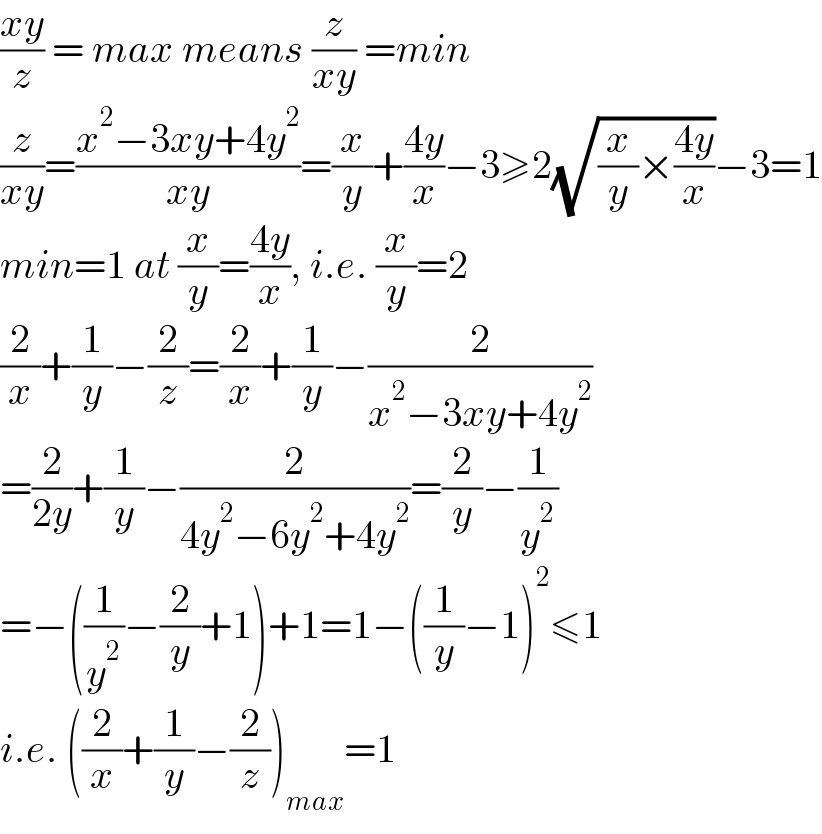
((xy)/z) = max means (z/(xy)) =min (z/(xy))=((x^2 −3xy+4y^2 )/(xy))=(x/y)+((4y)/x)−3≥2(√((x/y)×((4y)/x)))−3=1 min=1 at (x/y)=((4y)/x), i.e. (x/y)=2 (2/x)+(1/y)−(2/z)=(2/x)+(1/y)−(2/(x^2 −3xy+4y^2 )) =(2/(2y))+(1/y)−(2/(4y^2 −6y^2 +4y^2 ))=(2/y)−(1/y^2 ) =−((1/y^2 )−(2/y)+1)+1=1−((1/y)−1)^2 ≤1 i.e. ((2/x)+(1/y)−(2/z))_(max) =1

$$\frac{{xy}}{{z}}\:=\:{max}\:{means}\:\frac{{z}}{{xy}}\:={min} \\ $$$$\frac{{z}}{{xy}}=\frac{{x}^{\mathrm{2}} −\mathrm{3}{xy}+\mathrm{4}{y}^{\mathrm{2}} }{{xy}}=\frac{{x}}{{y}}+\frac{\mathrm{4}{y}}{{x}}−\mathrm{3}\geqslant\mathrm{2}\sqrt{\frac{{x}}{{y}}×\frac{\mathrm{4}{y}}{{x}}}−\mathrm{3}=\mathrm{1} \\ $$$${min}=\mathrm{1}\:{at}\:\frac{{x}}{{y}}=\frac{\mathrm{4}{y}}{{x}},\:{i}.{e}.\:\frac{{x}}{{y}}=\mathrm{2} \\ $$$$\frac{\mathrm{2}}{{x}}+\frac{\mathrm{1}}{{y}}−\frac{\mathrm{2}}{{z}}=\frac{\mathrm{2}}{{x}}+\frac{\mathrm{1}}{{y}}−\frac{\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{3}{xy}+\mathrm{4}{y}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}}{\mathrm{2}{y}}+\frac{\mathrm{1}}{{y}}−\frac{\mathrm{2}}{\mathrm{4}{y}^{\mathrm{2}} −\mathrm{6}{y}^{\mathrm{2}} +\mathrm{4}{y}^{\mathrm{2}} }=\frac{\mathrm{2}}{{y}}−\frac{\mathrm{1}}{{y}^{\mathrm{2}} } \\ $$$$=−\left(\frac{\mathrm{1}}{{y}^{\mathrm{2}} }−\frac{\mathrm{2}}{{y}}+\mathrm{1}\right)+\mathrm{1}=\mathrm{1}−\left(\frac{\mathrm{1}}{{y}}−\mathrm{1}\right)^{\mathrm{2}} \leqslant\mathrm{1} \\ $$$${i}.{e}.\:\left(\frac{\mathrm{2}}{{x}}+\frac{\mathrm{1}}{{y}}−\frac{\mathrm{2}}{{z}}\right)_{{max}} =\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com