
Question and Answers Forum
Question Number 180839 by Mastermind last updated on 17/Nov/22
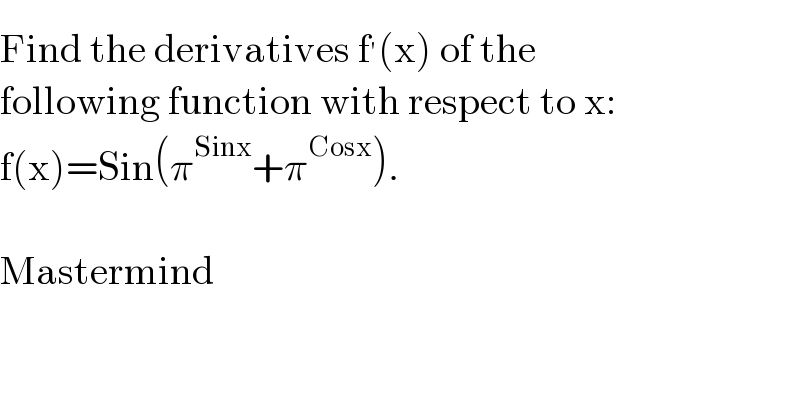
Answered by saboorhalimi last updated on 17/Nov/22
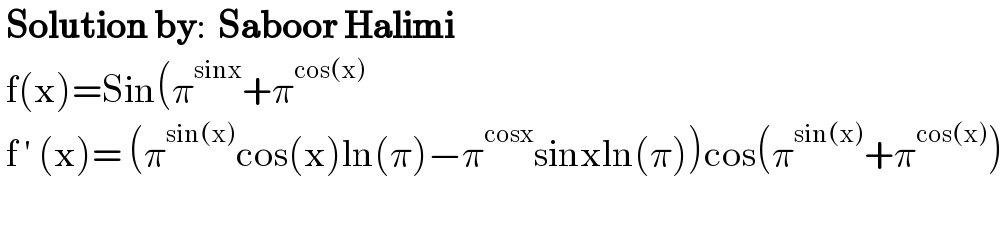
Commented by Mastermind last updated on 17/Nov/22
Commented by Acem last updated on 17/Nov/22
![(e^x )′ = x′ e^x ln e= 1×e^x ×1= e^x (a^u )′= ln a× u′×a^u here a= π (cos u)′ = −u′ sin u (sin u)′ = u^′ cos u [sin (π^(sin x) + π^(cos x) )]^′ = (π^(sin x) + π^(cos x) )′ .cos (π^(sin x) + π^(cos x) ) (π^(sin x) + π^(cos x) )′ = (π^(sin x) )^′ + (π^(cos x) )′ (a^u )′ look above = ln π.cos x π^( sin x) − ln π . sin x . π^( cos x) f(x)′= ln π(cos x π^( sin x) − sin x . π^( cos x) )cos (π^(sin x) + π^(cos x) )](Q180848.png)
| ||
Question and Answers Forum | ||
Question Number 180839 by Mastermind last updated on 17/Nov/22 | ||
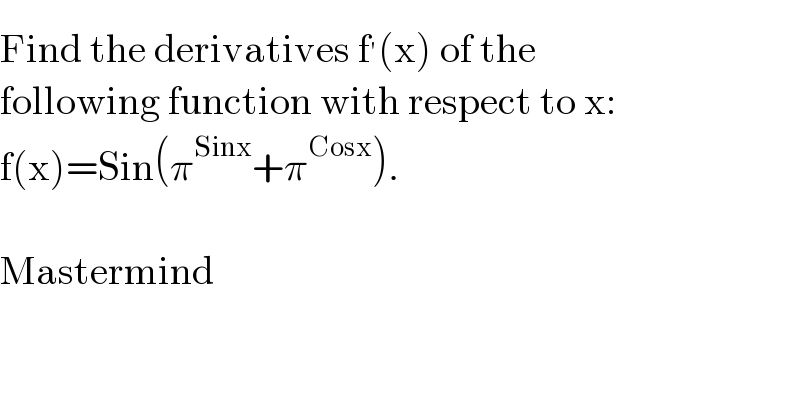 | ||
Answered by saboorhalimi last updated on 17/Nov/22 | ||
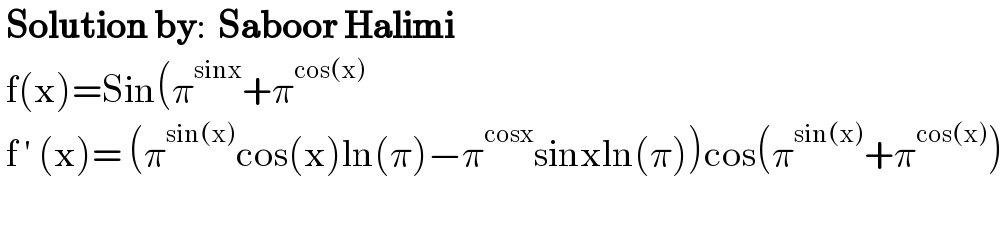 | ||
| ||
Commented by Mastermind last updated on 17/Nov/22 | ||
 | ||
Commented by Acem last updated on 17/Nov/22 | ||
![(e^x )′ = x′ e^x ln e= 1×e^x ×1= e^x (a^u )′= ln a× u′×a^u here a= π (cos u)′ = −u′ sin u (sin u)′ = u^′ cos u [sin (π^(sin x) + π^(cos x) )]^′ = (π^(sin x) + π^(cos x) )′ .cos (π^(sin x) + π^(cos x) ) (π^(sin x) + π^(cos x) )′ = (π^(sin x) )^′ + (π^(cos x) )′ (a^u )′ look above = ln π.cos x π^( sin x) − ln π . sin x . π^( cos x) f(x)′= ln π(cos x π^( sin x) − sin x . π^( cos x) )cos (π^(sin x) + π^(cos x) )](Q180848.png) | ||