
Question and Answers Forum
Question Number 180882 by mr W last updated on 18/Nov/22

Commented by mr W last updated on 18/Nov/22
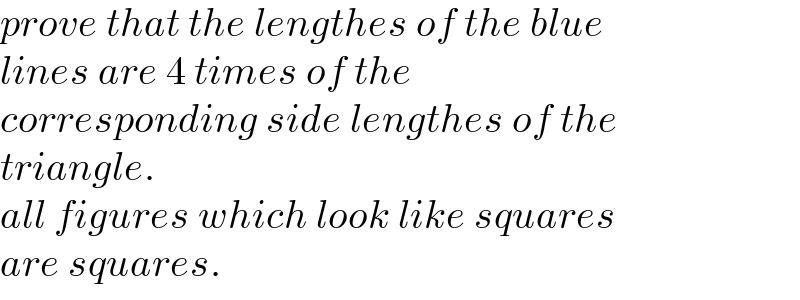
Answered by mr W last updated on 19/Nov/22

Commented by mr W last updated on 19/Nov/22
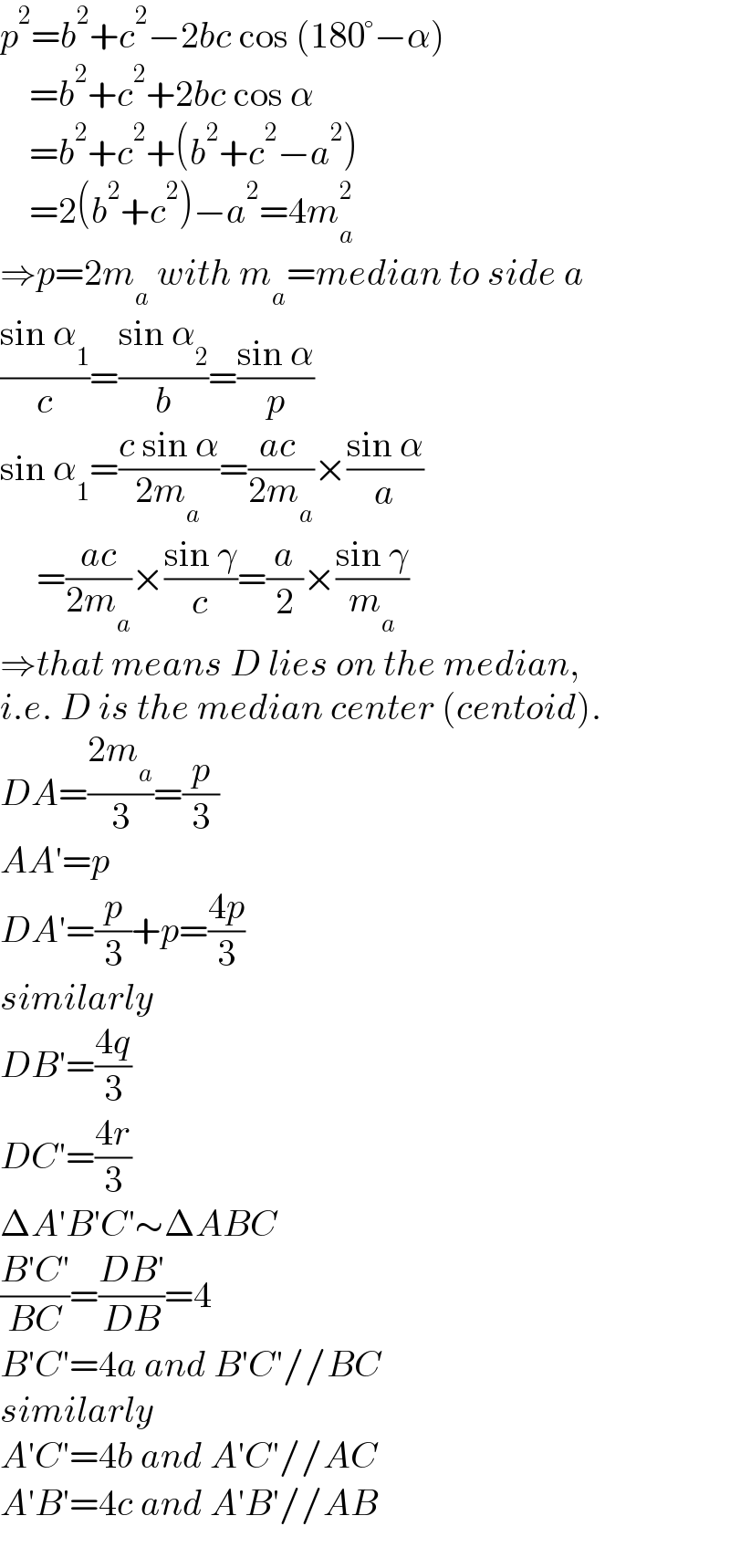
| ||
Question and Answers Forum | ||
Question Number 180882 by mr W last updated on 18/Nov/22 | ||
 | ||
Commented by mr W last updated on 18/Nov/22 | ||
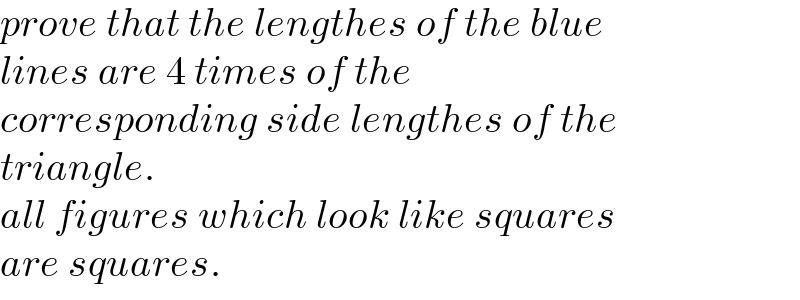 | ||
Answered by mr W last updated on 19/Nov/22 | ||
 | ||
Commented by mr W last updated on 19/Nov/22 | ||
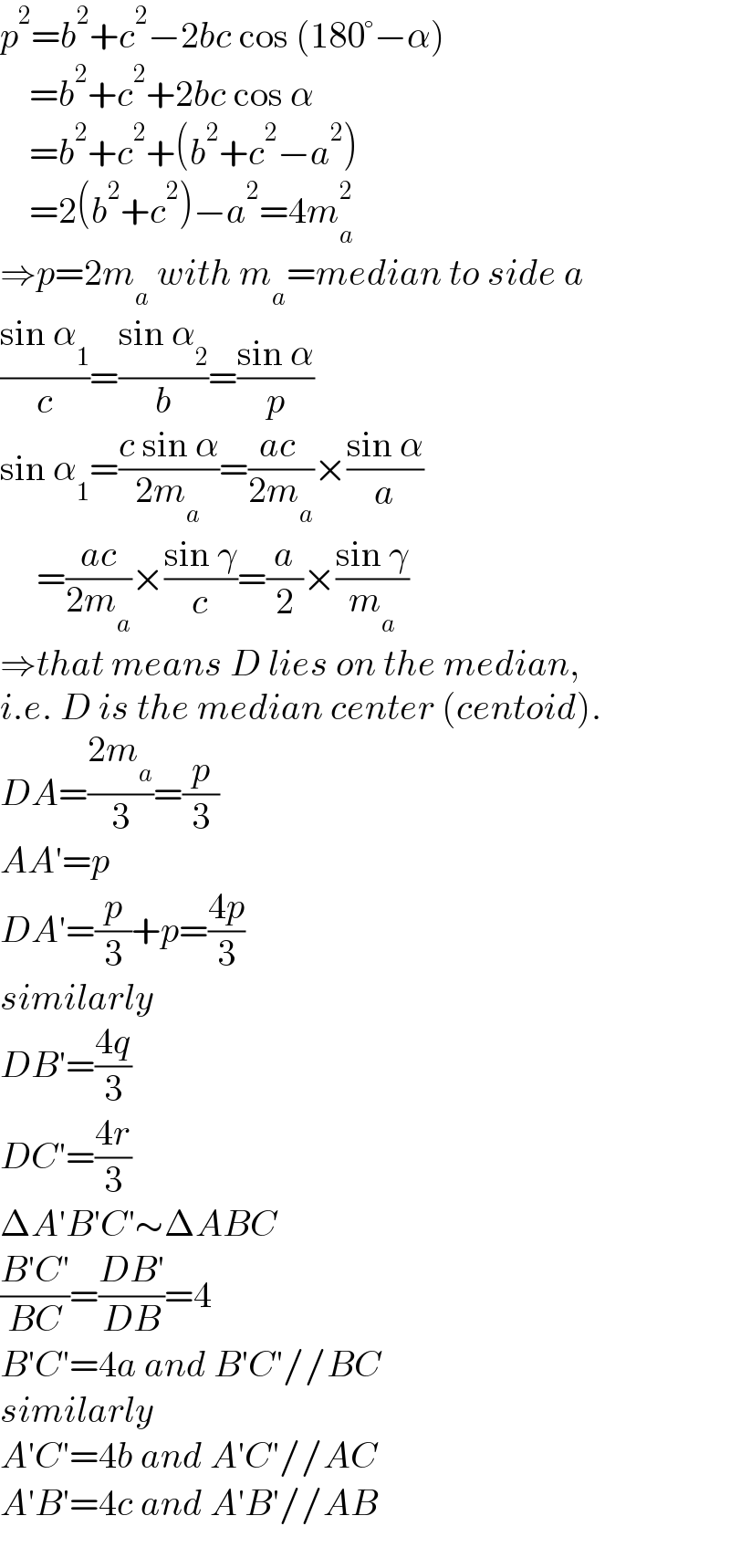 | ||