Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 180977 by mr W last updated on 19/Nov/22

what is larger, 3^(100) +4^(100) or 5^(100) ?

$${what}\:{is}\:{larger},\:\mathrm{3}^{\mathrm{100}} +\mathrm{4}^{\mathrm{100}} \:{or}\:\:\mathrm{5}^{\mathrm{100}} ? \\ $$

Answered by MJS_new last updated on 19/Nov/22

2×4^x <>^(?) 5^x 2^(2x+1) <>^(?) 5^x 2^(2+(1/x)) <>^(?) 5 (2)^(1/x) <>^(?) (5/4) (2)^(1/(100)) <1.25≈(2)^(1/3) ⇒ 2×4^(100) <5^(100) ⇒ 3^(100) +4^(100) <5^(100)

$$\mathrm{2}×\mathrm{4}^{{x}} \overset{?} {<>}\mathrm{5}^{{x}} \\ $$$$\mathrm{2}^{\mathrm{2}{x}+\mathrm{1}} \overset{?} {<>}\mathrm{5}^{{x}} \\ $$$$\mathrm{2}^{\mathrm{2}+\frac{\mathrm{1}}{{x}}} \overset{?} {<>}\mathrm{5} \\ $$$$\sqrt[{{x}}]{\mathrm{2}}\overset{?} {<>}\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\sqrt[{\mathrm{100}}]{\mathrm{2}}<\mathrm{1}.\mathrm{25}\approx\sqrt[{\mathrm{3}}]{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{2}×\mathrm{4}^{\mathrm{100}} <\mathrm{5}^{\mathrm{100}} \:\Rightarrow\:\mathrm{3}^{\mathrm{100}} +\mathrm{4}^{\mathrm{100}} <\mathrm{5}^{\mathrm{100}} \\ $$

Commented by MJS_new last updated on 20/Nov/22

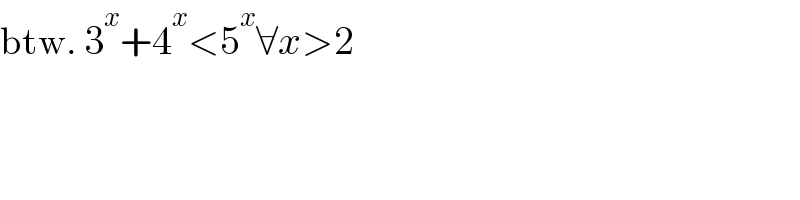
btw. 3^x +4^x <5^x ∀x>2

$$\mathrm{btw}.\:\mathrm{3}^{{x}} +\mathrm{4}^{{x}} <\mathrm{5}^{{x}} \forall{x}>\mathrm{2} \\ $$

Answered by manxsol last updated on 20/Nov/22

for induccion matematica n=1 3^1 +4^1 ⟩5^1 V n=k 3^k +4^k ⟩5^k suposicion V entonces n=k+1 must be V comprobacion n=k+1 3^(k+1) +4^(k+1) ⟩5^(k+1) 3.3^k +4.4^k ⟩5.5^k 3.3^k +3.4^k +4^k ⟩5.5^k 3(3^k +4^k )⟩3.5^k ver n=k 3(3^k +4^k )+4^k ⟩3.5^k +4^k ⟩5.5^k 4^k ⟩2.5^k is False ⇒3^(100) +4^(100) ⟨ 5^(100)

$${for}\:{induccion}\:{matematica} \\ $$$${n}=\mathrm{1}\:\:\:\mathrm{3}^{\mathrm{1}} +\mathrm{4}^{\mathrm{1}} \rangle\mathrm{5}^{\mathrm{1}} \:\:\:\:\:\:\:\:{V} \\ $$$${n}={k}\:\:\:\mathrm{3}^{{k}} +\mathrm{4}^{{k}} \rangle\mathrm{5}^{{k}} \:\:\:\:{suposicion}\:{V} \\ $$$${entonces} \\ $$$${n}={k}+\mathrm{1}\:\:\:{must}\:{be}\:\:{V} \\ $$$${comprobacion} \\ $$$${n}={k}+\mathrm{1}\:\:\:\:\:\mathrm{3}^{{k}+\mathrm{1}} +\mathrm{4}^{{k}+\mathrm{1}} \rangle\mathrm{5}^{{k}+\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}.\mathrm{3}^{{k}} +\mathrm{4}.\mathrm{4}^{{k}} \rangle\mathrm{5}.\mathrm{5}^{{k}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}.\mathrm{3}^{{k}} +\mathrm{3}.\mathrm{4}^{{k}} +\mathrm{4}^{{k}} \rangle\mathrm{5}.\mathrm{5}^{{k}} \\ $$$$\:\:\:\:\:\:\mathrm{3}\left(\mathrm{3}^{{k}} +\mathrm{4}^{{k}} \right)\rangle\mathrm{3}.\mathrm{5}^{{k}} \:\:\:\:{ver}\:{n}={k} \\ $$$$\:\:\:\:\:\:\mathrm{3}\left(\mathrm{3}^{{k}} +\mathrm{4}^{{k}} \right)+\mathrm{4}^{{k}} \rangle\mathrm{3}.\mathrm{5}^{{k}} +\mathrm{4}^{{k}} \rangle\mathrm{5}.\mathrm{5}^{{k}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}^{{k}} \rangle\mathrm{2}.\mathrm{5}^{{k}} \:{is}\:{False} \\ $$$$\Rightarrow\mathrm{3}^{\mathrm{100}} +\mathrm{4}^{\mathrm{100}} \langle\:\mathrm{5}^{\mathrm{100}} \\ $$$$ \\ $$

Commented by mr W last updated on 20/Nov/22

thanks sirs!

$${thanks}\:{sirs}! \\ $$

Answered by mr W last updated on 20/Nov/22

an other way recall: for 0<a<1, a^x is strictly decreasing, i.e. a^(100) <a^(99) <...<a^2 . ((3^(100) +4^(100) )/5^(100) )=0.6^(100) +0.8^(100) <0.6^2 +0.8^2 =0.36+0.64=1 ⇒3^(100) +4^(100) <5^(100)

$${an}\:{other}\:{way} \\ $$$${recall}:\: \\ $$$${for}\:\mathrm{0}<{a}<\mathrm{1},\:{a}^{{x}} \:{is}\:{strictly}\:{decreasing},\:{i}.{e}. \\ $$$${a}^{\mathrm{100}} <{a}^{\mathrm{99}} <...<{a}^{\mathrm{2}} . \\ $$$$\frac{\mathrm{3}^{\mathrm{100}} +\mathrm{4}^{\mathrm{100}} }{\mathrm{5}^{\mathrm{100}} }=\mathrm{0}.\mathrm{6}^{\mathrm{100}} +\mathrm{0}.\mathrm{8}^{\mathrm{100}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:<\mathrm{0}.\mathrm{6}^{\mathrm{2}} +\mathrm{0}.\mathrm{8}^{\mathrm{2}} =\mathrm{0}.\mathrm{36}+\mathrm{0}.\mathrm{64}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{3}^{\mathrm{100}} +\mathrm{4}^{\mathrm{100}} <\mathrm{5}^{\mathrm{100}} \\ $$

Commented by manxsol last updated on 20/Nov/22

great way

$${great}\:{way} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com