Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 181055 by Acem last updated on 21/Nov/22

Commented by Acem last updated on 21/Nov/22

∗ DABC Please, the comments section is only for inquiries and clarifications

$$\ast\:{DABC} \\ $$$${Please},\:{the}\:{comments}\:{section}\:{is}\:{only} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{for} \\ $$$$\:\:\:\:\:\boldsymbol{{inquiries}}\:\boldsymbol{{and}}\:\boldsymbol{{clarifications}} \\ $$$$ \\ $$

Commented by som(math1967) last updated on 21/Nov/22

Commented by som(math1967) last updated on 21/Nov/22

∠DOA=2∠DLA so O is centre of circumcircle of △LDA OD=OA=((10)/( (√2)))=5(√2) CB∥DA ∴△ ODA∼△OBC ((OB)/(OD))=((BC)/(DA))=(4/(10)) ⇒OB=(2/5)×5(√2)=2(√2) ar of DABC=△AOD+△AOB +△BOC+△DOC =(1/2)×5(√2)×5(√2)+(1/2)×2(√2)×5(√2) +(1/2)×2(√2)×2(√2)+(1/2)×2(√2)×5(√2) =25+10+4+10=49 squnit

$$\angle{DOA}=\mathrm{2}\angle{DLA} \\ $$$${so}\:{O}\:{is}\:{centre}\:{of}\:{circumcircle}\:{of} \\ $$$$\bigtriangleup{LDA}\:\:{OD}={OA}=\frac{\mathrm{10}}{\:\sqrt{\mathrm{2}}}=\mathrm{5}\sqrt{\mathrm{2}} \\ $$$${CB}\parallel{DA}\:\therefore\bigtriangleup\:{ODA}\sim\bigtriangleup{OBC} \\ $$$$\:\:\frac{{OB}}{{OD}}=\frac{{BC}}{{DA}}=\frac{\mathrm{4}}{\mathrm{10}} \\ $$$$\Rightarrow{OB}=\frac{\mathrm{2}}{\mathrm{5}}×\mathrm{5}\sqrt{\mathrm{2}}=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$${ar}\:{of}\:{DABC}=\bigtriangleup{AOD}+\bigtriangleup{AOB} \\ $$$$+\bigtriangleup{BOC}+\bigtriangleup{DOC} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{5}\sqrt{\mathrm{2}}×\mathrm{5}\sqrt{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}\sqrt{\mathrm{2}}×\mathrm{5}\sqrt{\mathrm{2}} \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}\sqrt{\mathrm{2}}×\mathrm{2}\sqrt{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}\sqrt{\mathrm{2}}×\mathrm{5}\sqrt{\mathrm{2}} \\ $$$$=\mathrm{25}+\mathrm{10}+\mathrm{4}+\mathrm{10}=\mathrm{49}\:{squnit} \\ $$

Commented by mr W last updated on 21/Nov/22

Acem sir: with angle 45°, the trangle and the trapazoid are symmetric, and the solution is obvious. we can get the result directly as som sir did. if the angle is 60°, we can′t get the result obviously as with 45°. with 45°, the diagonals of the trapazoid are equal and equal to (5+2)(√2)=7(√2). the area of the trapazoid is then ((7(√2)×7(√2))/2)=49. with angle 60°, we can′t get it so obviously.

$${Acem}\:{sir}:\:{with}\:{angle}\:\mathrm{45}°,\:{the}\:{trangle} \\ $$$${and}\:{the}\:{trapazoid}\:{are}\:{symmetric}, \\ $$$${and}\:{the}\:{solution}\:{is}\:{obvious}.\:{we}\:{can} \\ $$$${get}\:{the}\:{result}\:{directly}\:{as}\:{som}\:{sir}\:{did}. \\ $$$${if}\:{the}\:{angle}\:{is}\:\mathrm{60}°,\:{we}\:{can}'{t}\:{get}\:{the} \\ $$$${result}\:{obviously}\:{as}\:{with}\:\mathrm{45}°. \\ $$$${with}\:\mathrm{45}°,\:{the}\:{diagonals}\:{of}\:{the}\:{trapazoid} \\ $$$${are}\:{equal}\:{and}\:{equal}\:{to}\:\left(\mathrm{5}+\mathrm{2}\right)\sqrt{\mathrm{2}}=\mathrm{7}\sqrt{\mathrm{2}}. \\ $$$${the}\:{area}\:{of}\:{the}\:{trapazoid}\:{is}\:{then} \\ $$$$\frac{\mathrm{7}\sqrt{\mathrm{2}}×\mathrm{7}\sqrt{\mathrm{2}}}{\mathrm{2}}=\mathrm{49}. \\ $$$${with}\:{angle}\:\mathrm{60}°,\:{we}\:{can}'{t}\:{get}\:{it}\:{so} \\ $$$${obviously}. \\ $$

Commented by Acem last updated on 21/Nov/22

What if D or A was out of the circle? In other word, we can form infinite number of trapezoids with 2 parallel bases. And please copy all your solutions to buffer from the menu ⋮and paste copied buffer as answer part, then please remove the comments. Thanks friend!

$${What}\:{if}\:{D}\:{or}\:{A}\:{was}\:{out}\:{of}\:{the}\:{circle}? \\ $$$$\:{In}\:{other}\:{word},\:{we}\:{can}\:{form}\:{infinite}\:{number}\:{of}\: \\ $$$$\:{trapezoids}\:{with}\:\mathrm{2}\:{parallel}\:{bases}. \\ $$$$ \\ $$$${And}\:{please}\:{copy}\:{all}\:{your}\:{solutions}\:{to}\:{buffer}\:{from} \\ $$$$\:{the}\:{menu}\:\vdots{and}\:{paste}\:{copied}\:{buffer}\:{as}\:{answer} \\ $$$$\:{part},\:{then}\:{please}\:{remove}\:{the}\:{comments}. \\ $$$$\:{Thanks}\:{friend}! \\ $$

Commented by mr W last updated on 21/Nov/22

the angle 45° makes the thing to a special case which is too obvious. it′s more interesting when the angle is not 45°, but e.g. 60°.

$${the}\:{angle}\:\mathrm{45}°\:{makes}\:{the}\:{thing}\:{to}\:{a} \\ $$$${special}\:{case}\:{which}\:{is}\:{too}\:{obvious}.\: \\ $$$${it}'{s}\:{more}\:{interesting}\:{when}\:{the}\:{angle} \\ $$$${is}\:{not}\:\mathrm{45}°,\:{but}\:{e}.{g}.\:\mathrm{60}°. \\ $$

Commented by mr W last updated on 21/Nov/22

the solution above from som sir is wonderful!

$${the}\:{solution}\:{above}\:{from}\:{som}\:{sir}\:{is}\: \\ $$$${wonderful}! \\ $$

Commented by Acem last updated on 21/Nov/22

No problem Sir Som

$${No}\:{problem}\:{Sir}\:{Som} \\ $$

Commented by Acem last updated on 21/Nov/22

With an angle 45 is more interesting than 60

$${With}\:{an}\:{angle}\:\mathrm{45}\:{is}\:{more}\:{interesting}\:{than}\:\mathrm{60} \\ $$$$ \\ $$

Commented by som(math1967) last updated on 21/Nov/22

sorry cannot load as answer

$${sorry}\:{cannot}\:{load}\:{as}\:{answer}\: \\ $$

Commented by MJS_new last updated on 21/Nov/22

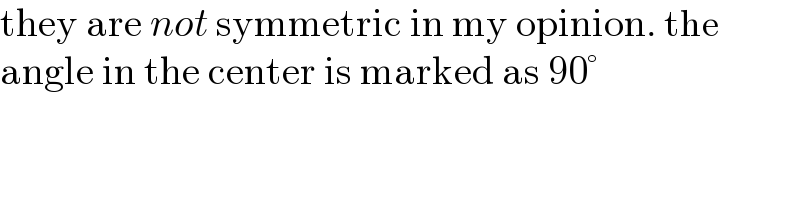
they are not symmetric in my opinion. the angle in the center is marked as 90°

$$\mathrm{they}\:\mathrm{are}\:{not}\:\mathrm{symmetric}\:\mathrm{in}\:\mathrm{my}\:\mathrm{opinion}.\:\mathrm{the} \\ $$$$\mathrm{angle}\:\mathrm{in}\:\mathrm{the}\:\mathrm{center}\:\mathrm{is}\:\mathrm{marked}\:\mathrm{as}\:\mathrm{90}° \\ $$

Commented by mr W last updated on 21/Nov/22

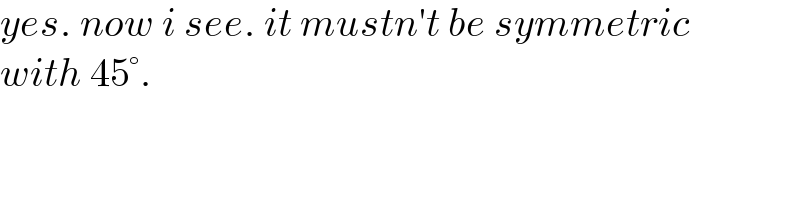
yes. now i see. it mustn′t be symmetric with 45°.

$${yes}.\:{now}\:{i}\:{see}.\:{it}\:{mustn}'{t}\:{be}\:{symmetric} \\ $$$${with}\:\mathrm{45}°. \\ $$

Commented by MJS_new last updated on 21/Nov/22

the difference is not visible in the drawing. with a base length 10 and an angle of 45° between the bottom l line and the diagonals we don′t get length 4 for the shorter horizontal line but 10((√2)−1)≈4.14

$$\mathrm{the}\:\mathrm{difference}\:\mathrm{is}\:\mathrm{not}\:\mathrm{visible}\:\mathrm{in}\:\mathrm{the}\:\mathrm{drawing}. \\ $$$$\mathrm{with}\:\mathrm{a}\:\mathrm{base}\:\mathrm{length}\:\mathrm{10}\:\mathrm{and}\:\mathrm{an}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{45}° \\ $$$$\mathrm{between}\:\mathrm{the}\:\mathrm{bottom} \\ $$$$\mathrm{l}\:\mathrm{line}\:\mathrm{and}\:\mathrm{the}\:\mathrm{diagonals}\:\mathrm{we}\:\mathrm{don}'\mathrm{t}\:\mathrm{get}\:\mathrm{length} \\ $$$$\mathrm{4}\:\mathrm{for}\:\mathrm{the}\:\mathrm{shorter}\:\mathrm{horizontal}\:\mathrm{line}\:\mathrm{but} \\ $$$$\mathrm{10}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\approx\mathrm{4}.\mathrm{14} \\ $$

Commented by mr W last updated on 21/Nov/22

yes sir! i saw this contradiction very late. i think, it is symmetric only when θ=46.397°.

$${yes}\:{sir}!\:{i}\:{saw}\:{this}\:{contradiction}\:{very} \\ $$$${late}.\:\:{i}\:{think},\:{it}\:{is}\:{symmetric}\:{only} \\ $$$${when}\:\theta=\mathrm{46}.\mathrm{397}°. \\ $$

Answered by MJS_new last updated on 21/Nov/22

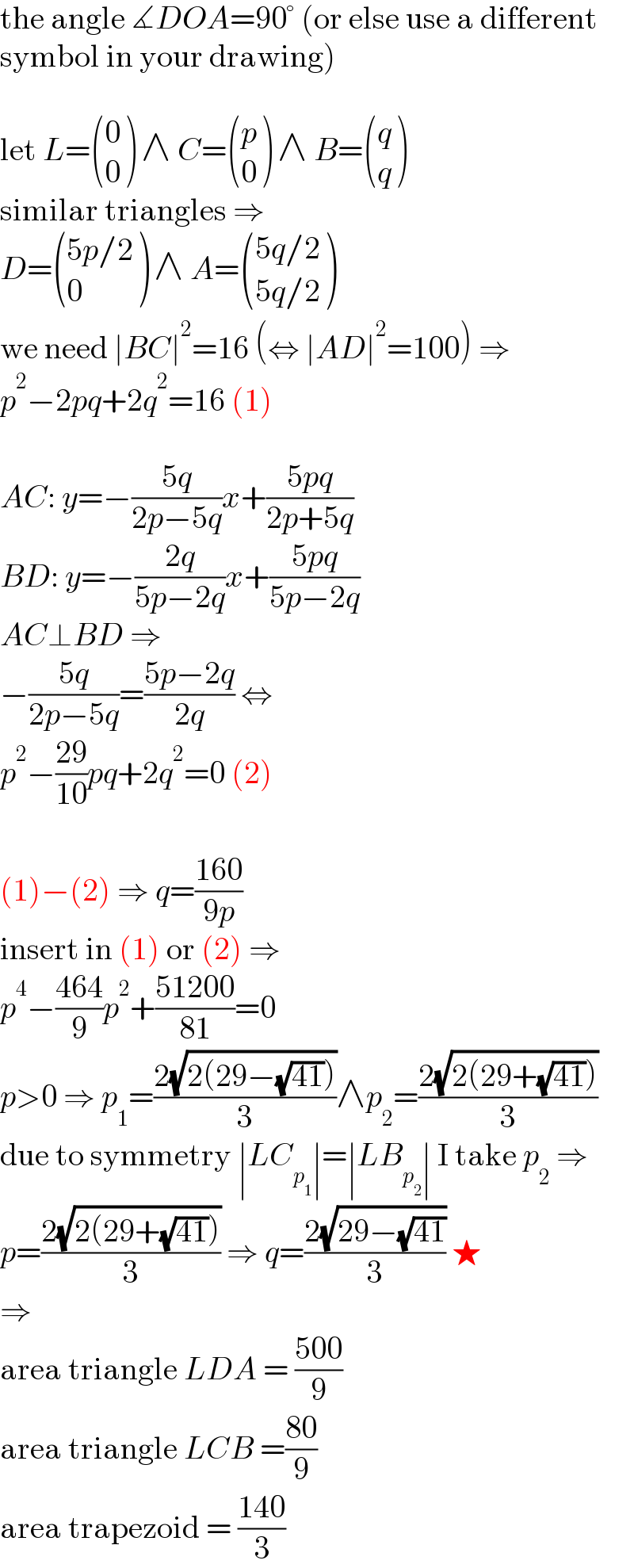
the angle ∡DOA=90° (or else use a different symbol in your drawing) let L= ((0),(0) ) ∧ C= ((p),(0) ) ∧ B= ((q),(q) ) similar triangles ⇒ D= (((5p/2)),(0) ) ∧ A= (((5q/2)),((5q/2)) ) we need ∣BC∣^2 =16 (⇔ ∣AD∣^2 =100) ⇒ p^2 −2pq+2q^2 =16 (1) AC: y=−((5q)/(2p−5q))x+((5pq)/(2p+5q)) BD: y=−((2q)/(5p−2q))x+((5pq)/(5p−2q)) AC⊥BD ⇒ −((5q)/(2p−5q))=((5p−2q)/(2q)) ⇔ p^2 −((29)/(10))pq+2q^2 =0 (2) (1)−(2) ⇒ q=((160)/(9p)) insert in (1) or (2) ⇒ p^4 −((464)/9)p^2 +((51200)/(81))=0 p>0 ⇒ p_1 =((2(√(2(29−(√(41))))))/3)∧p_2 =((2(√(2(29+(√(41))))))/3) due to symmetry ∣LC_p_1 ∣=∣LB_p_2 ∣ I take p_2 ⇒ p=((2(√(2(29+(√(41))))))/3) ⇒ q=((2(√(29−(√(41)))))/3) ★ ⇒ area triangle LDA = ((500)/9) area triangle LCB =((80)/9) area trapezoid = ((140)/3)

$$\mathrm{the}\:\mathrm{angle}\:\measuredangle{DOA}=\mathrm{90}°\:\left(\mathrm{or}\:\mathrm{else}\:\mathrm{use}\:\mathrm{a}\:\mathrm{different}\right. \\ $$$$\left.\mathrm{symbol}\:\mathrm{in}\:\mathrm{your}\:\mathrm{drawing}\right) \\ $$$$ \\ $$$$\mathrm{let}\:{L}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:\wedge\:{C}=\begin{pmatrix}{{p}}\\{\mathrm{0}}\end{pmatrix}\:\wedge\:{B}=\begin{pmatrix}{{q}}\\{{q}}\end{pmatrix} \\ $$$$\mathrm{similar}\:\mathrm{triangles}\:\Rightarrow \\ $$$${D}=\begin{pmatrix}{\mathrm{5}{p}/\mathrm{2}}\\{\mathrm{0}}\end{pmatrix}\:\wedge\:{A}=\begin{pmatrix}{\mathrm{5}{q}/\mathrm{2}}\\{\mathrm{5}{q}/\mathrm{2}}\end{pmatrix} \\ $$$$\mathrm{we}\:\mathrm{need}\:\mid{BC}\mid^{\mathrm{2}} =\mathrm{16}\:\left(\Leftrightarrow\:\mid{AD}\mid^{\mathrm{2}} =\mathrm{100}\right)\:\Rightarrow \\ $$$${p}^{\mathrm{2}} −\mathrm{2}{pq}+\mathrm{2}{q}^{\mathrm{2}} =\mathrm{16}\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$${AC}:\:{y}=−\frac{\mathrm{5}{q}}{\mathrm{2}{p}−\mathrm{5}{q}}{x}+\frac{\mathrm{5}{pq}}{\mathrm{2}{p}+\mathrm{5}{q}} \\ $$$${BD}:\:{y}=−\frac{\mathrm{2}{q}}{\mathrm{5}{p}−\mathrm{2}{q}}{x}+\frac{\mathrm{5}{pq}}{\mathrm{5}{p}−\mathrm{2}{q}} \\ $$$${AC}\bot{BD}\:\Rightarrow \\ $$$$−\frac{\mathrm{5}{q}}{\mathrm{2}{p}−\mathrm{5}{q}}=\frac{\mathrm{5}{p}−\mathrm{2}{q}}{\mathrm{2}{q}}\:\Leftrightarrow \\ $$$${p}^{\mathrm{2}} −\frac{\mathrm{29}}{\mathrm{10}}{pq}+\mathrm{2}{q}^{\mathrm{2}} =\mathrm{0}\:\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\left(\mathrm{1}\right)−\left(\mathrm{2}\right)\:\Rightarrow\:{q}=\frac{\mathrm{160}}{\mathrm{9}{p}} \\ $$$$\mathrm{insert}\:\mathrm{in}\:\left(\mathrm{1}\right)\:\mathrm{or}\:\left(\mathrm{2}\right)\:\Rightarrow \\ $$$${p}^{\mathrm{4}} −\frac{\mathrm{464}}{\mathrm{9}}{p}^{\mathrm{2}} +\frac{\mathrm{51200}}{\mathrm{81}}=\mathrm{0} \\ $$$${p}>\mathrm{0}\:\Rightarrow\:{p}_{\mathrm{1}} =\frac{\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{29}−\sqrt{\mathrm{41}}\right)}}{\mathrm{3}}\wedge{p}_{\mathrm{2}} =\frac{\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{29}+\sqrt{\mathrm{41}}\right)}}{\mathrm{3}} \\ $$$$\mathrm{due}\:\mathrm{to}\:\mathrm{symmetry}\:\mid{LC}_{{p}_{\mathrm{1}} } \mid=\mid{LB}_{{p}_{\mathrm{2}} } \mid\:\mathrm{I}\:\mathrm{take}\:{p}_{\mathrm{2}} \:\Rightarrow \\ $$$${p}=\frac{\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{29}+\sqrt{\mathrm{41}}\right)}}{\mathrm{3}}\:\Rightarrow\:{q}=\frac{\mathrm{2}\sqrt{\mathrm{29}−\sqrt{\mathrm{41}}}}{\mathrm{3}}\:\bigstar \\ $$$$\Rightarrow \\ $$$$\mathrm{area}\:\mathrm{triangle}\:{LDA}\:=\:\frac{\mathrm{500}}{\mathrm{9}} \\ $$$$\mathrm{area}\:\mathrm{triangle}\:{LCB}\:=\frac{\mathrm{80}}{\mathrm{9}} \\ $$$$\mathrm{area}\:\mathrm{trapezoid}\:=\:\frac{\mathrm{140}}{\mathrm{3}} \\ $$

Commented by Acem last updated on 21/Nov/22

Very well work Sir! You can check the other method bellow Thanks!

$${Very}\:{well}\:{work}\:{Sir}! \\ $$$$\:{You}\:{can}\:{check}\:{the}\:{other}\:{method}\:{bellow} \\ $$$${Thanks}! \\ $$

Answered by Acem last updated on 21/Nov/22

Commented by Acem last updated on 21/Nov/22

We have ad= ((40)/(21)) & 4d^2 + 4a^2 = 16 by common solution: 441 d^( 4) −1764 d^( 2) + 1600= 0 we will find 2 solutions a_1 ≈ 1.17905 d_1 ≈ 1.6155 a_2 ≈ 1.6155 d_2 ≈ 1.17905 For example we take the 2nd one: AM= 5d ≈ 5.895 DM= 5a ≈ 8.077 they are not equal The circle of M as center with r= AM, the vertices D and F will be both out of it.

$${We}\:{have}\:{ad}=\:\frac{\mathrm{40}}{\mathrm{21}}\:\&\:\mathrm{4}{d}^{\mathrm{2}} +\:\mathrm{4}{a}^{\mathrm{2}} =\:\mathrm{16} \\ $$$$\:{by}\:{common}\:{solution}: \\ $$$$\:\:\:\:\:\mathrm{441}\:{d}^{\:\mathrm{4}} \:−\mathrm{1764}\:{d}^{\:\mathrm{2}} \:+\:\mathrm{1600}=\:\mathrm{0} \\ $$$$ \\ $$$$\:{we}\:{will}\:{find}\:\mathrm{2}\:{solutions} \\ $$$$\:{a}_{\mathrm{1}} \approx\:\mathrm{1}.\mathrm{17905}\:\:\:\:{d}_{\mathrm{1}} \approx\:\mathrm{1}.\mathrm{6155} \\ $$$$\:{a}_{\mathrm{2}} \approx\:\mathrm{1}.\mathrm{6155}\:\:\:\:\:\:\:{d}_{\mathrm{2}} \approx\:\mathrm{1}.\mathrm{17905} \\ $$$$\:{For}\:{example}\:{we}\:{take}\:{the}\:\mathrm{2}{nd}\:{one}: \\ $$$$\:{AM}=\:\mathrm{5}{d}\:\approx\:\mathrm{5}.\mathrm{895} \\ $$$$\:{DM}=\:\mathrm{5}{a}\:\approx\:\mathrm{8}.\mathrm{077}\:\:\:\:\:\:\:\:{they}\:{are}\:{not}\:{equal} \\ $$$$ \\ $$$$\:{The}\:{circle}\:{of}\:{M}\:{as}\:{center}\:{with}\:{r}=\:{AM}, \\ $$$$\:{the}\:{vertices}\:{D}\:{and}\:{F}\:{will}\:{be}\:{both}\:{out}\:{of}\:{it}. \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com