Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 181079 by Agnibhoo98 last updated on 21/Nov/22

Solve for x : (((x + a)/(x + b)))^3 = ((x + 2a − b)/(x − a + 2b))

$$\mathrm{Solve}\:\mathrm{for}\:{x}\:: \\ $$$$\left(\frac{{x}\:+\:{a}}{{x}\:+\:{b}}\right)^{\mathrm{3}} =\:\frac{{x}\:+\:\mathrm{2}{a}\:−\:{b}}{{x}\:−\:{a}\:+\:\mathrm{2}{b}} \\ $$

Commented by CElcedricjunior last updated on 21/Nov/22

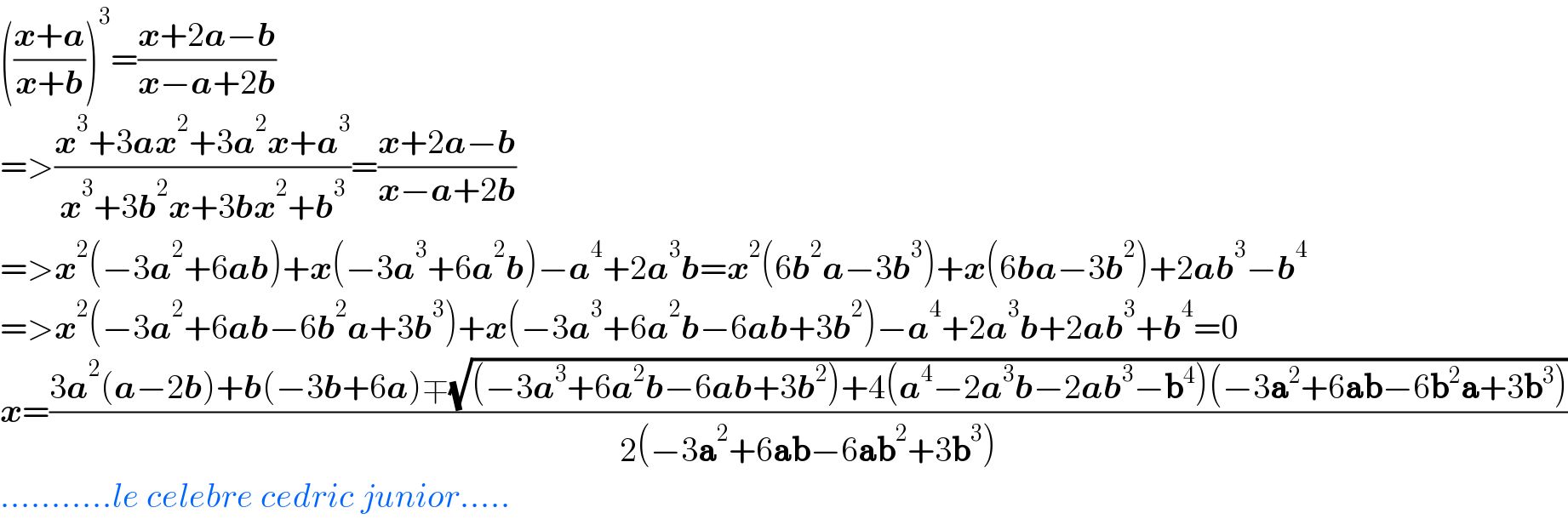
(((x+a)/(x+b)))^3 =((x+2a−b)/(x−a+2b)) =>((x^3 +3ax^2 +3a^2 x+a^3 )/(x^3 +3b^2 x+3bx^2 +b^3 ))=((x+2a−b)/(x−a+2b)) =>x^2 (−3a^2 +6ab)+x(−3a^3 +6a^2 b)−a^4 +2a^3 b=x^2 (6b^2 a−3b^3 )+x(6ba−3b^2 )+2ab^3 −b^4 =>x^2 (−3a^2 +6ab−6b^2 a+3b^3 )+x(−3a^3 +6a^2 b−6ab+3b^2 )−a^4 +2a^3 b+2ab^3 +b^4 =0 x=((3a^2 (a−2b)+b(−3b+6a)∓(√((−3a^3 +6a^2 b−6ab+3b^2 )+4(a^4 −2a^3 b−2ab^3 −b^4 )(−3a^2 +6ab−6b^2 a+3b^3 ))))/(2(−3a^2 +6ab−6ab^2 +3b^3 ))) ...........le celebre cedric junior.....

$$\left(\frac{\boldsymbol{{x}}+\boldsymbol{{a}}}{\boldsymbol{{x}}+\boldsymbol{{b}}}\right)^{\mathrm{3}} =\frac{\boldsymbol{{x}}+\mathrm{2}\boldsymbol{{a}}−\boldsymbol{{b}}}{\boldsymbol{{x}}−\boldsymbol{{a}}+\mathrm{2}\boldsymbol{{b}}} \\ $$$$=>\frac{\boldsymbol{{x}}^{\mathrm{3}} +\mathrm{3}\boldsymbol{{ax}}^{\mathrm{2}} +\mathrm{3}\boldsymbol{{a}}^{\mathrm{2}} \boldsymbol{{x}}+\boldsymbol{{a}}^{\mathrm{3}} }{\boldsymbol{{x}}^{\mathrm{3}} +\mathrm{3}\boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{x}}+\mathrm{3}\boldsymbol{{bx}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{3}} }=\frac{\boldsymbol{{x}}+\mathrm{2}\boldsymbol{{a}}−\boldsymbol{{b}}}{\boldsymbol{{x}}−\boldsymbol{{a}}+\mathrm{2}\boldsymbol{{b}}} \\ $$$$=>\boldsymbol{{x}}^{\mathrm{2}} \left(−\mathrm{3}\boldsymbol{{a}}^{\mathrm{2}} +\mathrm{6}\boldsymbol{{ab}}\right)+\boldsymbol{{x}}\left(−\mathrm{3}\boldsymbol{{a}}^{\mathrm{3}} +\mathrm{6}\boldsymbol{{a}}^{\mathrm{2}} \boldsymbol{{b}}\right)−\boldsymbol{{a}}^{\mathrm{4}} +\mathrm{2}\boldsymbol{{a}}^{\mathrm{3}} \boldsymbol{{b}}=\boldsymbol{{x}}^{\mathrm{2}} \left(\mathrm{6}\boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{a}}−\mathrm{3}\boldsymbol{{b}}^{\mathrm{3}} \right)+\boldsymbol{{x}}\left(\mathrm{6}\boldsymbol{{ba}}−\mathrm{3}\boldsymbol{{b}}^{\mathrm{2}} \right)+\mathrm{2}\boldsymbol{{ab}}^{\mathrm{3}} −\boldsymbol{{b}}^{\mathrm{4}} \\ $$$$=>\boldsymbol{{x}}^{\mathrm{2}} \left(−\mathrm{3}\boldsymbol{{a}}^{\mathrm{2}} +\mathrm{6}\boldsymbol{{ab}}−\mathrm{6}\boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{a}}+\mathrm{3}\boldsymbol{{b}}^{\mathrm{3}} \right)+\boldsymbol{{x}}\left(−\mathrm{3}\boldsymbol{{a}}^{\mathrm{3}} +\mathrm{6}\boldsymbol{{a}}^{\mathrm{2}} \boldsymbol{{b}}−\mathrm{6}\boldsymbol{{ab}}+\mathrm{3}\boldsymbol{{b}}^{\mathrm{2}} \right)−\boldsymbol{{a}}^{\mathrm{4}} +\mathrm{2}\boldsymbol{{a}}^{\mathrm{3}} \boldsymbol{{b}}+\mathrm{2}\boldsymbol{{ab}}^{\mathrm{3}} +\boldsymbol{{b}}^{\mathrm{4}} =\mathrm{0} \\ $$$$\boldsymbol{{x}}=\frac{\mathrm{3}\boldsymbol{{a}}^{\mathrm{2}} \left(\boldsymbol{{a}}−\mathrm{2}\boldsymbol{{b}}\right)+\boldsymbol{{b}}\left(−\mathrm{3}\boldsymbol{{b}}+\mathrm{6}\boldsymbol{{a}}\right)\mp\sqrt{\left(−\mathrm{3}\boldsymbol{{a}}^{\mathrm{3}} +\mathrm{6}\boldsymbol{{a}}^{\mathrm{2}} \boldsymbol{{b}}−\mathrm{6}\boldsymbol{{ab}}+\mathrm{3}\boldsymbol{{b}}^{\mathrm{2}} \right)+\mathrm{4}\left(\boldsymbol{{a}}^{\mathrm{4}} −\mathrm{2}\boldsymbol{{a}}^{\mathrm{3}} \boldsymbol{{b}}−\mathrm{2}\boldsymbol{{ab}}^{\mathrm{3}} −\boldsymbol{\mathrm{b}}^{\mathrm{4}} \right)\left(−\mathrm{3}\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\mathrm{6}\boldsymbol{\mathrm{ab}}−\mathrm{6}\boldsymbol{\mathrm{b}}^{\mathrm{2}} \boldsymbol{\mathrm{a}}+\mathrm{3}\boldsymbol{\mathrm{b}}^{\mathrm{3}} \right)}}{\mathrm{2}\left(−\mathrm{3}\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\mathrm{6}\boldsymbol{\mathrm{ab}}−\mathrm{6}\boldsymbol{\mathrm{ab}}^{\mathrm{2}} +\mathrm{3}\boldsymbol{\mathrm{b}}^{\mathrm{3}} \right)} \\ $$$$...........{le}\:{celebre}\:{cedric}\:{junior}..... \\ $$

Commented by Frix last updated on 22/Nov/22

wrong.

$$\mathrm{wrong}. \\ $$

Answered by Rasheed.Sindhi last updated on 21/Nov/22

(((x+a)^3 )/((x+b)^3 ))=((x+2a−b)/(x−a+2b)) (p^3 /q^3 )=(u/v) ⇒((p^3 −q^3 )/(p^3 +q^3 ))=((u−v)/(u+v)) ⇒(((p−q)(p^2 +pq+q^2 ))/((p+q)(p^2 −pq+q^2 )))=((u−v)/(u+v)) p−q=x+a−x−b=a−b p+q=x+a+x+b=2x+a+b p^2 +pq+q^2 =(x^2 +2xa+a^2 )+(x^2 +(a+b)x+ab)+(x^2 +2xb+b^2 ) =3x^2 +3x(a+b)+a^2 +ab+b^2 p^2 −pq+q^2 =(x^2 +2xa+a^2 )−(x^2 +(a+b)x+ab)+(x^2 +2xb+b^2 ) =x^2 +x(a+b)+a^2 −ab+b^2 u−v=x+2a−b−x+a−2b=3(a−b) u+v=x+2a−b+x−a+2b=2x+a+b (((a−b)(3x^2 +x(a+b)+a^2 +ab+b^2 ))/((2x+a+b)(x^2 +x(a+b)+a^2 −ab+b^2 )))=((3(a−b))/(2x+a+b)) (((a−b)(3x^2 +3x(a+b)+a^2 +ab+b^2 ))/((2x+a+b)(3x^2 +x(a+b)+a^2 +ab+b^2 )))−((3(a−b))/(2x+a+b))=0 ((a−b)/(2x+a+b))(((3x^2 +3x(a+b)+a^2 +ab+b^2 )/(3x^2 +x(a+b)+a^2 +ab+b^2 ))−3)=0 ((a−b)/(2x+a+b^★ ))(((−6x^2 −2a^2 −2ab−2b^2 )/(x^2 +x(a+b)+a^2 −ab+b^(2★★) )))=0 a−b=0 ∣ −6x^2 −2a^2 −2ab−2b^2 =0 a=b ∣ 3x^2 =−(a^2 +ab+b^2 ) a=b ∣ x=±(√((−(a^2 +ab+b^2 ))/3)) ^★ 2x+a+b≠0⇒x≠−((a+b)/2) ^(★★) 3x^2 +x(a+b)+a^2 +ab+b^2 ≠0 x≠((−(a+b)±(√(a^2 +2ab+b^2 −12(a^2 +ab+b^2 ))))/6) ≠((−(a+b)±(√(−11a^2 −10ab−11b^2 )))/6)

$$\frac{\left({x}+{a}\right)^{\mathrm{3}} }{\left({x}+{b}\right)^{\mathrm{3}} }=\frac{{x}+\mathrm{2}{a}−{b}}{{x}−{a}+\mathrm{2}{b}} \\ $$$$\frac{{p}^{\mathrm{3}} }{{q}^{\mathrm{3}} }=\frac{{u}}{{v}} \\ $$$$\Rightarrow\frac{{p}^{\mathrm{3}} −{q}^{\mathrm{3}} }{{p}^{\mathrm{3}} +{q}^{\mathrm{3}} }=\frac{{u}−{v}}{{u}+{v}} \\ $$$$\Rightarrow\frac{\left({p}−{q}\right)\left({p}^{\mathrm{2}} +{pq}+{q}^{\mathrm{2}} \right)}{\left({p}+{q}\right)\left({p}^{\mathrm{2}} −{pq}+{q}^{\mathrm{2}} \right)}=\frac{{u}−{v}}{{u}+{v}} \\ $$$${p}−{q}={x}+{a}−{x}−{b}={a}−{b} \\ $$$${p}+{q}={x}+{a}+{x}+{b}=\mathrm{2}{x}+{a}+{b} \\ $$$${p}^{\mathrm{2}} +{pq}+{q}^{\mathrm{2}} =\left({x}^{\mathrm{2}} +\mathrm{2}{xa}+{a}^{\mathrm{2}} \right)+\left({x}^{\mathrm{2}} +\left({a}+{b}\right){x}+{ab}\right)+\left({x}^{\mathrm{2}} +\mathrm{2}{xb}+{b}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{x}\left({a}+{b}\right)+{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \\ $$$${p}^{\mathrm{2}} −{pq}+{q}^{\mathrm{2}} =\left({x}^{\mathrm{2}} +\mathrm{2}{xa}+{a}^{\mathrm{2}} \right)−\left({x}^{\mathrm{2}} +\left({a}+{b}\right){x}+{ab}\right)+\left({x}^{\mathrm{2}} +\mathrm{2}{xb}+{b}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} +{x}\left({a}+{b}\right)+{a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} \\ $$$${u}−{v}={x}+\mathrm{2}{a}−{b}−{x}+{a}−\mathrm{2}{b}=\mathrm{3}\left({a}−{b}\right) \\ $$$${u}+{v}={x}+\mathrm{2}{a}−{b}+{x}−{a}+\mathrm{2}{b}=\mathrm{2}{x}+{a}+{b} \\ $$$$\frac{\left({a}−{b}\right)\left(\mathrm{3}{x}^{\mathrm{2}} +{x}\left({a}+{b}\right)+{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right)}{\left(\mathrm{2}{x}+{a}+{b}\right)\left({x}^{\mathrm{2}} +{x}\left({a}+{b}\right)+{a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} \right)}=\frac{\mathrm{3}\left({a}−{b}\right)}{\mathrm{2}{x}+{a}+{b}} \\ $$$$\frac{\left({a}−{b}\right)\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{x}\left({a}+{b}\right)+{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right)}{\left(\mathrm{2}{x}+{a}+{b}\right)\left(\mathrm{3}{x}^{\mathrm{2}} +{x}\left({a}+{b}\right)+{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right)}−\frac{\mathrm{3}\left({a}−{b}\right)}{\mathrm{2}{x}+{a}+{b}}=\mathrm{0} \\ $$$$\frac{{a}−{b}}{\mathrm{2}{x}+{a}+{b}}\left(\frac{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{x}\left({a}+{b}\right)+{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} }{\mathrm{3}{x}^{\mathrm{2}} +{x}\left({a}+{b}\right)+{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} }−\mathrm{3}\right)=\mathrm{0} \\ $$$$\frac{{a}−{b}}{\mathrm{2}{x}+{a}+{b}^{\bigstar} }\left(\frac{−\mathrm{6}{x}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} −\mathrm{2}{ab}−\mathrm{2}{b}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{x}\left({a}+{b}\right)+{a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}\bigstar\bigstar} }\right)=\mathrm{0} \\ $$$${a}−{b}=\mathrm{0}\:\mid\:−\mathrm{6}{x}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} −\mathrm{2}{ab}−\mathrm{2}{b}^{\mathrm{2}} =\mathrm{0} \\ $$$${a}={b}\:\mid\:\mathrm{3}{x}^{\mathrm{2}} =−\left({a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right) \\ $$$${a}={b}\:\mid\:{x}=\pm\sqrt{\frac{−\left({a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right)}{\mathrm{3}}}\: \\ $$$$\:^{\bigstar} \mathrm{2}{x}+{a}+{b}\neq\mathrm{0}\Rightarrow{x}\neq−\frac{{a}+{b}}{\mathrm{2}} \\ $$$$\:^{\bigstar\bigstar} \mathrm{3}{x}^{\mathrm{2}} +{x}\left({a}+{b}\right)+{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \neq\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:{x}\neq\frac{−\left({a}+{b}\right)\pm\sqrt{{a}^{\mathrm{2}} +\mathrm{2}{ab}+{b}^{\mathrm{2}} −\mathrm{12}\left({a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right)}}{\mathrm{6}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\neq\frac{−\left({a}+{b}\right)\pm\sqrt{−\mathrm{11}{a}^{\mathrm{2}} −\mathrm{10}{ab}−\mathrm{11}{b}^{\mathrm{2}} }}{\mathrm{6}} \\ $$

Answered by MJS_new last updated on 21/Nov/22

x=−((a+b)/2)

$${x}=−\frac{{a}+{b}}{\mathrm{2}} \\ $$

Answered by mr W last updated on 21/Nov/22

if a=b: x∈R and x≠−a if a≠b: (((x+a)^3 )/((x+b)^3 ))=((x+a+(a−b))/(x+b−(a−b))) (x+a)^3 (x+b)−(a−b)(x+a)^3 =(x+b)^3 (x+a)+(a−b)(x+b)^3 (x+a)(x+b)[(x+a)^2 −(x+b)^2 ]=(a−b)(x+b)^3 +(a−b)(x+a)^3 (x+a)(x+b)[(x+a)+(x+b)]=(x+b)^3 +(x+a)^3 let u=x+a, v=x+b uv(u+v)=u^3 +v^3 =(u+v)(u^2 −uv+v^2 ) (u+v)(u−v)^2 =0 (2x+a+b)(a−b)^2 =0 ⇒2x+a+b=0 ⇒x=−((a+b)/2)

$${if}\:{a}={b}:\: \\ $$$${x}\in{R}\:{and}\:{x}\neq−{a} \\ $$$$ \\ $$$${if}\:{a}\neq{b}: \\ $$$$\frac{\left({x}+{a}\right)^{\mathrm{3}} }{\left({x}+{b}\right)^{\mathrm{3}} }=\frac{{x}+{a}+\left({a}−{b}\right)}{{x}+{b}−\left({a}−{b}\right)} \\ $$$$\left({x}+{a}\right)^{\mathrm{3}} \left({x}+{b}\right)−\left({a}−{b}\right)\left({x}+{a}\right)^{\mathrm{3}} =\left({x}+{b}\right)^{\mathrm{3}} \left({x}+{a}\right)+\left({a}−{b}\right)\left({x}+{b}\right)^{\mathrm{3}} \\ $$$$\left({x}+{a}\right)\left({x}+{b}\right)\left[\left({x}+{a}\right)^{\mathrm{2}} −\left({x}+{b}\right)^{\mathrm{2}} \right]=\left({a}−{b}\right)\left({x}+{b}\right)^{\mathrm{3}} +\left({a}−{b}\right)\left({x}+{a}\right)^{\mathrm{3}} \\ $$$$\left({x}+{a}\right)\left({x}+{b}\right)\left[\left({x}+{a}\right)+\left({x}+{b}\right)\right]=\left({x}+{b}\right)^{\mathrm{3}} +\left({x}+{a}\right)^{\mathrm{3}} \\ $$$${let}\:{u}={x}+{a},\:{v}={x}+{b} \\ $$$${uv}\left({u}+{v}\right)={u}^{\mathrm{3}} +{v}^{\mathrm{3}} =\left({u}+{v}\right)\left({u}^{\mathrm{2}} −{uv}+{v}^{\mathrm{2}} \right) \\ $$$$\left({u}+{v}\right)\left({u}−{v}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{2}{x}+{a}+{b}\right)\left({a}−{b}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{x}+{a}+{b}=\mathrm{0}\:\Rightarrow{x}=−\frac{{a}+{b}}{\mathrm{2}} \\ $$

Answered by Frix last updated on 22/Nov/22

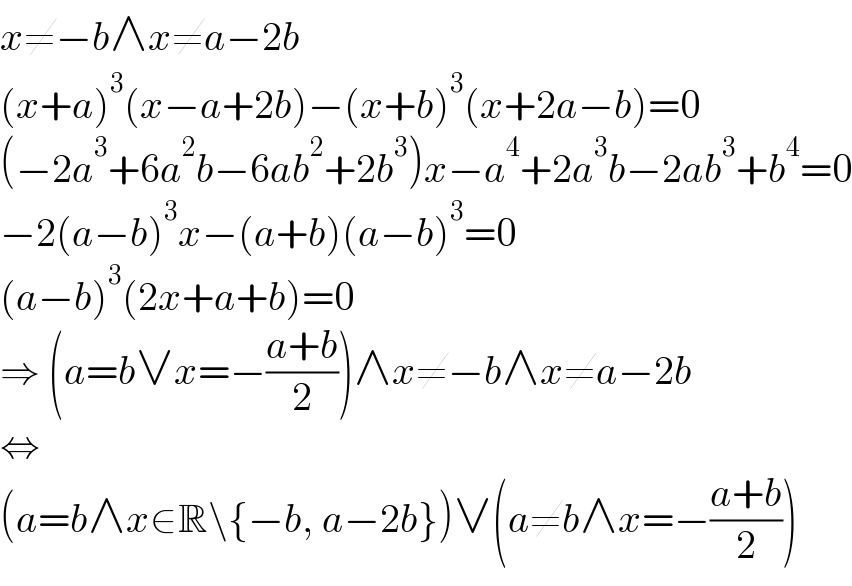
x≠−b∧x≠a−2b (x+a)^3 (x−a+2b)−(x+b)^3 (x+2a−b)=0 (−2a^3 +6a^2 b−6ab^2 +2b^3 )x−a^4 +2a^3 b−2ab^3 +b^4 =0 −2(a−b)^3 x−(a+b)(a−b)^3 =0 (a−b)^3 (2x+a+b)=0 ⇒ (a=b∨x=−((a+b)/2))∧x≠−b∧x≠a−2b ⇔ (a=b∧x∈R\{−b, a−2b})∨(a≠b∧x=−((a+b)/2))

$${x}\neq−{b}\wedge{x}\neq{a}−\mathrm{2}{b} \\ $$$$\left({x}+{a}\right)^{\mathrm{3}} \left({x}−{a}+\mathrm{2}{b}\right)−\left({x}+{b}\right)^{\mathrm{3}} \left({x}+\mathrm{2}{a}−{b}\right)=\mathrm{0} \\ $$$$\left(−\mathrm{2}{a}^{\mathrm{3}} +\mathrm{6}{a}^{\mathrm{2}} {b}−\mathrm{6}{ab}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{3}} \right){x}−{a}^{\mathrm{4}} +\mathrm{2}{a}^{\mathrm{3}} {b}−\mathrm{2}{ab}^{\mathrm{3}} +{b}^{\mathrm{4}} =\mathrm{0} \\ $$$$−\mathrm{2}\left({a}−{b}\right)^{\mathrm{3}} {x}−\left({a}+{b}\right)\left({a}−{b}\right)^{\mathrm{3}} =\mathrm{0} \\ $$$$\left({a}−{b}\right)^{\mathrm{3}} \left(\mathrm{2}{x}+{a}+{b}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\left({a}={b}\vee{x}=−\frac{{a}+{b}}{\mathrm{2}}\right)\wedge{x}\neq−{b}\wedge{x}\neq{a}−\mathrm{2}{b} \\ $$$$\Leftrightarrow \\ $$$$\left({a}={b}\wedge{x}\in\mathbb{R}\backslash\left\{−{b},\:{a}−\mathrm{2}{b}\right\}\right)\vee\left({a}\neq{b}\wedge{x}=−\frac{{a}+{b}}{\mathrm{2}}\right) \\ $$

Answered by manxsol last updated on 22/Nov/22

(((x+a)/(x+b)))^3 =((x+a+a−b)/( x+b−(a−b))) (((x+a)/(x+b)))^3 =(((x+a)+[(x+a)−(x+b)])/((x+b)−[(x+a)−(x−b)])) x+a=p x+b=q (p^3 /q^3 )=((2p−q)/(2q−p)) 2qp^3 −p^4 =2pq^3 −q^4 2qp(p^2 −q^2 )=p^4 −q^4 (p^2 −q^2 )(p^2 −2qp+q^2 )=0 (p−q)(p+q)(p−q)^2 =0 (p−q)^3 (p+q)=0 p=q⇒x+a=x+b⇒a=b p=−q⇒x+a^ =−x−b x=−(((a+b))/2) resumen determinant (((restriction),(solution)),((x≠{−b;a−2b}),(x=−((a+b)/2))),((a=b;x≠−b),(ℜ−{−b})))

$$\left(\frac{{x}+{a}}{{x}+\mathrm{b}}\right)^{\mathrm{3}} =\frac{\mathrm{x}+\mathrm{a}+\mathrm{a}−\mathrm{b}}{\:\mathrm{x}+\mathrm{b}−\left(\mathrm{a}−\mathrm{b}\right)} \\ $$$$\left(\frac{\mathrm{x}+\mathrm{a}}{\mathrm{x}+\mathrm{b}}\right)^{\mathrm{3}} =\frac{\left(\mathrm{x}+\mathrm{a}\right)+\left[\left(\mathrm{x}+\mathrm{a}\right)−\left(\mathrm{x}+\mathrm{b}\right)\right]}{\left(\mathrm{x}+\mathrm{b}\right)−\left[\left(\mathrm{x}+\mathrm{a}\right)−\left(\mathrm{x}−\mathrm{b}\right)\right]} \\ $$$$\mathrm{x}+\mathrm{a}=\mathrm{p} \\ $$$$\mathrm{x}+\mathrm{b}=\mathrm{q} \\ $$$$\frac{\mathrm{p}^{\mathrm{3}} }{\mathrm{q}^{\mathrm{3}} }=\frac{\mathrm{2p}−\mathrm{q}}{\mathrm{2q}−\mathrm{p}} \\ $$$$\mathrm{2qp}^{\mathrm{3}} −\mathrm{p}^{\mathrm{4}} =\mathrm{2pq}^{\mathrm{3}} −\mathrm{q}^{\mathrm{4}} \\ $$$$\mathrm{2qp}\left(\mathrm{p}^{\mathrm{2}} −\mathrm{q}^{\mathrm{2}} \right)=\mathrm{p}^{\mathrm{4}} −\mathrm{q}^{\mathrm{4}} \\ $$$$\left(\mathrm{p}^{\mathrm{2}} −\mathrm{q}^{\mathrm{2}} \right)\left(\mathrm{p}^{\mathrm{2}} −\mathrm{2qp}+{q}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\left(\mathrm{p}−\mathrm{q}\right)\left(\mathrm{p}+\mathrm{q}\right)\left(\mathrm{p}−\mathrm{q}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{p}−\mathrm{q}\right)^{\mathrm{3}} \left(\mathrm{p}+\mathrm{q}\right)=\mathrm{0} \\ $$$$\mathrm{p}=\mathrm{q}\Rightarrow{x}+{a}={x}+{b}\Rightarrow{a}={b} \\ $$$${p}=−{q}\Rightarrow{x}+\overset{} {{a}}=−{x}−{b} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}=−\frac{\left({a}+{b}\right)}{\mathrm{2}} \\ $$$${resumen} \\ $$$$\begin{array}{|c|c|c|}{{restriction}}&\hline{{solution}}\\{{x}\neq\left\{−{b};{a}−\mathrm{2}{b}\right\}}&\hline{{x}=−\frac{{a}+{b}}{\mathrm{2}}}\\{{a}={b};{x}\neq−{b}}&\hline{\Re−\left\{−{b}\right\}}\\\hline\end{array} \\ $$

Answered by Rasheed.Sindhi last updated on 22/Nov/22

(((x + a)/(x + b)))^3 = ((x + 2a − b)/(x − a + 2b)) ; x=? determinant (((A=((A+B)/2)+((A−B)/2) _(B=((A+B)/2)−((A−B)/2)^( ) ) ^( ) ))) •a=((a+b)/2)+((a−b)/2) •b=((a+b)/2)−((a−b)/2) •2a−b=(((2a−b)+(−a+2b))/2)+(((2a−b)−(−a+2b))/2) =((a+b)/2)+3(((a−b)/2)) •−a+2b=(((2a−b)+(−a+2b))/2)−(((2a−b)−(−a+2b))/2) =((a+b)/2)−3(((a−b)/2)) (((x+((a+b)/2)+((a−b)/2))^3 )/((x+((a+b)/2)−((a−b)/2))^3 ))=((x+((a+b)/2)+3(((a−b)/2)))/(x+((a+b)/2)−3(((a−b)/2)))) x+((a+b)/2)=y , ((a−b)/2)=k (((y+k)^3 )/((y−k)^3 ))=((y+3k)/(y−3k)) (((y+k)^2 )/((y−k)^2 ))=(((y−k)(y+3k))/((y+k)(y−3k))) ((y^2 +2ky+k^2 )/(y^2 −2ky+k^2 ))−1=((y^2 +2ky−3k^2 )/(y^2 −2ky−3k^2 ))−1 ((4ky)/(y^2 −2ky+k^2 ))=((4ky)/(y^2 −2ky−3k^2 )) (y/(y^2 −2ky+k^2 ))−(y/(y^2 −2ky−3k^2 ))=0 ;k≠0 y((1/(y^2 −2ky+k^2 ))−(1/(y^2 −2ky−3k^2 )))=0 y=0^★ ∣ (1/(y^2 −2ky+k^2 ))−(1/(y^2 −2ky−3k^2 ))=0^⧫ ^★ y=0⇒x+((a+b)/2)=0⇒x=−((a+b)/2) ^⧫ (1/(y^2 −2ky+k^2 ))−(1/(y^2 −2ky−3k^2 ))=0 (1/(y^2 −2ky+k^2 ))=(1/(y^2 −2ky−3k^2 )) y^2 ^(×) −2ky^(×) −3k^2 =y^2 ^(×) −2ky^(×) +k^2 4k^2 =0⇒k=0⇒((a−b)/2)=0⇒a=b

$$\left(\frac{{x}\:+\:{a}}{{x}\:+\:{b}}\right)^{\mathrm{3}} =\:\frac{{x}\:+\:\mathrm{2}{a}\:−\:{b}}{{x}\:−\:{a}\:+\:\mathrm{2}{b}}\:;\:{x}=? \\ $$$$\begin{array}{|c|}{\underset{\overset{\:} {{B}=\frac{{A}+{B}}{\mathrm{2}}−\frac{{A}−{B}}{\mathrm{2}}}} {\overset{\:} {{A}=\frac{{A}+{B}}{\mathrm{2}}+\frac{{A}−{B}}{\mathrm{2}}\:}}}\\\hline\end{array}\: \\ $$$$\bullet{a}=\frac{{a}+{b}}{\mathrm{2}}+\frac{{a}−{b}}{\mathrm{2}}\:\: \\ $$$$\bullet{b}=\frac{{a}+{b}}{\mathrm{2}}−\frac{{a}−{b}}{\mathrm{2}} \\ $$$$\bullet\mathrm{2}{a}−{b}=\frac{\left(\mathrm{2}{a}−{b}\right)+\left(−{a}+\mathrm{2}{b}\right)}{\mathrm{2}}+\frac{\left(\mathrm{2}{a}−{b}\right)−\left(−{a}+\mathrm{2}{b}\right)}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{a}+{b}}{\mathrm{2}}+\mathrm{3}\left(\frac{{a}−{b}}{\mathrm{2}}\right) \\ $$$$\bullet−{a}+\mathrm{2}{b}=\frac{\left(\mathrm{2}{a}−{b}\right)+\left(−{a}+\mathrm{2}{b}\right)}{\mathrm{2}}−\frac{\left(\mathrm{2}{a}−{b}\right)−\left(−{a}+\mathrm{2}{b}\right)}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{a}+{b}}{\mathrm{2}}−\mathrm{3}\left(\frac{{a}−{b}}{\mathrm{2}}\right) \\ $$$$\frac{\left({x}+\frac{{a}+{b}}{\mathrm{2}}+\frac{{a}−{b}}{\mathrm{2}}\right)^{\mathrm{3}} }{\left({x}+\frac{{a}+{b}}{\mathrm{2}}−\frac{{a}−{b}}{\mathrm{2}}\right)^{\mathrm{3}} }=\frac{{x}+\frac{{a}+{b}}{\mathrm{2}}+\mathrm{3}\left(\frac{{a}−{b}}{\mathrm{2}}\right)}{{x}+\frac{{a}+{b}}{\mathrm{2}}−\mathrm{3}\left(\frac{{a}−{b}}{\mathrm{2}}\right)} \\ $$$${x}+\frac{{a}+{b}}{\mathrm{2}}={y}\:,\:\frac{{a}−{b}}{\mathrm{2}}={k} \\ $$$$\frac{\left({y}+{k}\right)^{\mathrm{3}} }{\left({y}−{k}\right)^{\mathrm{3}} }=\frac{{y}+\mathrm{3}{k}}{{y}−\mathrm{3}{k}} \\ $$$$\frac{\left({y}+{k}\right)^{\mathrm{2}} }{\left({y}−{k}\right)^{\mathrm{2}} }=\frac{\left({y}−{k}\right)\left({y}+\mathrm{3}{k}\right)}{\left({y}+{k}\right)\left({y}−\mathrm{3}{k}\right)} \\ $$$$\frac{{y}^{\mathrm{2}} +\mathrm{2}{ky}+{k}^{\mathrm{2}} }{{y}^{\mathrm{2}} −\mathrm{2}{ky}+{k}^{\mathrm{2}} }−\mathrm{1}=\frac{{y}^{\mathrm{2}} +\mathrm{2}{ky}−\mathrm{3}{k}^{\mathrm{2}} }{{y}^{\mathrm{2}} −\mathrm{2}{ky}−\mathrm{3}{k}^{\mathrm{2}} }−\mathrm{1} \\ $$$$\frac{\mathrm{4}{ky}}{{y}^{\mathrm{2}} −\mathrm{2}{ky}+{k}^{\mathrm{2}} }=\frac{\mathrm{4}{ky}}{{y}^{\mathrm{2}} −\mathrm{2}{ky}−\mathrm{3}{k}^{\mathrm{2}} } \\ $$$$\frac{{y}}{{y}^{\mathrm{2}} −\mathrm{2}{ky}+{k}^{\mathrm{2}} }−\frac{{y}}{{y}^{\mathrm{2}} −\mathrm{2}{ky}−\mathrm{3}{k}^{\mathrm{2}} }=\mathrm{0}\:;{k}\neq\mathrm{0} \\ $$$${y}\left(\frac{\mathrm{1}}{{y}^{\mathrm{2}} −\mathrm{2}{ky}+{k}^{\mathrm{2}} }−\frac{\mathrm{1}}{{y}^{\mathrm{2}} −\mathrm{2}{ky}−\mathrm{3}{k}^{\mathrm{2}} }\right)=\mathrm{0} \\ $$$${y}=\mathrm{0}^{\bigstar} \:\mid\:\frac{\mathrm{1}}{{y}^{\mathrm{2}} −\mathrm{2}{ky}+{k}^{\mathrm{2}} }−\frac{\mathrm{1}}{{y}^{\mathrm{2}} −\mathrm{2}{ky}−\mathrm{3}{k}^{\mathrm{2}} }=\mathrm{0}^{\blacklozenge} \\ $$$$\:^{\bigstar} {y}=\mathrm{0}\Rightarrow{x}+\frac{{a}+{b}}{\mathrm{2}}=\mathrm{0}\Rightarrow{x}=−\frac{{a}+{b}}{\mathrm{2}} \\ $$$$\:^{\blacklozenge} \frac{\mathrm{1}}{{y}^{\mathrm{2}} −\mathrm{2}{ky}+{k}^{\mathrm{2}} }−\frac{\mathrm{1}}{{y}^{\mathrm{2}} −\mathrm{2}{ky}−\mathrm{3}{k}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\:\frac{\mathrm{1}}{{y}^{\mathrm{2}} −\mathrm{2}{ky}+{k}^{\mathrm{2}} }=\frac{\mathrm{1}}{{y}^{\mathrm{2}} −\mathrm{2}{ky}−\mathrm{3}{k}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\overset{×} {{y}^{\mathrm{2}} }−\overset{×} {\mathrm{2}{ky}}−\mathrm{3}{k}^{\mathrm{2}} =\overset{×} {{y}^{\mathrm{2}} }−\overset{×} {\mathrm{2}{ky}}+{k}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}{k}^{\mathrm{2}} =\mathrm{0}\Rightarrow{k}=\mathrm{0}\Rightarrow\frac{{a}−{b}}{\mathrm{2}}=\mathrm{0}\Rightarrow{a}={b} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com