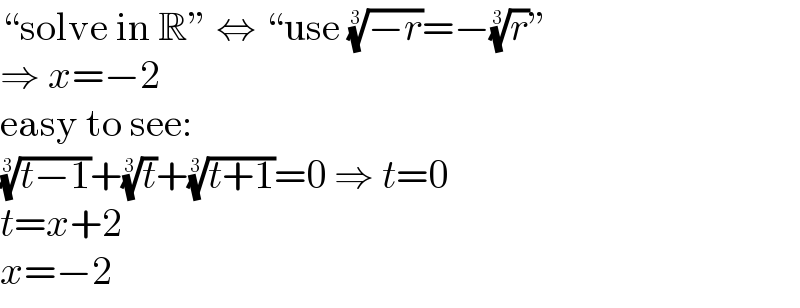Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 181279 by mnjuly1970 last updated on 23/Nov/22

Answered by Rasheed.Sindhi last updated on 25/Nov/22

$$\sqrt[3]{x+1}+\sqrt[3]{x+2}+\sqrt[3]{x+3}=0$$$$\overline{)\begin{array}{c}\underset{\Rightarrow a^3+b^3+c^3-3abc=0}{a+b+c=0}\end{array}}$$$$x+1+x+2+x+3-3\sqrt[3]{(x+1)}\sqrt[3]{x+2}\sqrt[3]{x+3}=0$$$$3(x+2)-3\sqrt[3]{(x+1)}\sqrt[3]{x+2}\sqrt[3]{x+3}=0$$$$3{\left(\sqrt[3]{x+2}\right)}^3-3\sqrt[3]{(x+1)}\sqrt[3]{x+2}\sqrt[3]{x+3}=0$$$$3\left(\sqrt[3]{x+2}\right)({\left(\sqrt[3]{x+2}\right)}^2-\sqrt[3]{(x+1)}\sqrt[3]{x+3})=0$$$$\sqrt[3]{x+2}=0\Rightarrow x+2=0\Rightarrow x=-2$$

Answered by Rasheed.Sindhi last updated on 23/Nov/22

$$\sqrt[3]{x+1}+\sqrt[3]{x+2}+\sqrt[3]{x+3}=0$$$$\sqrt[3]{x+1}+\sqrt[3]{x+2}=-\sqrt[3]{x+3}$$$${(\sqrt[3]{x+1}+\sqrt[3]{x+2})}^3={(-\sqrt[3]{x+3})}^3$$$$(x+1)+(x+2)+3\sqrt[3]{(x+1)(x+2)}(\sqrt[3]{x+1}+\sqrt[3]{x+2})=-x-3$$$$3\sqrt[3]{(x+1)(x+2)}(-\sqrt[3]{x+3})=-3x-6$$$$\sqrt[3]{(x+1)(x+2)}\sqrt[3]{x+3})=x+2$$$$(x+1)(x+2)(x+3)={(x+2)}^3$$$$x^3+6x^2+11x+6=x^3+6x^2+12x+8$$$$11x+6=12x+8$$$$x=-2$$$$$$

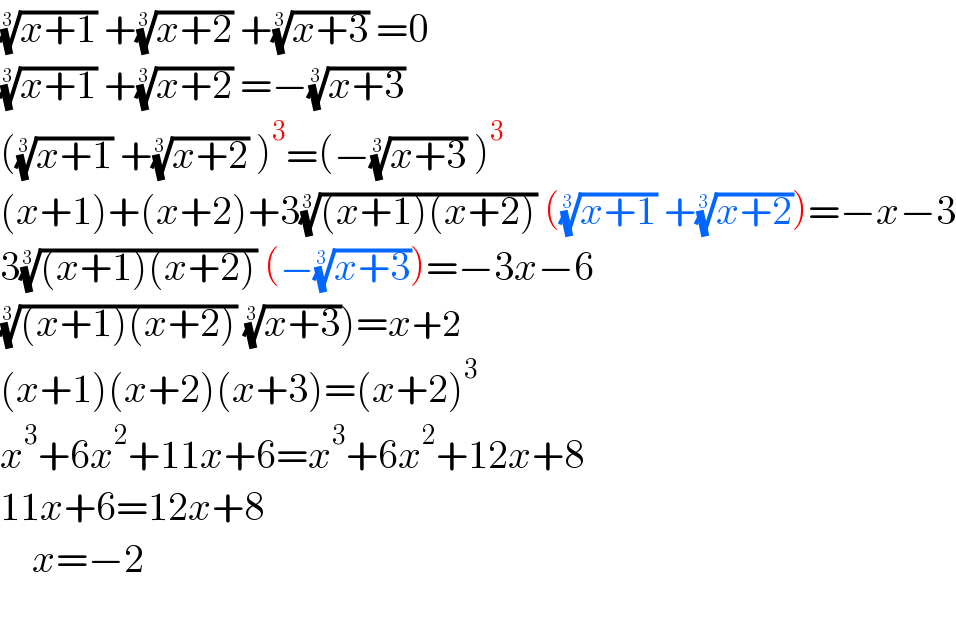
Commented by Frix last updated on 23/Nov/22

$$\mathrm{generally}\mathrm{in}\mathbb{R}:$$$$\sqrt[3]{p}+\sqrt[3]{q}=\sqrt[3]{r}$$$$p+3\sqrt[3]{p^2}\sqrt[3]{q}+3\sqrt[3]{p}\sqrt[3]{q^2}+q=r^3$$$$p+q+3\sqrt[3]{pq}(\sqrt[3]{p}+\sqrt[3]{q})=r^3$$$$p+q+3\sqrt[3]{pq}\sqrt[3]{r}=r^3$$$$3\sqrt[3]{pqr}=r^3-p-q$$$$27pqr={(r^3-p-q)}^3$$$$$$$$\mathrm{from}\mathrm{your}\mathrm{line}$$$$(x+1)(x+2)(x+3)={(x+2)}^3$$$${\mathrm{it}}^{\prime }\mathrm{s}\mathrm{obvious}\mathrm{that}x+2=0\mathrm{is}\mathrm{a}\mathrm{solution}:$$$$(x+1)(x+2)(x+3)-{(x+2)}^3=0$$$$(x+2)((x+1)(x+3)-{(x+2)}^2)=0$$$$\Rightarrow x_1=-2$$

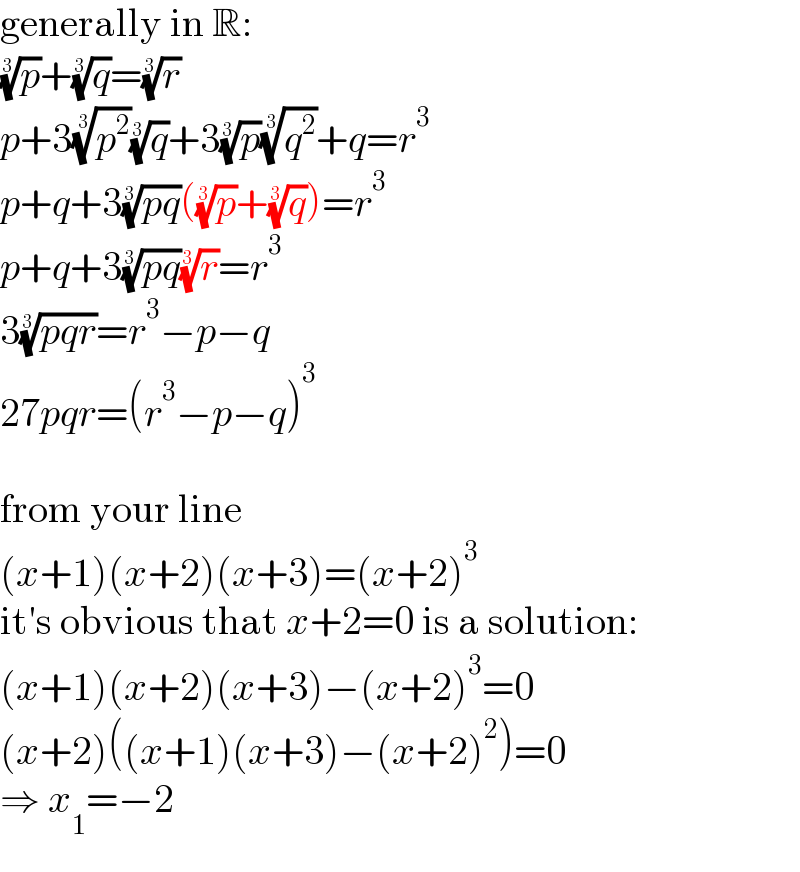
Commented by Rasheed.Sindhi last updated on 23/Nov/22

$$\mathbb{T}\mathrm{hanks}\mathrm{sir}\mathbb{F}\mathrm{r}\stackrel{⧫}{\mathrm{\Pi }}\mathrm{x}!$$

Answered by Frix last updated on 23/Nov/22

$$‘‘\mathrm{solve}\mathrm{in}{\mathbb{R}}^{″}\iff ‘‘\mathrm{use}\sqrt[3]{-r}=-{\sqrt[3]{r}}^{″}$$$$\Rightarrow x=-2$$$$\mathrm{easy}\mathrm{to}\mathrm{see}:$$$$\sqrt[3]{t-1}+\sqrt[3]{t}+\sqrt[3]{t+1}=0\Rightarrow t=0$$$$t=x+2$$$$x=-2$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com