Question Number 181313 by a.lgnaoui last updated on 23/Nov/22
$${Montrer}\:{que} \\ $$$$\mathrm{3}^{\mathrm{2}{n}+\mathrm{1}} +\mathrm{2}^{{n}+\mathrm{2}} \:\:\:{est}\:{divisible}\:{par}\:\mathrm{7} \\ $$
Answered by mr W last updated on 23/Nov/22
$$\mathrm{3}^{\mathrm{2}{n}+\mathrm{1}} +\mathrm{2}^{{n}+\mathrm{2}} \:{mod}\:\mathrm{7} \\ $$$$=\mathrm{3}×\left(\mathrm{7}+\mathrm{2}\right)^{{n}} +\mathrm{4}×\mathrm{2}^{{n}} \:{mod}\:\mathrm{7} \\ $$$$=\mathrm{3}×\mathrm{2}^{{n}} +\mathrm{4}×\mathrm{2}^{{n}} \:{mod}\:\mathrm{7} \\ $$$$=\mathrm{7}×\mathrm{2}^{{n}} \:{mod}\:\mathrm{7} \\ $$$$=\mathrm{0} \\ $$
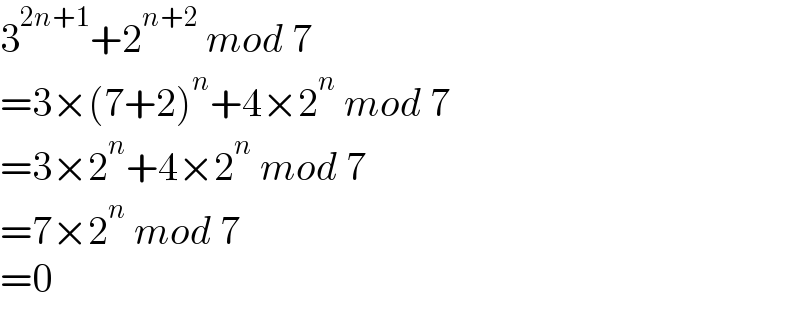
Commented by a.lgnaoui last updated on 24/Nov/22
$${thanks}\: \\ $$
Answered by Acem last updated on 23/Nov/22
![3^( 2n+1) + 2^( n+2) = 3^(2n) ×3 +2^n ×2^2 = 9^( n) ×3 + 2^n ×4 ...(1) 9^1 ≡ 2 [7] ⇒ 9^n ≡ 2^n [7] 3^( 2n+1) + 2^( n+2) ≡ 2^n ×3 +2^n ×4= 2^n ×7 ≡ 0 [7] Donc 3^( 2n+1) + 2^( n+2) est divisible par sept](Q181321.png)
$$\:\mathrm{3}^{\:\mathrm{2}{n}+\mathrm{1}} +\:\mathrm{2}^{\:{n}+\mathrm{2}} \:=\:\mathrm{3}^{\mathrm{2}{n}} ×\mathrm{3}\:+\mathrm{2}^{{n}} ×\mathrm{2}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{9}^{\:{n}} \:×\mathrm{3}\:+\:\mathrm{2}^{{n}} \:×\mathrm{4}\:...\left(\mathrm{1}\right) \\ $$$$\:\mathrm{9}^{\mathrm{1}} \equiv\:\mathrm{2}\:\left[\mathrm{7}\right]\:\Rightarrow\:\mathrm{9}^{{n}} \equiv\:\mathrm{2}^{{n}} \:\left[\mathrm{7}\right]\: \\ $$$$\:\mathrm{3}^{\:\mathrm{2}{n}+\mathrm{1}} +\:\mathrm{2}^{\:{n}+\mathrm{2}} \:\equiv\:\mathrm{2}^{{n}} \:×\mathrm{3}\:+\mathrm{2}^{{n}} ×\mathrm{4}=\:\mathrm{2}^{{n}} ×\mathrm{7} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\equiv\:\mathrm{0}\:\left[\mathrm{7}\right] \\ $$$$ \\ $$$$\:{Donc}\:\:\mathrm{3}^{\:\mathrm{2}{n}+\mathrm{1}} +\:\mathrm{2}^{\:{n}+\mathrm{2}} \:{est}\:{divisible}\:{par}\:{sept} \\ $$$$ \\ $$
Commented by a.lgnaoui last updated on 24/Nov/22
$${thanks} \\ $$
Commented by Acem last updated on 24/Nov/22
$${De}\:{rien} \\ $$