
Question and Answers Forum
Question Number 181323 by KONE last updated on 24/Nov/22

Commented by KONE last updated on 24/Nov/22

Answered by Frix last updated on 24/Nov/22
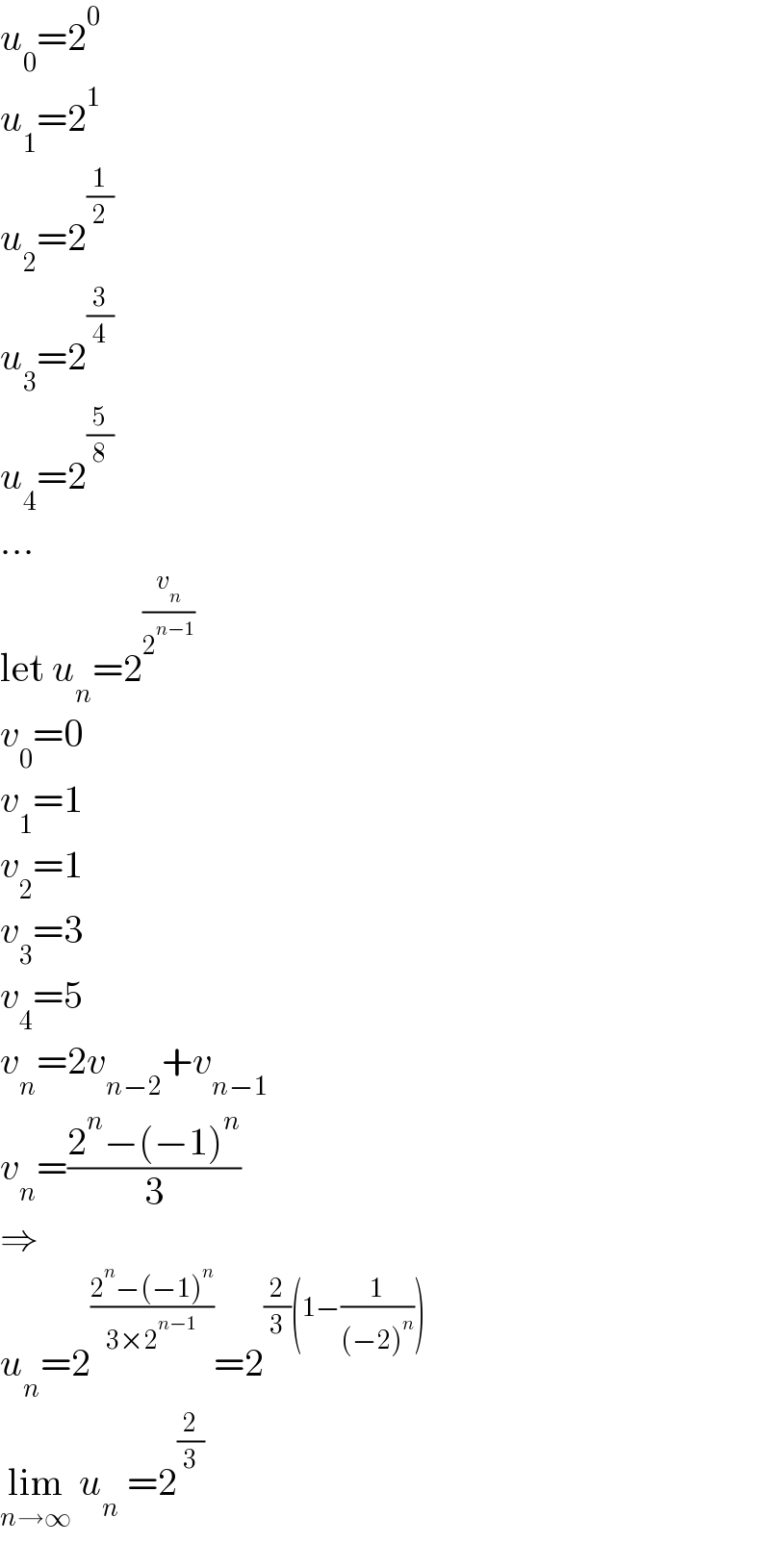
Commented by KONE last updated on 25/Nov/22

Answered by mr W last updated on 24/Nov/22
![U_(n+2) =(√(U_(n+1) U_n )) ln U_(n+2) =(1/2)(ln U_(n+1) +ln U_n ) let a_n =ln U_n 2a_(n+2) −a_(n+1) −a_n =0 let a_n =Cp^n 2Cp^(n+2) −Cp^(n+1) −Cp^n =0 Cp^n (2p^2 −p−1)=0 2p^2 −p−1=0 (2p+1)(p−1)=0 ⇒p=−(1/2) or 1 ⇒a_n =C×(−(1/2))^n +D×(1)^n =(C/((−2)^n ))+D a_0 =ln U_0 =ln 1=0=(C/((−2)^0 ))+D ⇒C+D=0 ...(i) a_1 =ln U_1 =ln 2=(C/((−2)^1 ))+D=−(C/2)+D ⇒−C+2D=2ln 2 ...(ii) ⇒D=((2ln 2)/3) ⇒C=−((2ln 2)/3) ⇒a_n =((2ln 2)/3)(1−(((−1)^n )/2^n ))=ln 2^((2/3)(1−(((−1)^n )/2^n ))) ⇒U_n =e^a_n =2^((2/3)[1−(((−1)^n )/2^n )]) ✓ lim_(n→∞) U_n =2^(2/3) =(4)^(1/3)](Q181351.png)
Commented by mnjuly1970 last updated on 24/Nov/22
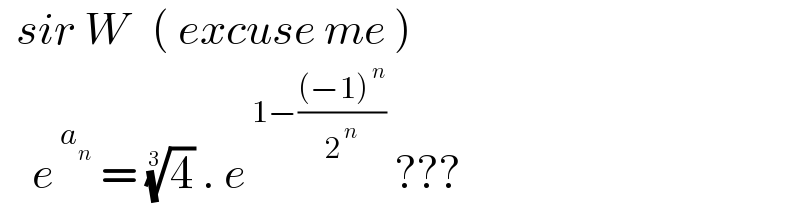
Commented by mnjuly1970 last updated on 24/Nov/22

Commented by mr W last updated on 24/Nov/22

Commented by mnjuly1970 last updated on 24/Nov/22

Commented by KONE last updated on 25/Nov/22

