
Question and Answers Forum
Question Number 181330 by Mastermind last updated on 24/Nov/22
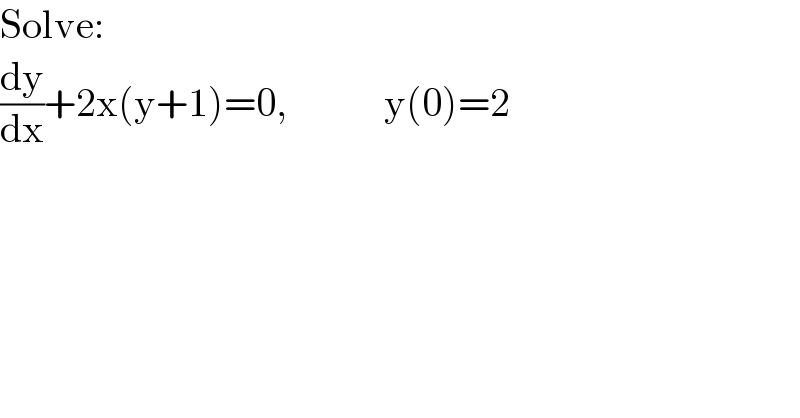
Answered by FelipeLz last updated on 24/Nov/22
![(dy/dx)+2x(y+1) = 0 (dy/dx)+2xy = −2x (dy/dx)e^x^2 +2xe^x^2 y = −2xe^x^2 (d/dx)[ye^x^2 ] = −2xe^x^2 ye^x^2 = −∫2xe^x^2 dx ye^x^2 = −e^x^2 +c y(x) = ce^(−x^2 ) −1 y(0) = 2 → ce^(−0^2 ) −1 = 2 ⇒ c = 3 y(x) = 3e^(−x^2 ) −1 • (dy/dx)+2x(y+1) = 0 (dy/dx) = −2x(y+1) (1/(y+1))dy = −2xdx ∫(1/(y+1))dy = −∫2xdx ln∣y+1∣+c_1 = −x^2 +c_2 ln∣y+1∣ = −x^2 +c_2 −c_1 c_2 −c_1 = c_3 → ln∣y+1∣ = −x^2 +c_3 y+1 = e^(−x^2 +c_3 ) e^c_3 = C → y+1 = Ce^(−x^2 ) y(x) = Ce^(−x^2 ) −1 y(0) = 2 → Ce^(−0^2 ) −1 = 2 ⇒ C = 3 y(x) = 3e^(−x^2 ) −1](Q181353.png)
| ||
Question and Answers Forum | ||
Question Number 181330 by Mastermind last updated on 24/Nov/22 | ||
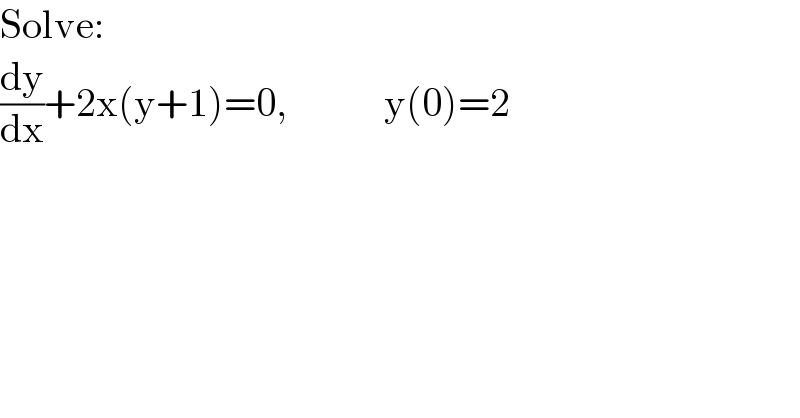 | ||
Answered by FelipeLz last updated on 24/Nov/22 | ||
![(dy/dx)+2x(y+1) = 0 (dy/dx)+2xy = −2x (dy/dx)e^x^2 +2xe^x^2 y = −2xe^x^2 (d/dx)[ye^x^2 ] = −2xe^x^2 ye^x^2 = −∫2xe^x^2 dx ye^x^2 = −e^x^2 +c y(x) = ce^(−x^2 ) −1 y(0) = 2 → ce^(−0^2 ) −1 = 2 ⇒ c = 3 y(x) = 3e^(−x^2 ) −1 • (dy/dx)+2x(y+1) = 0 (dy/dx) = −2x(y+1) (1/(y+1))dy = −2xdx ∫(1/(y+1))dy = −∫2xdx ln∣y+1∣+c_1 = −x^2 +c_2 ln∣y+1∣ = −x^2 +c_2 −c_1 c_2 −c_1 = c_3 → ln∣y+1∣ = −x^2 +c_3 y+1 = e^(−x^2 +c_3 ) e^c_3 = C → y+1 = Ce^(−x^2 ) y(x) = Ce^(−x^2 ) −1 y(0) = 2 → Ce^(−0^2 ) −1 = 2 ⇒ C = 3 y(x) = 3e^(−x^2 ) −1](Q181353.png) | ||
| ||