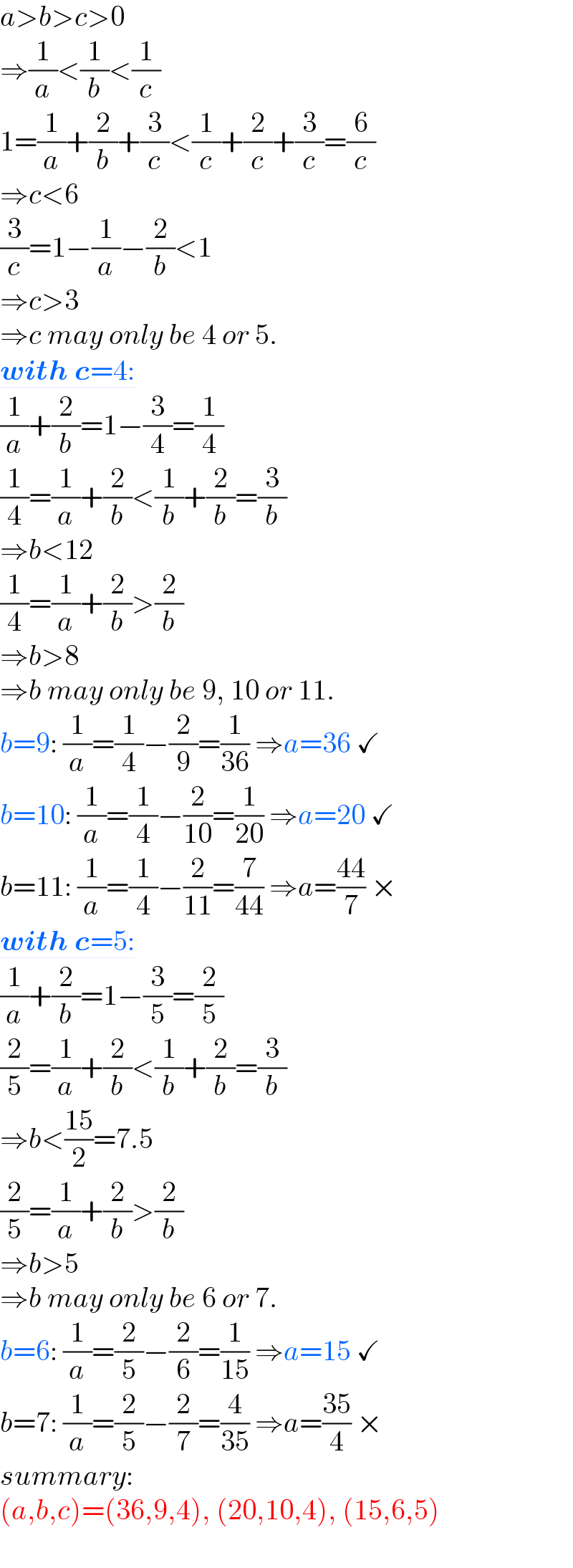find integers a>b>c>0 such that (1/a)+(2/b)+(3/c)=1


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 181837 by mr W last updated on 01/Dec/22

$f i n d i n t e g e r s a > b > c > 0 s u c h t h a t$ $\frac{1}{a} + \frac{2}{b} + \frac{3}{c} = 1$
Commented bySEKRET last updated on 01/Dec/22

$(2; 5; 30) (2; 6; 18) (2; 7; 14) (2; 8; 12)$ $(2; 10; 10) (2; 12; 9) (2; 16; 8) (2; 28; 7)$ $(3; 4; 18) (3; 6; 9) (3; 12; 6) (3; 30; 5)$ $(4; 3; 36) (4; 4; 12) (4; 8; 6) (5; 4; 10)$ $(5; 10; 5) (5; 40; 4) (15; 6; 5) (20; 10; 4)$ $(30; 3; 10) (36; 9; 4) (6; 3; 18) (6; 4; 9)$ $(6; 6; 6) (6; 24; 4) (8; 4; 8) (8; 16; 4) (10; 5; 6)$ $(12; 3; 2) (12; 12; 4) (14; 4; 7) . . . . .$
Commented bymr W last updated on 01/Dec/22

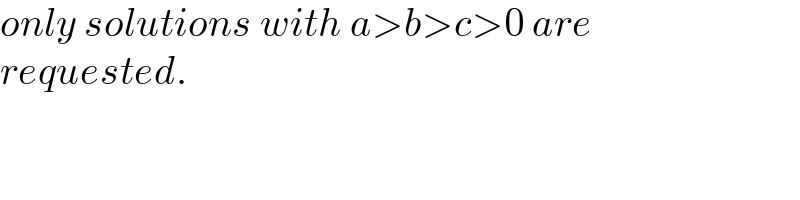
$o n l y s o l u t i o n s w i t h a > b > c > 0 a r e$ $r e q u e s t e d .$
	Answered by prakash jain last updated on 01/Dec/22

	$a = 2$ $b = 8$ $c = 12$
	Commented bymr W last updated on 01/Dec/22

	$t h a n k s f o r t r y i n g s i r!$ $b u t o n l y s o l u t i o n s w i t h a > b > c > 0 a r e$ $r e q u e s t e d .$
	Answered by MJS_new last updated on 01/Dec/22

	$a > b > c > 0 \Rightarrow c > 3$ $a = \frac{b c}{b c - 3 b - 2 c}$ $a > b \Rightarrow \frac{c}{b c - 3 b - 2 c} > 1 \land c > 3$ $\Leftrightarrow$ $c < b < \frac{3 c}{c - 3} \land c > 3 \Rightarrow c = 4 \land 4 < b < 12 \lor c = 5 \land 5 < b < 7.5$ $not many possibilities to try out$ $\Rightarrow$ $a = 36 \land b = 9 \land c = 4$ $a = 20 \land b = 10 \land c = 4$ $a = 15 \land b = 6 \land c = 5$ $are the only solutions$
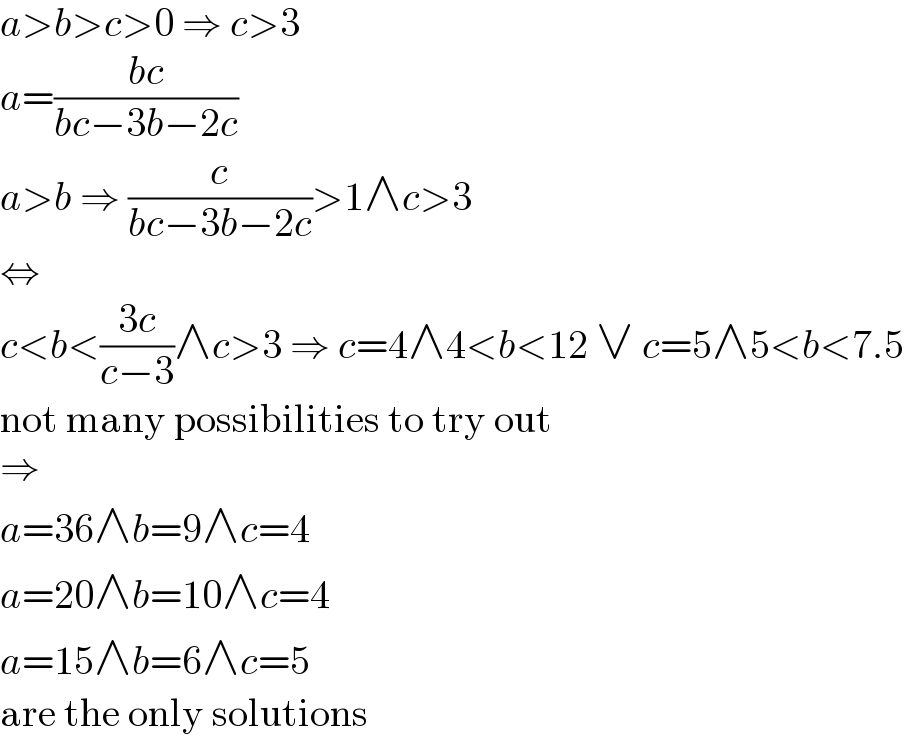
	Commented bymr W last updated on 02/Dec/22

	$t h a n k s a l o t s i r!$
	Answered by mr W last updated on 02/Dec/22

	$a > b > c > 0$ $\Rightarrow \frac{1}{a} < \frac{1}{b} < \frac{1}{c}$ $1 = \frac{1}{a} + \frac{2}{b} + \frac{3}{c} < \frac{1}{c} + \frac{2}{c} + \frac{3}{c} = \frac{6}{c}$ $\Rightarrow c < 6$ $\frac{3}{c} = 1 - \frac{1}{a} - \frac{2}{b} < 1$ $\Rightarrow c > 3$ $\Rightarrow c m a y o n l y b e 4 o r 5 .$ $\underset{―}{w i t h c = 4 :}$ $\frac{1}{a} + \frac{2}{b} = 1 - \frac{3}{4} = \frac{1}{4}$ $\frac{1}{4} = \frac{1}{a} + \frac{2}{b} < \frac{1}{b} + \frac{2}{b} = \frac{3}{b}$ $\Rightarrow b < 12$ $\frac{1}{4} = \frac{1}{a} + \frac{2}{b} > \frac{2}{b}$ $\Rightarrow b > 8$ $\Rightarrow b m a y o n l y b e 9, 10 o r 11 .$ $b = 9 : \frac{1}{a} = \frac{1}{4} - \frac{2}{9} = \frac{1}{36} \Rightarrow a = 36 ✓$ $b = 10 : \frac{1}{a} = \frac{1}{4} - \frac{2}{10} = \frac{1}{20} \Rightarrow a = 20 ✓$ $b = 11 : \frac{1}{a} = \frac{1}{4} - \frac{2}{11} = \frac{7}{44} \Rightarrow a = \frac{44}{7} \times$ $\underset{―}{w i t h c = 5 :}$ $\frac{1}{a} + \frac{2}{b} = 1 - \frac{3}{5} = \frac{2}{5}$ $\frac{2}{5} = \frac{1}{a} + \frac{2}{b} < \frac{1}{b} + \frac{2}{b} = \frac{3}{b}$ $\Rightarrow b < \frac{15}{2} = 7.5$ $\frac{2}{5} = \frac{1}{a} + \frac{2}{b} > \frac{2}{b}$ $\Rightarrow b > 5$ $\Rightarrow b m a y o n l y b e 6 o r 7 .$ $b = 6 : \frac{1}{a} = \frac{2}{5} - \frac{2}{6} = \frac{1}{15} \Rightarrow a = 15 ✓$ $b = 7 : \frac{1}{a} = \frac{2}{5} - \frac{2}{7} = \frac{4}{35} \Rightarrow a = \frac{35}{4} \times$ $s u m m a r y :$ $(a, b, c) = (36, 9, 4), (20, 10, 4), (15, 6, 5)$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum