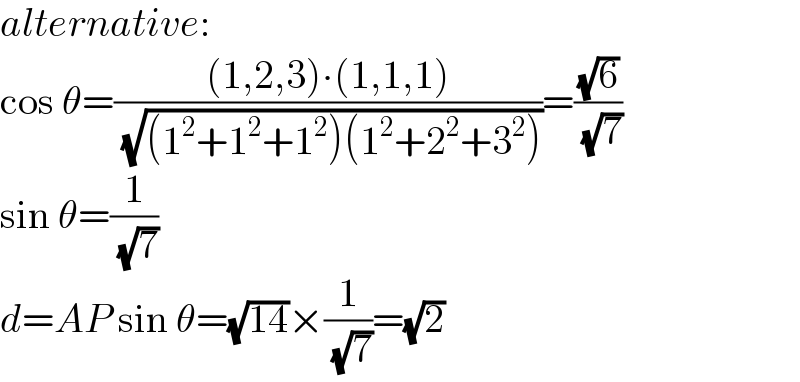Question and Answers Forum
Question Number 181875 by mr W last updated on 01/Dec/22

Commented by mr W last updated on 01/Dec/22
Commented by SEKRET last updated on 01/Dec/22

Commented by mr W last updated on 01/Dec/22
Answered by SEKRET last updated on 01/Dec/22

Commented by mr W last updated on 01/Dec/22
Answered by SEKRET last updated on 01/Dec/22
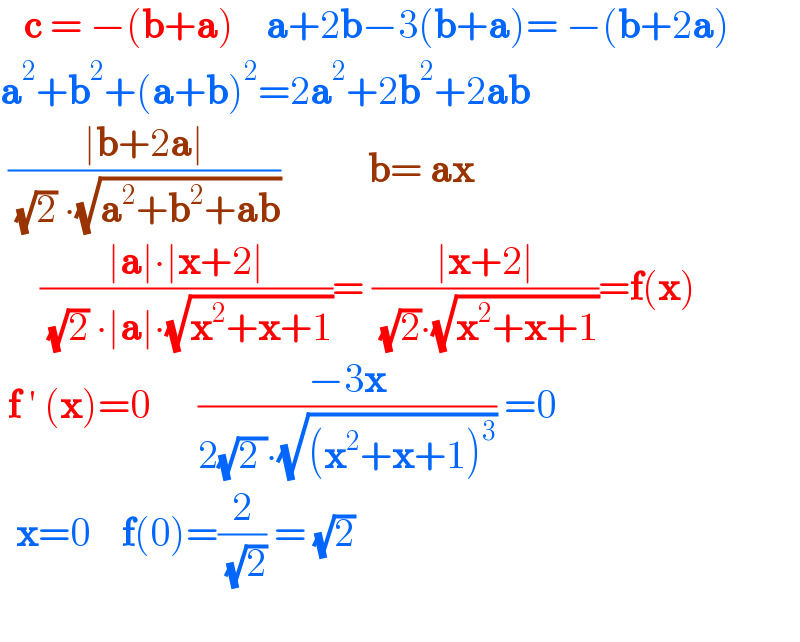
Commented by mr W last updated on 01/Dec/22

Answered by mr W last updated on 02/Dec/22
![I) regular method b=−(a+c) f=((∣a+2b+3c∣)/( (√(a^2 +b^2 +c^2 )))) =((∣a−2a−2c+3c∣)/( (√(a^2 +(a+c)^2 +c^2 )))) =((∣c−a∣)/( (√(2(a^2 +ac+c^2 ))))) =((∣k−1∣)/( (√(2(1+k+k^2 ))))) with k=(c/a) =((∣k−1∣)/( (√(2((k−1)^2 +3(k−1)+3))))) =((∣u∣)/( (√(2(u^2 +3u+3))))) with u=k−1 =(1/( (√(2((3/u^2 )+(3/u)+1))))) =(1/( (√(6[((1/u)+(1/2))^2 +(1/(12))])))) ≤(1/( (√(6×(1/(12))))))=(√2) ⇒maximum =(√2) at u=−2=k−1=(c/a)−1 ⇒c+a=0, b=0](Q181892.png)
Commented by SEKRET last updated on 01/Dec/22

Answered by mr W last updated on 02/Dec/22

Commented by mr W last updated on 01/Dec/22
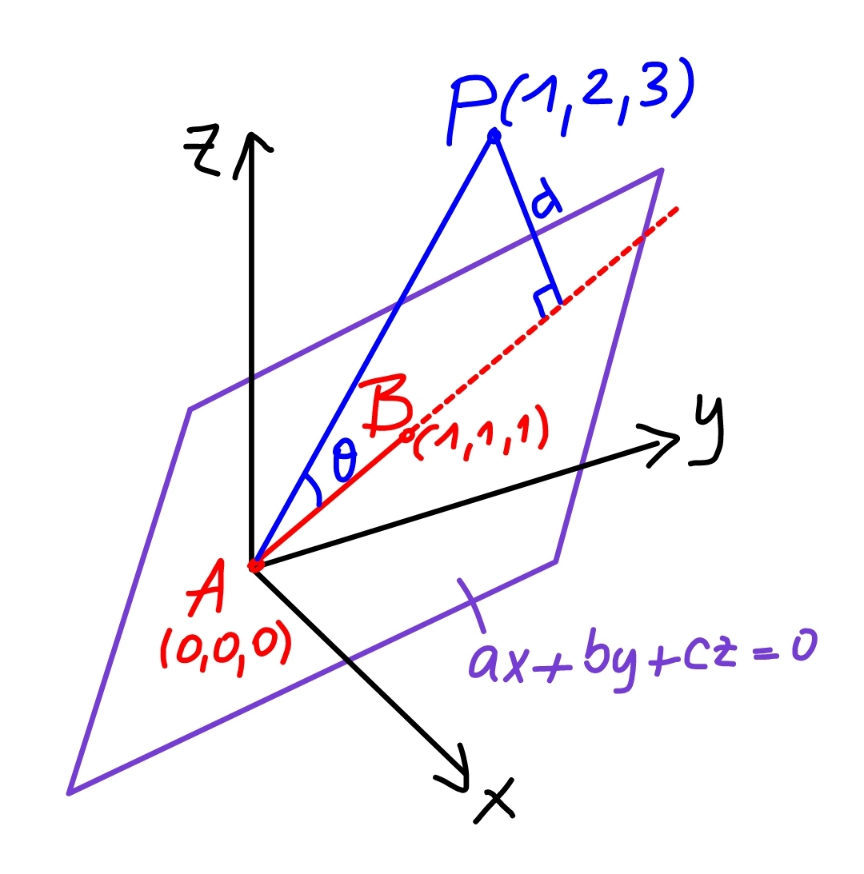
Commented by mr W last updated on 02/Dec/22