
Question and Answers Forum
Question Number 181897 by Acem last updated on 01/Dec/22

Answered by mr W last updated on 02/Dec/22
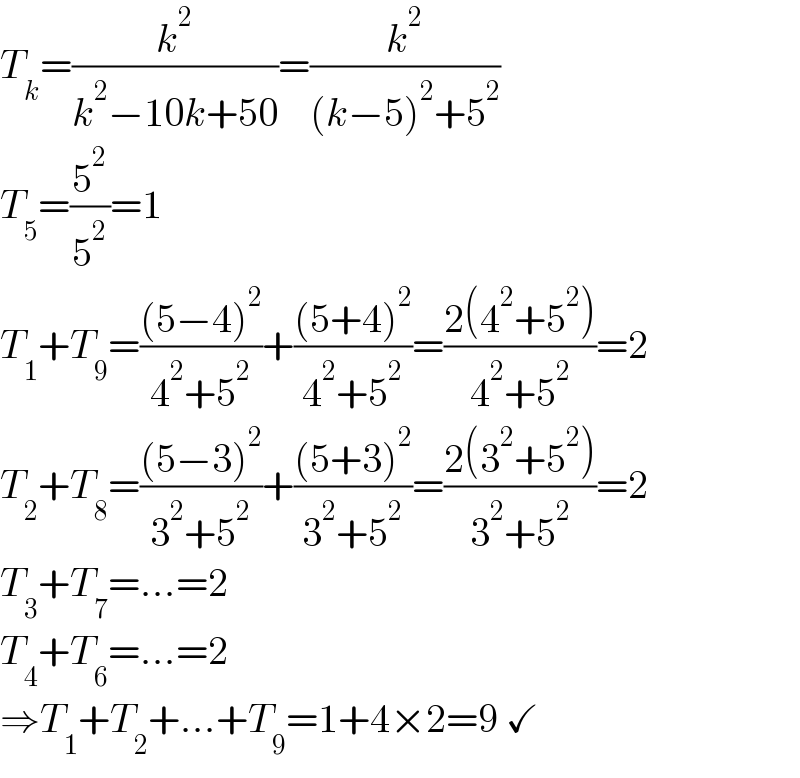
Commented by Acem last updated on 02/Dec/22

Answered by Acem last updated on 02/Dec/22
![(1^2 /(1^2 −10+50))= ((2.1^2 )/(1^2 +1−20+100))= ((2.1^2 )/(1^2 + (10−1)^2 )) ...i (9^2 /(9^2 −90+50))= ((2 (10−1)^2 )/((10−1)^2 +(10−1)^2 −20(10−1)+100)) = ((2 (10−1)^2 )/((10−1)^2 +[10−(10−1)]^2 ))= ((2 (10−1)^2 )/(1^2 +(10−1)^2 )) ...ii i+ii = ((2 [1+(10−1)^2 ])/(1+(10−1)^2 ))= 2 Then ((2n^2 )/(n^2 +(10−n)^2 ))+ ((2 (10−n)^2 )/(n^2 +(10−n)^2 ))= 2 ∀n∈ N, n> 0 we have n= 9 : n=1 to 9 ; Terms= {1, 2, ..., 9} Sum= 4×2_(1,9& 2,8,...) + T_5 = 9 ; T_5 = 1](Q181941.png)
| ||
Question and Answers Forum | ||
Question Number 181897 by Acem last updated on 01/Dec/22 | ||
 | ||
Answered by mr W last updated on 02/Dec/22 | ||
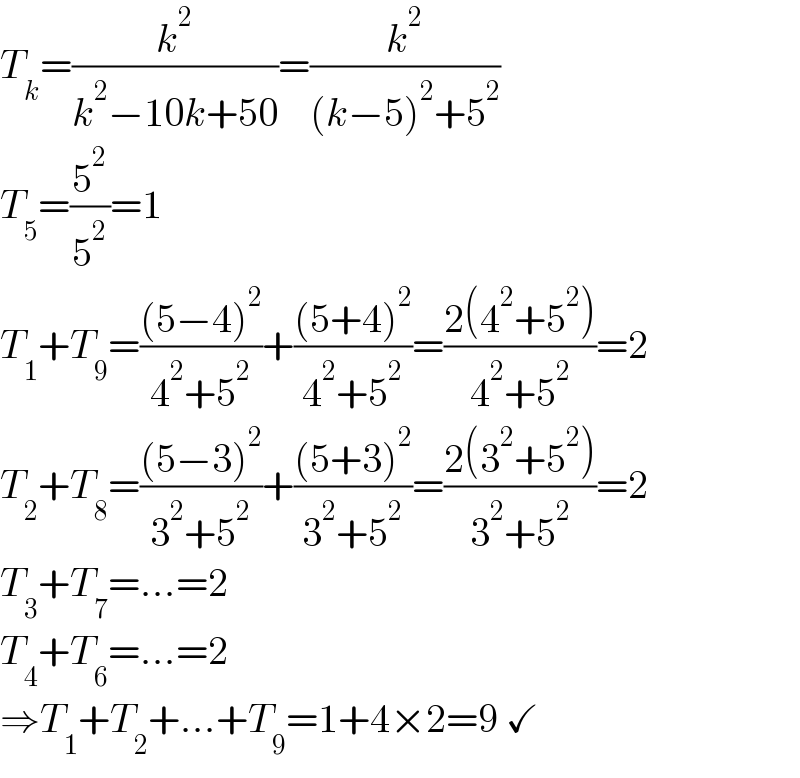 | ||
| ||
Commented by Acem last updated on 02/Dec/22 | ||
 | ||
Answered by Acem last updated on 02/Dec/22 | ||
![(1^2 /(1^2 −10+50))= ((2.1^2 )/(1^2 +1−20+100))= ((2.1^2 )/(1^2 + (10−1)^2 )) ...i (9^2 /(9^2 −90+50))= ((2 (10−1)^2 )/((10−1)^2 +(10−1)^2 −20(10−1)+100)) = ((2 (10−1)^2 )/((10−1)^2 +[10−(10−1)]^2 ))= ((2 (10−1)^2 )/(1^2 +(10−1)^2 )) ...ii i+ii = ((2 [1+(10−1)^2 ])/(1+(10−1)^2 ))= 2 Then ((2n^2 )/(n^2 +(10−n)^2 ))+ ((2 (10−n)^2 )/(n^2 +(10−n)^2 ))= 2 ∀n∈ N, n> 0 we have n= 9 : n=1 to 9 ; Terms= {1, 2, ..., 9} Sum= 4×2_(1,9& 2,8,...) + T_5 = 9 ; T_5 = 1](Q181941.png) | ||
| ||