Math Question and Answers


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 181902 by Acem last updated on 01/Dec/22

	Answered by Rasheed.Sindhi last updated on 02/Dec/22
	$(x^2 +xy+y^2 )(√(x^2 +y^2 )) =185....(i) (x^2 −xy+y^2 )(√(x^2 +y^2 )) =65.....(ii) [(√(x^2 +y^2 )) ≠0] (i)/(ii): ((x^2 +xy+y^2 )/(x^2 −xy+y^2 ))=((185)/(65))=((37)/(13)) ((x^2 +xy+y^2 −x^2 +xy−y^2 )/(x^2 +xy+y^2 +x^2 −xy+y^2 ))=((37−13)/(37+13)) [Componendo-Dividendo property] ((2xy)/(2x^2 +2y^2 ))=((37−13)/(37+13)) ((xy)/(x^2 +y^2 ))=((12)/(25)) 12x^2 −25xy+12y^2 =0 ((12x)/(25y))+((12y)/(25x))=1 ((12)/(25))(t+(1/t))=1 t+(1/t)=((25)/(12)) 12t^2 −25t+12=0 t=((25±(√(625−576)))/(24))=((25±7)/(24))=(4/3),(3/4) (x/y)=(4/3),(3/4) 3x=4y ∨ 4x=3y y=((3x)/4),((4x)/3) y=((3x)/4): (i)⇒( x^2 +x(((3x)/4))+(((3x)/4))^2 )(√(x^2 +(((3x)/4))^2 )) =185 ((16x^2 +12x^2 +9x^2 )/(16))(√((16x^2 +9x^2 )/(16))) =185 ((37x^2 )/(16))∙((5∣x∣)/4) =185 ∣x∣^3 =((185∙64)/(5∙37))=4^3 ⇒∣x∣=4⇒x=±4 ⇒y=((3(±4))/4)=±3 y=((4x)/3): (i)⇒(x^2 +x(((4x)/3))+(((4x)/3))^2 )(√(x^2 +(((4x)/3))^2 )) =185 ((9x^2 +12x^2 +16x^2 )/9)(√((9x^2 +16x^2 )/9)) =185 ((37x^2 )/9)∙((5∣x∣)/3)=185 ∣x∣^3 =((185×27)/(37×5))⇒∣x∣=3⇒x=±3 ⇒y=((4(±3))/3)=±4 (x,y)={(4,3),(3,4),(−4,−3),(−3,−4)}$
	$(x^{2} + x y + y^{2}) \sqrt{x^{2} + y^{2}} = 185 . . . . (i)$ $(x^{2} - x y + y^{2}) \sqrt{x^{2} + y^{2}} = 65 . . . . . (i i)$ $[\sqrt{x^{2} + y^{2}} \neq 0]$ $(i) / (i i) : \frac{x^{2} + x y + y^{2}}{x^{2} - x y + y^{2}} = \frac{185}{65} = \frac{37}{13}$ $\frac{x^{2} + x y + y^{2} - x^{2} + x y - y^{2}}{x^{2} + x y + y^{2} + x^{2} - x y + y^{2}} = \frac{37 - 13}{37 + 13}$ $[C o m p o n e n d o - D i v i d e n d o p r o p e r t y]$ $\frac{2 x y}{2 x^{2} + 2 y^{2}} = \frac{37 - 13}{37 + 13}$ $\frac{x y}{x^{2} + y^{2}} = \frac{12}{25}$ $12 x^{2} - 25 x y + 12 y^{2} = 0$ $\frac{12 x}{25 y} + \frac{12 y}{25 x} = 1$ $\frac{12}{25} (t + \frac{1}{t}) = 1$ $t + \frac{1}{t} = \frac{25}{12}$ $12 t^{2} - 25 t + 12 = 0$ $t = \frac{25 \pm \sqrt{625 - 576}}{24} = \frac{25 \pm 7}{24} = \frac{4}{3}, \frac{3}{4}$ $\frac{x}{y} = \frac{4}{3}, \frac{3}{4}$ $3 x = 4 y \lor 4 x = 3 y$ $y = \frac{3 x}{4}, \frac{4 x}{3}$ $y = \frac{3 x}{4} :$ $(i) \Rightarrow (x^{2} + x (\frac{3 x}{4}) + {(\frac{3 x}{4})}^{2}) \sqrt{x^{2} + {(\frac{3 x}{4})}^{2}} = 185$ $\frac{16 x^{2} + 12 x^{2} + 9 x^{2}}{16} \sqrt{\frac{16 x^{2} + 9 x^{2}}{16}} = 185$ $\frac{37 x^{2}}{16} \cdot \frac{5 ∣ x ∣}{4} = 185$ $∣ x ∣^{3} = \frac{185 \cdot 64}{5 \cdot 37} = 4^{3} \Rightarrow∣ x ∣= 4 \Rightarrow x = \pm 4$ $\Rightarrow y = \frac{3 (\pm 4)}{4} = \pm 3$ $y = \frac{4 x}{3} :$ $(i) \Rightarrow (x^{2} + x (\frac{4 x}{3}) + {(\frac{4 x}{3})}^{2}) \sqrt{x^{2} + {(\frac{4 x}{3})}^{2}} = 185$ $\frac{9 x^{2} + 12 x^{2} + 16 x^{2}}{9} \sqrt{\frac{9 x^{2} + 16 x^{2}}{9}} = 185$ $\frac{37 x^{2}}{9} \cdot \frac{5 ∣ x ∣}{3} = 185$ $∣ x ∣^{3} = \frac{185 \times 27}{37 \times 5} \Rightarrow∣ x ∣= 3 \Rightarrow x = \pm 3$ $\Rightarrow y = \frac{4 (\pm 3)}{3} = \pm 4$ $(x, y) = {(4, 3), (3, 4), (- 4, - 3), (- 3, - 4)}$
	Answered by mr W last updated on 02/Dec/22

	$u = \sqrt{x^{2} + y^{2}}$ $v = x y$ $(u^{2} + v) u = 185 . . . (i)$ $(u^{2} - v) u = 65 . . . (i i)$ $2 u^{3} = 185 + 65 = 250$ $\Rightarrow u = 5 = \sqrt{x^{2} + y^{2}}$ $\Rightarrow v = \frac{185}{5} - 5^{2} = 12 = x y$ $x^{2} + y^{2} = 25 \Rightarrow {(x + y)}^{2} = 25 + 2 \times 12 = 49$ $\Rightarrow x + y = \pm 7$ $\Rightarrow (x, y) = (3, 4) o r (4, 3) o r (- 3, - 4) o r (- 4, - 3)$
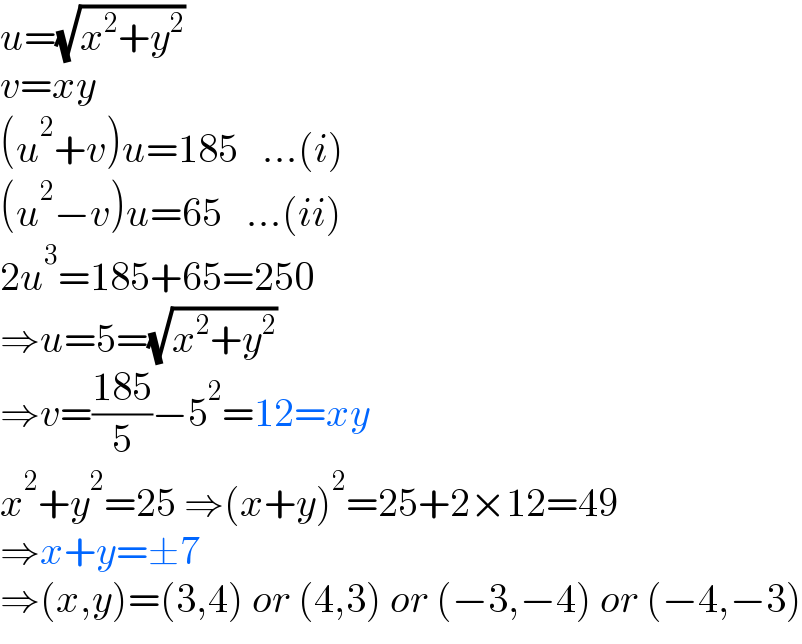
	Commented by Acem last updated on 02/Dec/22

	$N e a t S o l u t i o n!$
	Answered by Rasheed.Sindhi last updated on 02/Dec/22
	$(x^2 +xy+y^2 )(√(x^2 +y^2 )) =185....(i) (x^2 −xy+y^2 )(√(x^2 +y^2 )) =65....(ii) [(√(x^2 +y^2 )) ≠0] (i)×13 & (ii)×37 13(x^2 +xy+y^2 )(√(x^2 +y^2 )) =2405...(iii) 37(x^2 −xy+y^2 )(√(x^2 +y^2 )) =2405...(iv) (iii)&(iv): 13(x^2 +xy+y^2 )=37(x^2 −xy+y^2 ) 12x^2 −25xy+12y^2 =0 ((12x^2 )/(25xy))−1+((12y^2 )/(25xy))=0 ((12)/(25))((x/y)+(y/x))=1 t+(1/t)=((25)/(12)) 12t^2 −25t+12=0 t=((25±(√(625−576)))/(24))=((25±7)/(24))=(4/3),(3/4) (x/y)=(4/3),(3/4) 3x=4y ∨ 4x=3y y= ((3x)/4),((4x)/3) y=((3x)/4): (i)⇒(x^2 +x(((3x)/4))+(((3x)/4))^2 )(√(x^2 +(((3x)/4))^2 )) =185 ((16x^2 +12x^2 +9x^2 )/(16))(√((16x^2 +9x^2 )/(16))) =185 ((37x^2 )/(16))∙((5∣x∣)/4)=185 ∣x∣^3 =64 x=±4⇒y=((3(±4))/4)=±3 y= ((4x)/3): (i)⇒(x^2 +x(((4x)/3))+(((4x)/3))^2 )(√(x^2 +(((4x)/3))^2 )) =185 ((9x^2 +12x^2 +16x^2 )/9)(√((9x^2 +16x^2 )/9)) =185 ((37x^2 )/9)∙((5∣x∣)/3)=185 ∣x∣^3 =27⇒x=±3 ⇒y=((4(±3))/3)=±4 (x,y)={(3,4),(4,3),(−3,−4),(−4,−3)}$
	$(x^{2} + x y + y^{2}) \sqrt{x^{2} + y^{2}} = 185 . . . . (i)$ $(x^{2} - x y + y^{2}) \sqrt{x^{2} + y^{2}} = 65 . . . . (i i)$ $[\sqrt{x^{2} + y^{2}} \neq 0]$ $(i) \times 13 & (i i) \times 37$ $13 (x^{2} + x y + y^{2}) \sqrt{x^{2} + y^{2}} = 2405 . . . (i i i)$ $37 (x^{2} - x y + y^{2}) \sqrt{x^{2} + y^{2}} = 2405 . . . (i v)$ $(i i i) & (i v) :$ $13 (x^{2} + x y + y^{2}) = 37 (x^{2} - x y + y^{2})$ $12 x^{2} - 25 x y + 12 y^{2} = 0$ $\frac{12 x^{2}}{25 x y} - 1 + \frac{12 y^{2}}{25 x y} = 0$ $\frac{12}{25} (\frac{x}{y} + \frac{y}{x}) = 1$ $t + \frac{1}{t} = \frac{25}{12}$ $12 t^{2} - 25 t + 12 = 0$ $t = \frac{25 \pm \sqrt{625 - 576}}{24} = \frac{25 \pm 7}{24} = \frac{4}{3}, \frac{3}{4}$ $\frac{x}{y} = \frac{4}{3}, \frac{3}{4}$ $3 x = 4 y \lor 4 x = 3 y$ $y = \frac{3 x}{4}, \frac{4 x}{3}$ $y = \frac{3 x}{4} :$ $(i) \Rightarrow (x^{2} + x (\frac{3 x}{4}) + {(\frac{3 x}{4})}^{2}) \sqrt{x^{2} + {(\frac{3 x}{4})}^{2}} = 185$ $\frac{16 x^{2} + 12 x^{2} + 9 x^{2}}{16} \sqrt{\frac{16 x^{2} + 9 x^{2}}{16}} = 185$ $\frac{37 x^{2}}{16} \cdot \frac{5 ∣ x ∣}{4} = 185$ $∣ x ∣^{3} = 64$ $x = \pm 4 \Rightarrow y = \frac{3 (\pm 4)}{4} = \pm 3$ $y = \frac{4 x}{3} :$ $(i) \Rightarrow (x^{2} + x (\frac{4 x}{3}) + {(\frac{4 x}{3})}^{2}) \sqrt{x^{2} + {(\frac{4 x}{3})}^{2}} = 185$ $\frac{9 x^{2} + 12 x^{2} + 16 x^{2}}{9} \sqrt{\frac{9 x^{2} + 16 x^{2}}{9}} = 185$ $\frac{37 x^{2}}{9} \cdot \frac{5 ∣ x ∣}{3} = 185$ $∣ x ∣^{3} = 27 \Rightarrow x = \pm 3$ $\Rightarrow y = \frac{4 (\pm 3)}{3} = \pm 4$ $(x, y) = {(3, 4), (4, 3), (- 3, - 4), (- 4, - 3)}$
	Commented by Acem last updated on 02/Dec/22
	$Mr. Rasheed thank you for your efforts! Anyway, if you didn′t assume new variable, you can solve it directly without multiply the formulas by 13, 37 As you see if we sum i, ii we will save a lot of work (x^2 +y^2 ) (√(x^2 +y^2 ))= 125 ⇒ x^2 +y^2 = 25 ... iii iii ∧ ii: 25−xy= 13 ⇒ xy= 12 ... iv Now, (x+y)^2 = x^2 +y^2 + 2xy= 49 ⇒ x+y= ±7 ... v iv ∧ v: ∴ { ((x+y= 7)),(( xy= 12)) :} or { ((x+y= −7)),(( xy= 12)) :} ⇒ S={(4,3), (3,4), (−4, −3), (−3,−4)}$
	$M r . R a s h e e d t h a n k y o u f o r y o u r e f f o r t s!$ $A n y w a y, i f y o u {d i d n}^{'} t a s s u m e n e w v a r i a b l e, y o u$ $c a n s o l v e i t d i r e c t l y w i t h o u t m u l t i p l y t h e$ $f o r m u l a s b y 13, 37$ $A s y o u s e e i f w e s u m i, i i w e w i l l s a v e a l o t o f w o r k$ $(x^{2} + y^{2}) \sqrt{x^{2} + y^{2}} = 125 \Rightarrow x^{2} + y^{2} = 25 . . . i i i$ $i i i \land i i : 25 - x y = 13 \Rightarrow x y = 12 . . . i v$ $N o w, {(x + y)}^{2} = x^{2} + y^{2} + 2 x y = 49$ $\Rightarrow x + y = \pm 7 . . . v$ $i v \land v :$ $∴ {\begin{cases} x + y = 7 \\ x y = 12 \end{cases} o r {\begin{cases} x + y = - 7 \\ x y = 12 \end{cases}$ $\Rightarrow S = {(4, 3), (3, 4), (- 4, - 3), (- 3, - 4)}$
	Commented by Rasheed.Sindhi last updated on 02/Dec/22

	$A g r e e s i r, {t h a t}^{'} s m o r e e f f i c i e n t w a y!$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum