
Question and Answers Forum
Question Number 182006 by mr W last updated on 03/Dec/22
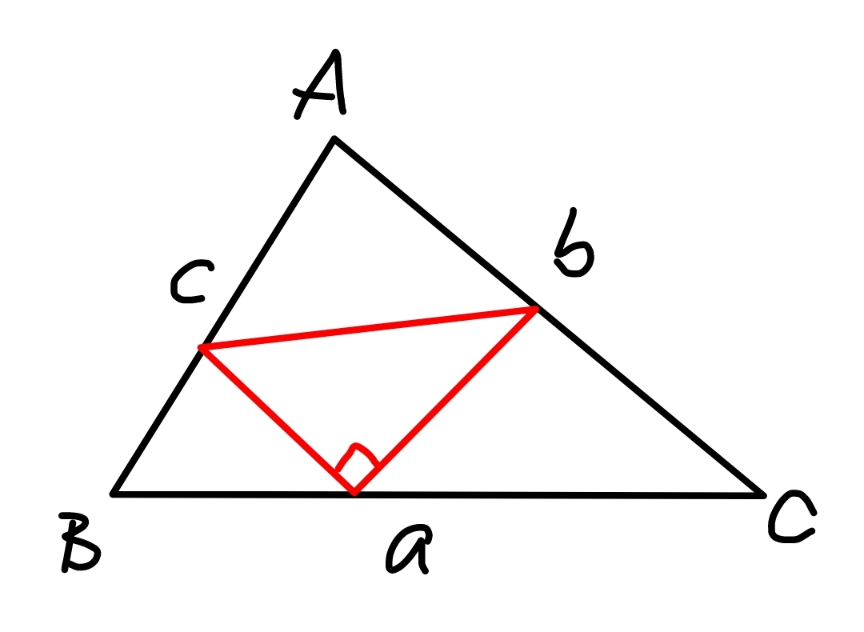
Commented by mr W last updated on 03/Dec/22
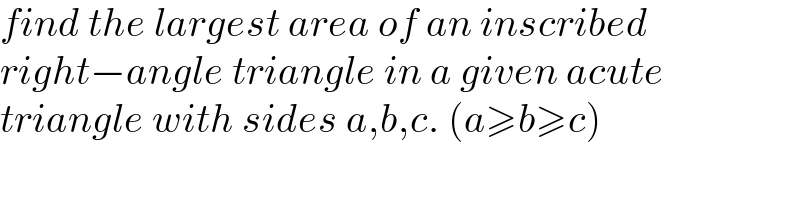
Commented by Acem last updated on 03/Dec/22

Answered by mr W last updated on 03/Dec/22
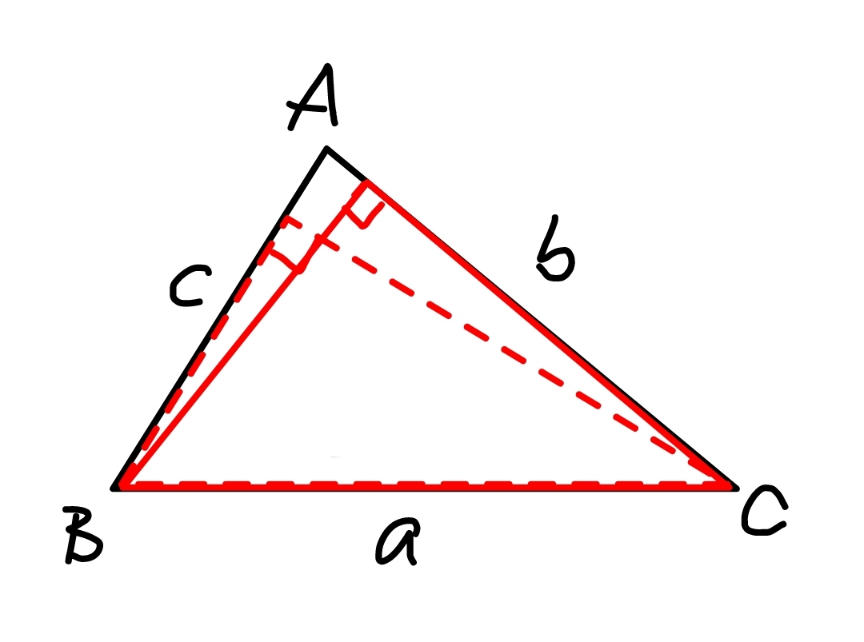
Commented by mr W last updated on 03/Dec/22
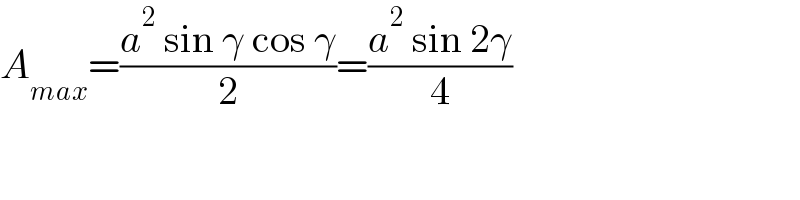
Commented by Acem last updated on 03/Dec/22
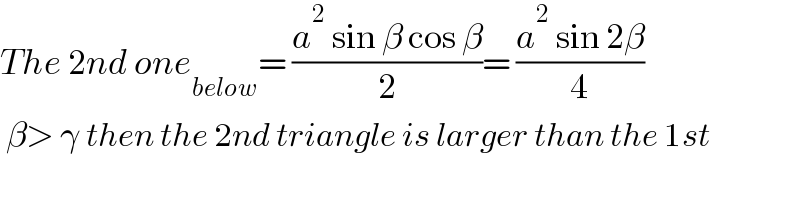
Commented by mr W last updated on 03/Dec/22
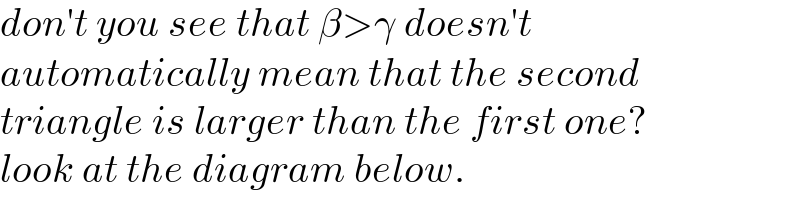
Commented by mr W last updated on 03/Dec/22
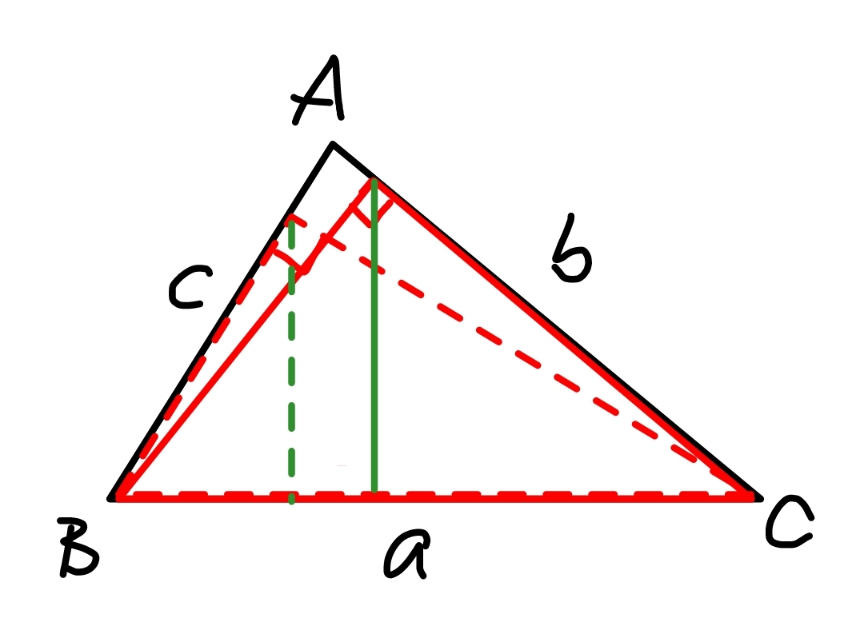
Commented by mr W last updated on 03/Dec/22
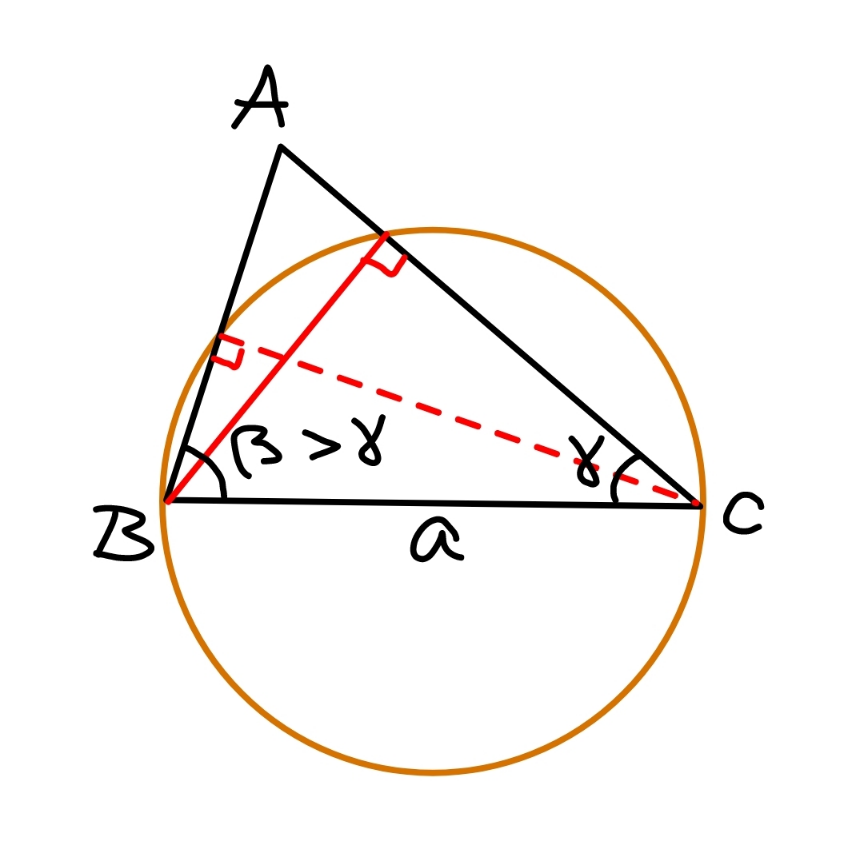
Commented by mr W last updated on 03/Dec/22
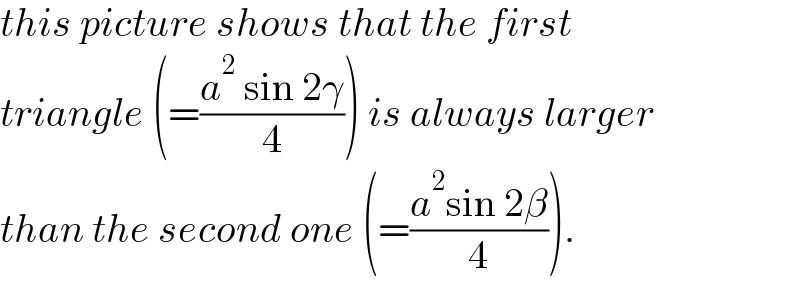
Commented by Acem last updated on 03/Dec/22
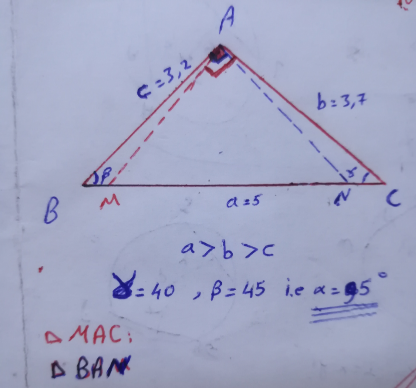
Commented by Acem last updated on 03/Dec/22

Commented by Acem last updated on 04/Dec/22
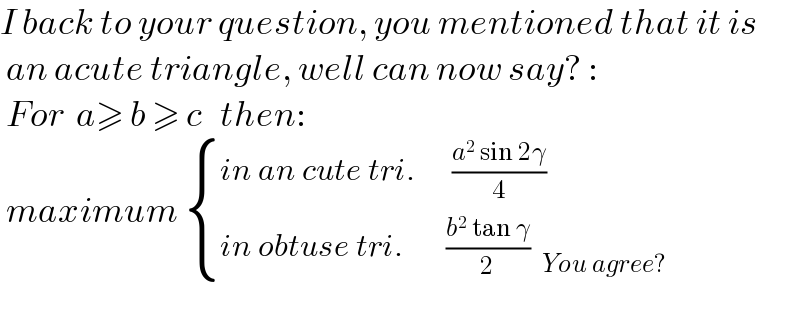
Commented by mr W last updated on 04/Dec/22

