
Question and Answers Forum
Question Number 182045 by Emrice last updated on 03/Dec/22
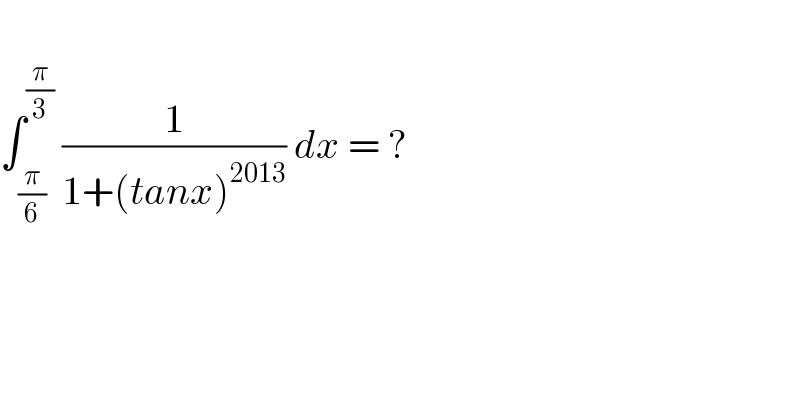
Commented by Frix last updated on 03/Dec/22
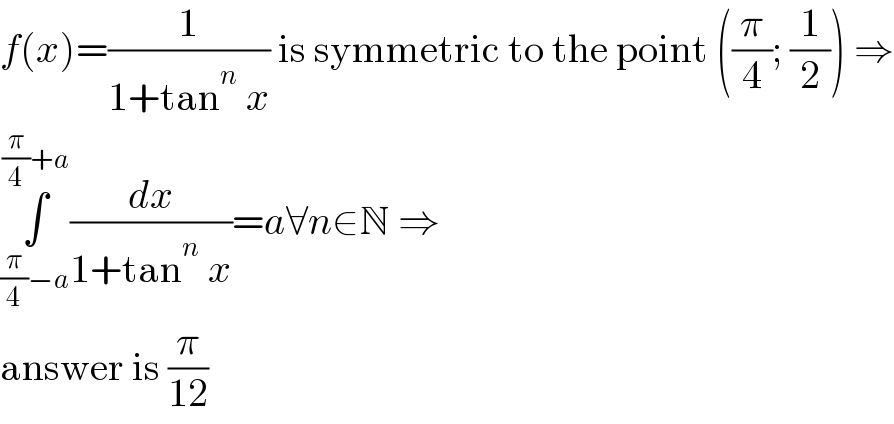
Answered by Ar Brandon last updated on 03/Dec/22
![I=∫_(π/6) ^(π/3) (1/(1+(tanx)^(2013) ))dx I=∫_(π/6) ^(π/3) (((cosx)^(2013) )/((cosx)^(2013) +(sinx)^(2013) ))dx ...eqn(i) I=∫_(π/6) ^(π/3) (((sinx)^(2013) )/((cosx)^(2013) +(sinx)^(2013) ))dx ...eqn(ii) eqn(i)+eqn(ii) 2I=∫_(π/6) ^(π/3) (((cosx)^(2013) +(sinx)^(2013) )/((cosx)^(2013) +(sinx)^(2013) ))dx=∫_(π/6) ^(π/3) dx ⇒I=(1/2)[x]_(π/6) ^(π/3) =(1/2)((π/3)−(π/6))=(1/2)((π/6))= determinant (((π/(12))))](Q182061.png)
Answered by SEKRET last updated on 04/Dec/22
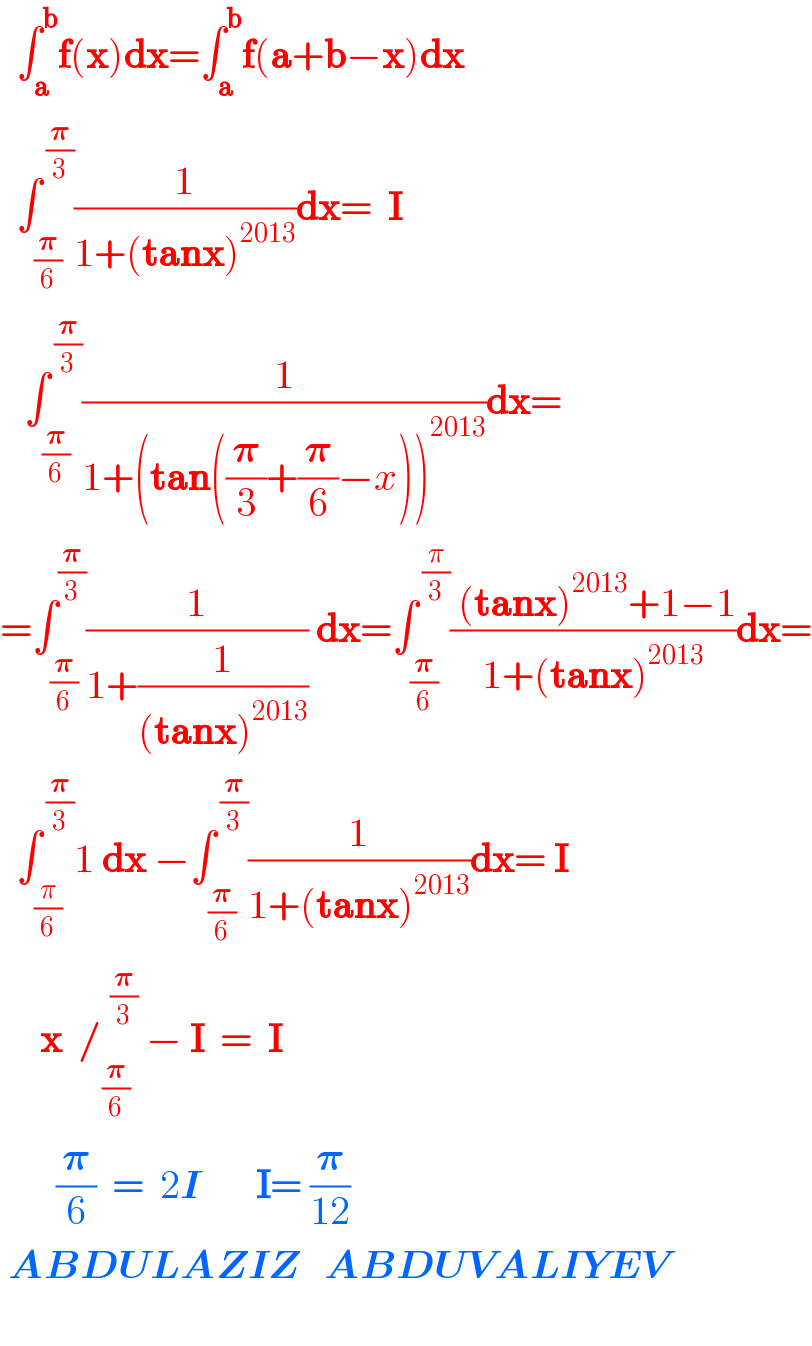
| ||
Question and Answers Forum | ||
Question Number 182045 by Emrice last updated on 03/Dec/22 | ||
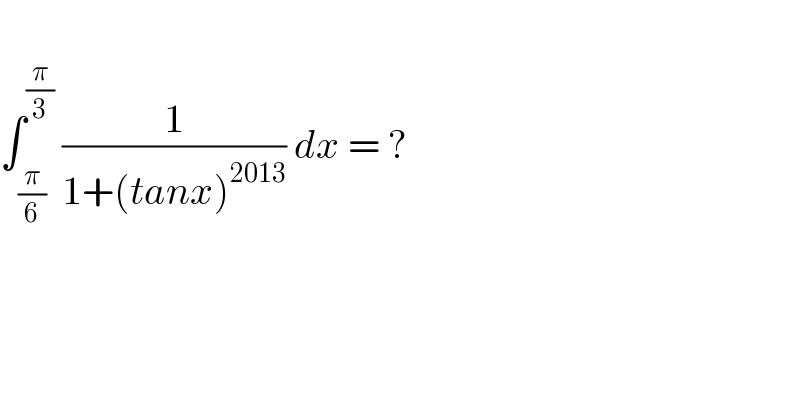 | ||
Commented by Frix last updated on 03/Dec/22 | ||
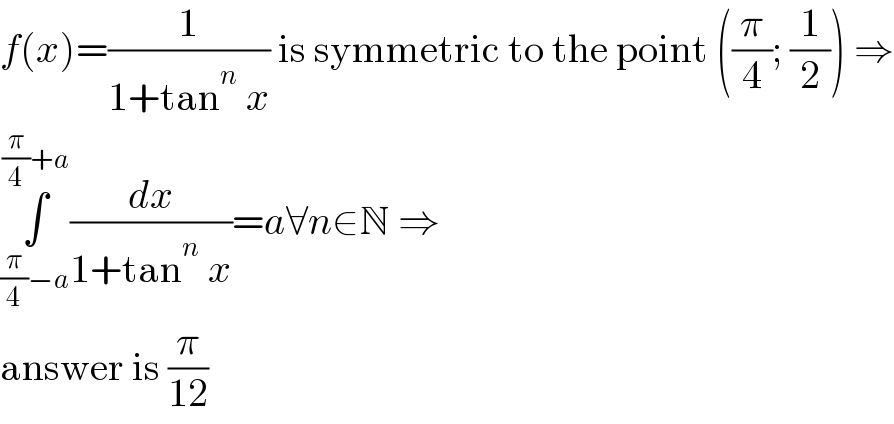 | ||
Answered by Ar Brandon last updated on 03/Dec/22 | ||
![I=∫_(π/6) ^(π/3) (1/(1+(tanx)^(2013) ))dx I=∫_(π/6) ^(π/3) (((cosx)^(2013) )/((cosx)^(2013) +(sinx)^(2013) ))dx ...eqn(i) I=∫_(π/6) ^(π/3) (((sinx)^(2013) )/((cosx)^(2013) +(sinx)^(2013) ))dx ...eqn(ii) eqn(i)+eqn(ii) 2I=∫_(π/6) ^(π/3) (((cosx)^(2013) +(sinx)^(2013) )/((cosx)^(2013) +(sinx)^(2013) ))dx=∫_(π/6) ^(π/3) dx ⇒I=(1/2)[x]_(π/6) ^(π/3) =(1/2)((π/3)−(π/6))=(1/2)((π/6))= determinant (((π/(12))))](Q182061.png) | ||
| ||
Answered by SEKRET last updated on 04/Dec/22 | ||
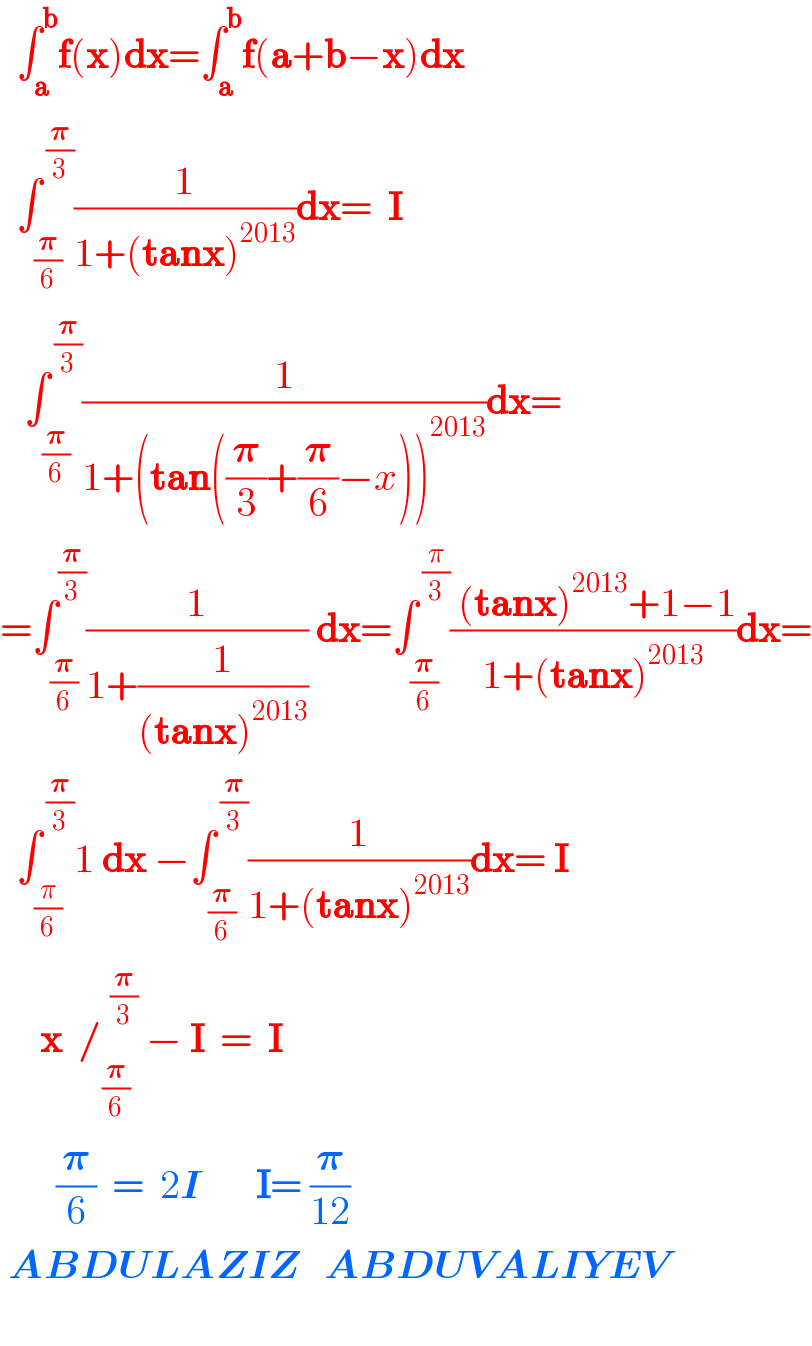 | ||
| ||