
Question Number 182149 by Acem last updated on 05/Dec/22

Commented by Acem last updated on 05/Dec/22

$$\:{Find}\:\alpha \\ $$
Answered by HeferH last updated on 05/Dec/22

$$\:{By}\:{construction}: \\ $$$$\mathrm{40}°\:−\:\alpha\:=\:\alpha\:−\:\mathrm{20}° \\ $$$$\:\alpha\:=\:\mathrm{30}° \\ $$
Commented by Acem last updated on 05/Dec/22

$$\:\mathrm{30}\:{is}\:{correct},\:{but}\:{how}? \\ $$
Answered by HeferH last updated on 05/Dec/22

Commented by Acem last updated on 05/Dec/22

$$\:{Thanks}!\:{i}'{ll}\:{check}\:{your}\:{method}\:{very}\:{soon} \\ $$$$\:{Thank}\:{you} \\ $$
Answered by a.lgnaoui last updated on 06/Dec/22
![△ABD ∡ABD=180−(80+20)=80 ⇒AD=BD AB^2 =2AD^2 (1−cos 20) AD^2 =((AB^2 )/(2(1−cos 20))) (1) △ACD CD=AB⇒ AD^2 =AC^2 +AB^2 +2AB×ACcos α △ABC ABsin 80=ACsin α (2) AD^2 =((AB^2 sin^2 80)/(sin^2 α))+AB^2 +((2AB^2 )/(sin α))×sin 80cos α =AB^2 (((sin^2 80)/(sin^2 α))+((2sin 80cos α)/(sin α))+1) =AB^2 [(((sin^2 80)/(sin^2 α))+((2sin 80cos α)/(sin α))+1]=((AB^2 )/(2(1−cos 20))) (1/(2(1−cos 20)))=((sin^2 80(1+tan^2 α))/(tan^2 α))+((2sin 80)/(tan α))+1) (1/(2(1−cos 20)))=[((sin^2 80(1+tan^2 α)+2sin 80tan α+tan^2 α)/(tan^2 α))] =[(((sin^2 80+1)tan^2 α+2sin 80tan α+sin^2 80)/(tan^2 α))] posons t=tan α t^2 =2(1−cos 20)[(sin^2 80+1)t^2 +2sin 80t+sin^2 80] 0=[2sin^2 80(1−cos 20)−2cos 20+1]t^2 +(2sin 80)t+sin^2 80 t^2 +((2sin 80)/(1+2sin^2 80(1−cos 20)−2cos 20))t+((sin^2 80)/(1+2sin^2 80(1−cos 20)−2cos 20))=0 sin 80=0,98480775 cos 20=0,939692620785 sin^2 80=0,969846310393 t^2 +((1,969615506)/(0,762407463))t+((0,96984631039)/(0,762407463)) t^2 +2,5834158258 t+1,272081764 t=0,662082972 t=3,842665708 α=tan^(−1) (t)={33,5 ; 75,5} Angle α=33,5°](Q182226.png)
$$\bigtriangleup\mathrm{ABD}\:\:\:\measuredangle\mathrm{ABD}=\mathrm{180}−\left(\mathrm{80}+\mathrm{20}\right)=\mathrm{80}\:\Rightarrow\mathrm{AD}=\mathrm{BD} \\ $$$$\mathrm{AB}^{\mathrm{2}} \:=\mathrm{2AD}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\mathrm{20}\right)\:\:\:\: \\ $$$$\mathrm{AD}^{\mathrm{2}} =\frac{\mathrm{AB}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{20}\right)}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\bigtriangleup\mathrm{ACD}\:\:\:\:\:\mathrm{CD}=\mathrm{AB}\Rightarrow\:\:\:\mathrm{AD}^{\mathrm{2}} =\mathrm{AC}^{\mathrm{2}} +\mathrm{AB}^{\mathrm{2}} +\mathrm{2AB}×\mathrm{ACcos}\:\alpha\:\: \\ $$$$\bigtriangleup\mathrm{ABC}\:\:\:\:\mathrm{ABsin}\:\mathrm{80}=\mathrm{ACsin}\:\alpha\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\:\mathrm{AD}^{\mathrm{2}} =\frac{\mathrm{AB}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \mathrm{80}}{\mathrm{sin}\:^{\mathrm{2}} \alpha}+\mathrm{AB}^{\mathrm{2}} +\frac{\mathrm{2AB}^{\mathrm{2}} }{\mathrm{sin}\:\alpha}×\mathrm{sin}\:\mathrm{80cos}\:\alpha \\ $$$$=\mathrm{AB}^{\mathrm{2}} \left(\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{80}}{\mathrm{sin}\:^{\mathrm{2}} \alpha}+\frac{\mathrm{2sin}\:\mathrm{80cos}\:\alpha}{\mathrm{sin}\:\alpha}+\mathrm{1}\right) \\ $$$$=\mathrm{AB}^{\mathrm{2}} \left[\left(\frac{\mathrm{sin}^{\mathrm{2}} \:\mathrm{80}}{\mathrm{sin}^{\mathrm{2}} \:\alpha}+\frac{\mathrm{2sin}\:\mathrm{80cos}\:\alpha}{\mathrm{sin}\:\alpha}+\mathrm{1}\right]=\frac{\mathrm{AB}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{20}\right)}\right. \\ $$$$\left.\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{20}\right)}=\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{80}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \alpha\right)}{\mathrm{tan}\:^{\mathrm{2}} \alpha}+\frac{\mathrm{2sin}\:\mathrm{80}}{\mathrm{tan}\:\alpha}+\mathrm{1}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{20}\right)}=\left[\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{80}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \alpha\right)+\mathrm{2sin}\:\mathrm{80tan}\:\alpha+\mathrm{tan}\:^{\mathrm{2}} \alpha}{\mathrm{tan}\:^{\mathrm{2}} \alpha}\right] \\ $$$$\:\:\:\:\:\:\:\:=\left[\frac{\left(\mathrm{sin}^{\mathrm{2}} \mathrm{80}+\mathrm{1}\right)\mathrm{tan}\:^{\mathrm{2}} \alpha+\mathrm{2sin}\:\mathrm{80tan}\:\alpha+\mathrm{sin}\:^{\mathrm{2}} \mathrm{80}}{\mathrm{tan}\:^{\mathrm{2}} \alpha}\right] \\ $$$${posons}\:\:{t}=\mathrm{tan}\:\alpha \\ $$$${t}^{\mathrm{2}} =\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{20}\right)\left[\left(\mathrm{sin}\:^{\mathrm{2}} \mathrm{80}+\mathrm{1}\right){t}^{\mathrm{2}} +\mathrm{2sin}\:\mathrm{80}{t}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{80}\right] \\ $$$$\mathrm{0}=\left[\mathrm{2sin}\:^{\mathrm{2}} \mathrm{80}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{20}\right)−\mathrm{2cos}\:\mathrm{20}+\mathrm{1}\right]{t}^{\mathrm{2}} +\left(\mathrm{2sin}\:\mathrm{80}\right){t}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{80} \\ $$$${t}^{\mathrm{2}} +\frac{\mathrm{2sin}\:\mathrm{80}}{\mathrm{1}+\mathrm{2sin}\:^{\mathrm{2}} \mathrm{80}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{20}\right)−\mathrm{2cos}\:\mathrm{20}}{t}+\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{80}}{\mathrm{1}+\mathrm{2sin}\:^{\mathrm{2}} \mathrm{80}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{20}\right)−\mathrm{2cos}\:\mathrm{20}}=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{sin}\:\mathrm{80}=\mathrm{0},\mathrm{98480775}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\mathrm{20}=\mathrm{0},\mathrm{939692620785} \\ $$$$\mathrm{sin}\:^{\mathrm{2}} \mathrm{80}=\mathrm{0},\mathrm{969846310393} \\ $$$$ \\ $$$${t}^{\mathrm{2}} +\frac{\mathrm{1},\mathrm{969615506}}{\mathrm{0},\mathrm{762407463}}{t}+\frac{\mathrm{0},\mathrm{96984631039}}{\mathrm{0},\mathrm{762407463}} \\ $$$$ \\ $$$$\boldsymbol{{t}}^{\mathrm{2}} +\mathrm{2},\mathrm{5834158258}\:\:\boldsymbol{{t}}+\mathrm{1},\mathrm{272081764} \\ $$$${t}=\mathrm{0},\mathrm{662082972} \\ $$$${t}=\mathrm{3},\mathrm{842665708} \\ $$$$\alpha=\mathrm{tan}^{−\mathrm{1}} \left({t}\right)=\left\{\mathrm{33},\mathrm{5}\:\:;\:\:\mathrm{75},\mathrm{5}\right\} \\ $$$${Angle}\:\:\alpha=\mathrm{33},\mathrm{5}°\:\:\:\: \\ $$$$ \\ $$
Commented by a.lgnaoui last updated on 06/Dec/22
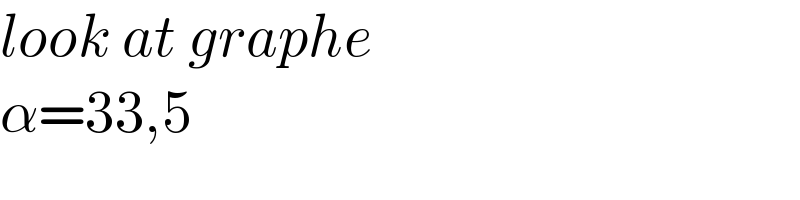
$${look}\:{at}\:{graphe} \\ $$$$\alpha=\mathrm{33},\mathrm{5} \\ $$
Commented by a.lgnaoui last updated on 06/Dec/22

Commented by Acem last updated on 06/Dec/22

$$\:{Monsieur}\:{Ignaoui},\:{merci}\:{beaucoup}\:{pour}\:{partage}' \\ $$$$\:{Il}\:{est}\:{possible}\:{qu}'{il}\:{y}\:{ait}\:{eu}\:{une}\:{erreur}\:{lors} \\ $$$$\:{du}\:{calcul},\:{l}'{angle}\:{est}\:\mathrm{30}°\: \\ $$$$\:{Vous}\:{pouvez}\:{ve}'{rifier}\:{la}\:{solution}\:{selon}\:{la} \\ $$$$\:{me}'{thode}\:{Euclidienne}\:{ci}−{dessous} \\ $$
Commented by a.lgnaoui last updated on 06/Dec/22

$${apres}\:{verification}\:{de}\:{calculs} \\ $$$${t}^{\mathrm{2}} +\frac{\mathrm{4sin}\:\mathrm{80}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{20}\right)}{\mathrm{2sin}\:^{\mathrm{2}} \mathrm{80}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{20}\right)−\mathrm{2cos}\:\mathrm{20}+\mathrm{1}}{t}+\frac{\mathrm{2sin}\:^{\mathrm{2}} \mathrm{80}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{20}\right)}{\mathrm{2sin}\:^{\mathrm{2}} \mathrm{80}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{20}\right)−\mathrm{2cos}\:\mathrm{20}+\mathrm{1}} \\ $$$${t}^{\mathrm{2}} −\mathrm{0},\mathrm{3115980757584}\:{t}−\mathrm{0},\mathrm{1534321003521} \\ $$$$\left\{_{{t}\mathrm{2}=−\mathrm{0},\mathrm{5315043867363}} ^{{t}_{\mathrm{1}} =\:\:+\mathrm{0},\mathrm{5773502691266}} \right. \\ $$$${soit}\:\:\:\:\:\alpha=\mathrm{29},\mathrm{99999} \\ $$$$\:\:{donc}\:\:\alpha=\mathrm{30}\:\:{est}\:{solution} \\ $$$$ \\ $$$${autre}=−\mathrm{28}\left({exclu}\right) \\ $$
Answered by Acem last updated on 06/Dec/22

Commented by Acem last updated on 06/Dec/22
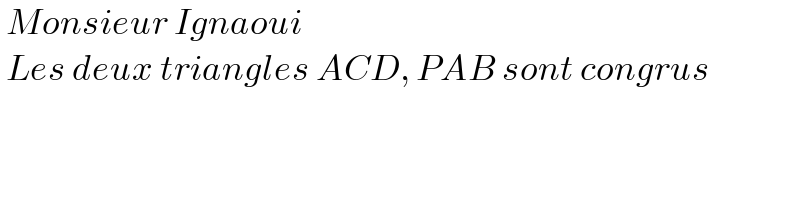
$$\:{Monsieur}\:{Ignaoui} \\ $$$$\:{Les}\:{deux}\:{triangles}\:{ACD},\:{PAB}\:{sont}\:{congrus} \\ $$$$ \\ $$
Commented by a.lgnaoui last updated on 06/Dec/22
$${je}\:{verifie}\:{les}\:{calculs} \\ $$
