
Question Number 18223 by Arnab Maiti last updated on 17/Jul/17
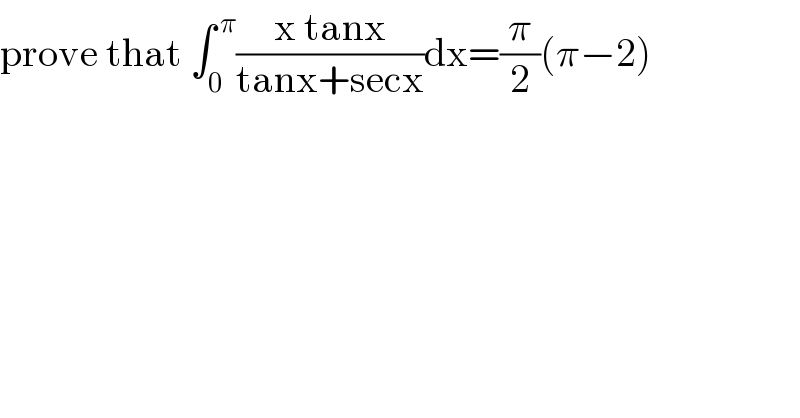
$$\mathrm{prove}\:\mathrm{that}\:\int_{\mathrm{0}} ^{\:\pi} \frac{\mathrm{x}\:\mathrm{tanx}}{\mathrm{tanx}+\mathrm{secx}}\mathrm{dx}=\frac{\pi}{\mathrm{2}}\left(\pi−\mathrm{2}\right) \\ $$
Answered by alex041103 last updated on 17/Jul/17
![First we will integrate by parts u=x dv=((tan x)/(tan x + sec x)) du=dx Now ((tan x)/(tan x + sec x)) = ((tan x(sec x − tan x))/(sec^2 x − tan^2 x))= =tan x(sec x − tan x)= =sec x tan x − tan^2 x So v=sec x − tan x + x Now we integrate ∫_0 ^( π) ((x tanx)/(tanx+secx))dx= ∫_0 ^( π) x(sec x tan x − tan^2 x)dx= =x(sec x − tan x + x)_0 ^π − ∫_0 ^( π) (sec x − tan x + x)dx =π(π−1)−[ln∣sec x + tan x∣+ln∣cos x∣+(x^2 /2)]_0 ^π = =π^2 −π−[ln∣1+sin x∣+(x^2 /2)]_0 ^π = =(π^2 /2)−π=(π/2)(π−2) ⇒∫_0 ^( π) ((x tan x)/(sec x + tan x))dx = (π/2)(π−2)](Q18231.png)
$${First}\:{we}\:{will}\:{integrate}\:{by}\:{parts} \\ $$$${u}={x}\:\:\:\:{dv}=\frac{{tan}\:{x}}{{tan}\:{x}\:+\:{sec}\:{x}} \\ $$$${du}={dx} \\ $$$${Now} \\ $$$$\frac{{tan}\:{x}}{{tan}\:{x}\:+\:{sec}\:{x}}\:=\:\frac{{tan}\:{x}\left({sec}\:{x}\:−\:{tan}\:{x}\right)}{{sec}^{\mathrm{2}} {x}\:−\:{tan}^{\mathrm{2}} {x}}= \\ $$$$={tan}\:{x}\left({sec}\:{x}\:−\:{tan}\:{x}\right)= \\ $$$$={sec}\:{x}\:{tan}\:{x}\:−\:{tan}^{\mathrm{2}} {x} \\ $$$${So}\:{v}={sec}\:{x}\:−\:{tan}\:{x}\:+\:{x} \\ $$$${Now}\:{we}\:{integrate}\: \\ $$$$\int_{\mathrm{0}} ^{\:\pi} \frac{\mathrm{x}\:\mathrm{tanx}}{\mathrm{tanx}+\mathrm{secx}}\mathrm{dx}= \\ $$$$\int_{\mathrm{0}} ^{\:\pi} {x}\left({sec}\:{x}\:{tan}\:{x}\:−\:{tan}^{\mathrm{2}} {x}\right){dx}= \\ $$$$={x}\left({sec}\:{x}\:−\:{tan}\:{x}\:+\:{x}\right)_{\mathrm{0}} ^{\pi} \:−\:\int_{\mathrm{0}} ^{\:\pi} \left({sec}\:{x}\:−\:{tan}\:{x}\:+\:{x}\right){dx} \\ $$$$=\pi\left(\pi−\mathrm{1}\right)−\left[{ln}\mid{sec}\:{x}\:+\:{tan}\:{x}\mid+{ln}\mid{cos}\:{x}\mid+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\pi} = \\ $$$$=\pi^{\mathrm{2}} −\pi−\left[{ln}\mid\mathrm{1}+{sin}\:{x}\mid+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\pi} = \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{2}}−\pi=\frac{\pi}{\mathrm{2}}\left(\pi−\mathrm{2}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\:\pi} \frac{{x}\:{tan}\:{x}}{{sec}\:{x}\:+\:{tan}\:{x}}{dx}\:=\:\frac{\pi}{\mathrm{2}}\left(\pi−\mathrm{2}\right) \\ $$$$ \\ $$
Commented by Arnab Maiti last updated on 17/Jul/17
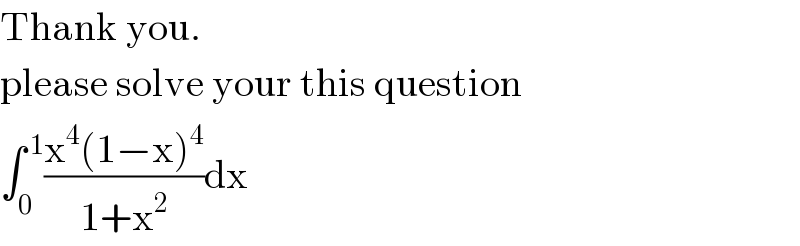
$$\mathrm{Thank}\:\mathrm{you}. \\ $$$$\mathrm{please}\:\mathrm{solve}\:\mathrm{your}\:\mathrm{this}\:\mathrm{question} \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{x}^{\mathrm{4}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{4}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$
Commented by alex041103 last updated on 17/Jul/17

$${is}\:{it}\:{Q}.\mathrm{17463} \\ $$
Commented by alex041103 last updated on 17/Jul/17

$${you}\:{can}\:{see}\:{the}\:{answer}\:{and}\:{solution}\: \\ $$$${at}\:{Q}.\mathrm{17463} \\ $$
