
Question and Answers Forum
Question Number 182374 by rs4089 last updated on 08/Dec/22

Commented by Rasheed.Sindhi last updated on 08/Dec/22

Answered by Rasheed.Sindhi last updated on 09/Dec/22
![n=a^3 +b^3 =(a+b)(a^2 −ab+b^2 ) ∵ a+b≤a^2 −ab+b^2 [see Q#182379] and 23 is the smallest prime factor of a^3 +b^3 ∴ a+b=23 with a^2 −ab+b^2 has no prime factor less than or equal to 23 Note: By {a_0 ,b_0 } we mean (a_0 ,b_0 ) or (b_0 ,a_0 ). Also we knowt If (a_0 ,b_(0 ) ) is solution so the (b_0 ,a_0 ). Case:{a,b}={1,22} a^2 −ab+b^2 =463=463 ✓ Case:{a,b}={2,21} a^2 −ab+b^2 =403=13_(<23) ×31 × Case:{a,b}={3,20} a^2 −ab+b^2 =349=349 ✓ Case:{a,b}={4,19} a^2 −ab+b^2 =301= 7_(<23) ×43 × Case:{a,b}={5,18} a^2 −ab+b^2 =259=7_(<23) ×37 Case:{a,b}={6,17} a^2 −ab+b^2 =223=223 ✓ Case:{a,b}={7,16} a^2 −ab+b^2 =193=193 ✓ Case:{a,b}={8,15} a^2 −ab+b^2 =169=13_(<23) ×13 Case:{a,b}={9,14} a^2 −ab+b^2 =151=151 ✓ Case:{a,b}={10,13}_(−) a^2 −ab+b^2 =139=139_(−) ✓ Case:{a,b}={11,12} a^2 −ab+b^2 =133=7_(<23) ×19 In underlined case a^2 −ab+b^2 has no prime factor≤23 and also 139 the least number. Hence 23×139=3197 is least value of n and {a,b}={10,13} n=a^3 +b^3 =(a+b)(a^2 −ab+b^2 )=23∙139=3197](Q182420.png)
Answered by Rasheed.Sindhi last updated on 11/Dec/22
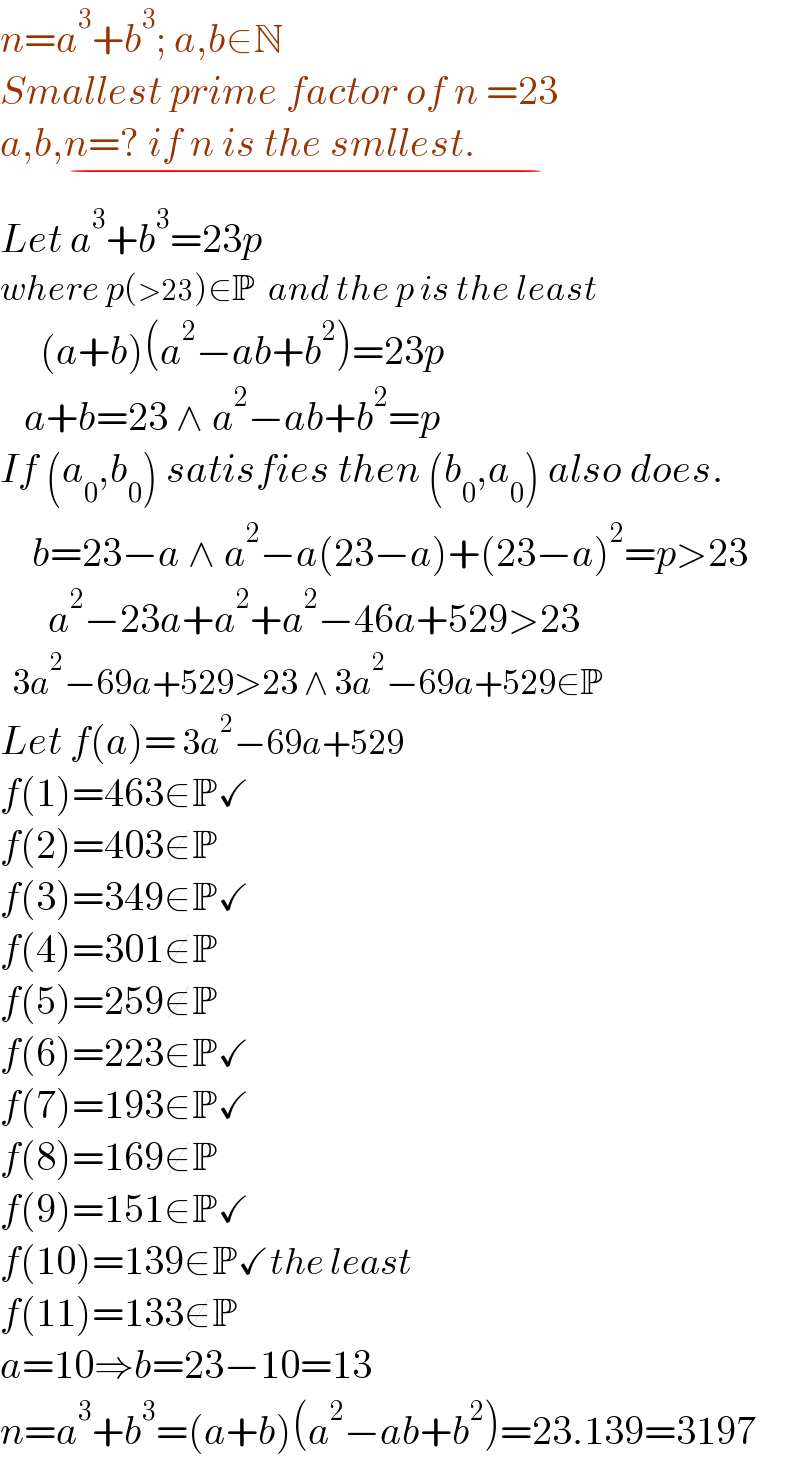
| ||
Question and Answers Forum | ||
Question Number 182374 by rs4089 last updated on 08/Dec/22 | ||
 | ||
Commented by Rasheed.Sindhi last updated on 08/Dec/22 | ||
 | ||
Answered by Rasheed.Sindhi last updated on 09/Dec/22 | ||
![n=a^3 +b^3 =(a+b)(a^2 −ab+b^2 ) ∵ a+b≤a^2 −ab+b^2 [see Q#182379] and 23 is the smallest prime factor of a^3 +b^3 ∴ a+b=23 with a^2 −ab+b^2 has no prime factor less than or equal to 23 Note: By {a_0 ,b_0 } we mean (a_0 ,b_0 ) or (b_0 ,a_0 ). Also we knowt If (a_0 ,b_(0 ) ) is solution so the (b_0 ,a_0 ). Case:{a,b}={1,22} a^2 −ab+b^2 =463=463 ✓ Case:{a,b}={2,21} a^2 −ab+b^2 =403=13_(<23) ×31 × Case:{a,b}={3,20} a^2 −ab+b^2 =349=349 ✓ Case:{a,b}={4,19} a^2 −ab+b^2 =301= 7_(<23) ×43 × Case:{a,b}={5,18} a^2 −ab+b^2 =259=7_(<23) ×37 Case:{a,b}={6,17} a^2 −ab+b^2 =223=223 ✓ Case:{a,b}={7,16} a^2 −ab+b^2 =193=193 ✓ Case:{a,b}={8,15} a^2 −ab+b^2 =169=13_(<23) ×13 Case:{a,b}={9,14} a^2 −ab+b^2 =151=151 ✓ Case:{a,b}={10,13}_(−) a^2 −ab+b^2 =139=139_(−) ✓ Case:{a,b}={11,12} a^2 −ab+b^2 =133=7_(<23) ×19 In underlined case a^2 −ab+b^2 has no prime factor≤23 and also 139 the least number. Hence 23×139=3197 is least value of n and {a,b}={10,13} n=a^3 +b^3 =(a+b)(a^2 −ab+b^2 )=23∙139=3197](Q182420.png) | ||
| ||
Answered by Rasheed.Sindhi last updated on 11/Dec/22 | ||
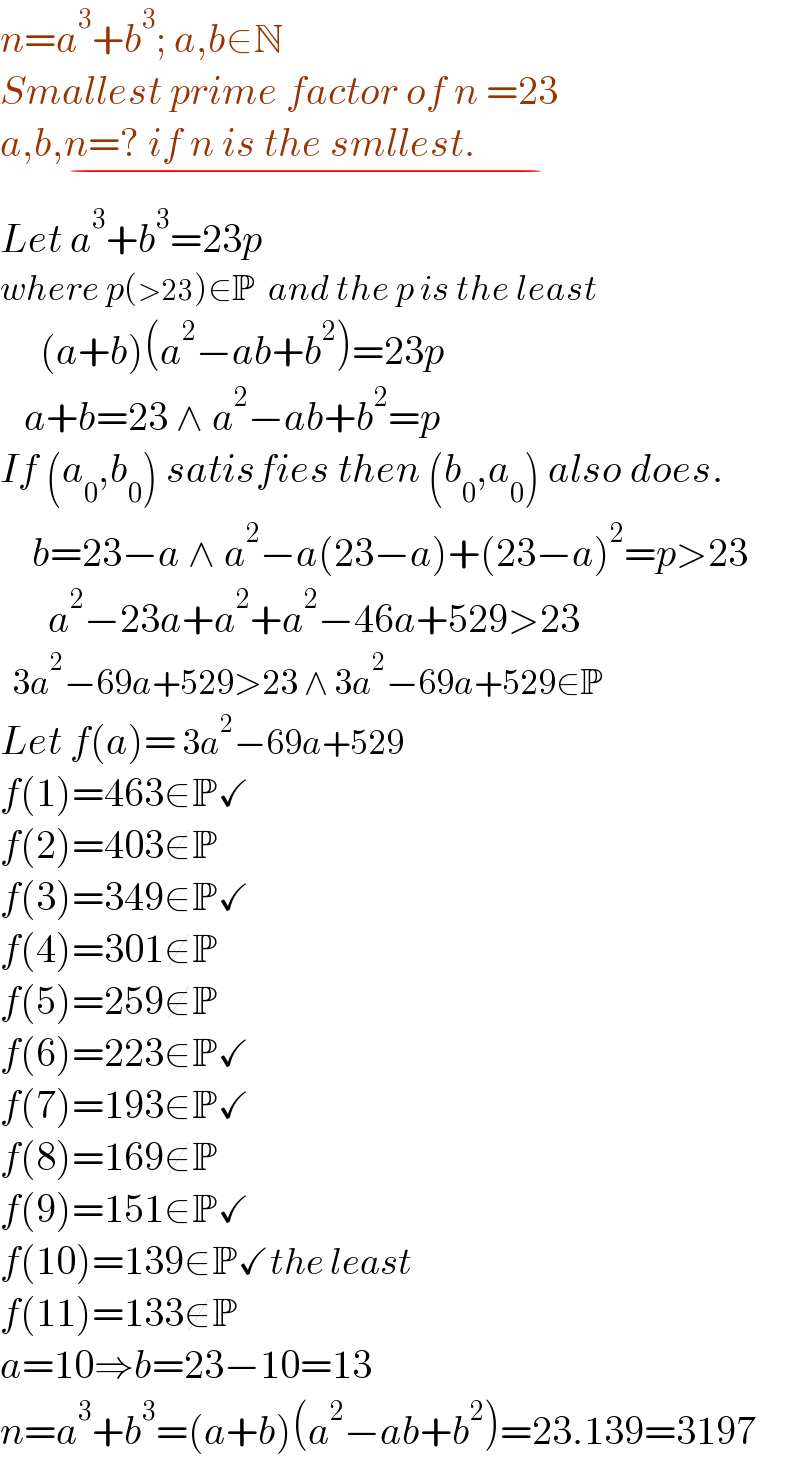 | ||
| ||