
Question and Answers Forum
Question Number 18243 by ajfour last updated on 17/Jul/17
Commented by ajfour last updated on 17/Jul/17
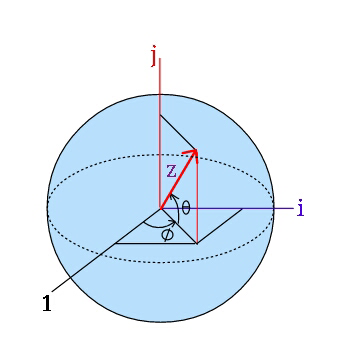
![If z=∣z∣(e^(i𝛗) cos θ+jsin θ) z_(𝛗+△𝛗) =∣z∣(e^(i𝛗+i△𝛗) cos θ+jsin θ) z^(θ+△θ) =∣z∣[e^(i𝛗) cos (θ+△θ)+jsin (θ+△θ)] Then prove : (i)z^(θ+△θ) =(cos △θ)z+(sin △θ)(∂z/∂θ) (ii)z_(𝛗+△𝛗) =(cos △𝛗)z+ (sin △𝛗)(∂z/∂𝛗)+j(1−cos △𝛗)sin θ (iii) i^2 =−1 ; find j^2 Prove z_(𝛗+△𝛗) ^(θ+△θ) =(cos △θ)z_(𝛗+△𝛗) + (sin △θ)((∂z/∂θ))_(𝛗+△𝛗) .](Q18244.png)
Commented by ajfour last updated on 09/Jul/18
| ||
Question and Answers Forum | ||
Question Number 18243 by ajfour last updated on 17/Jul/17 | ||
 | ||
Commented by ajfour last updated on 17/Jul/17 | ||
![If z=∣z∣(e^(i𝛗) cos θ+jsin θ) z_(𝛗+△𝛗) =∣z∣(e^(i𝛗+i△𝛗) cos θ+jsin θ) z^(θ+△θ) =∣z∣[e^(i𝛗) cos (θ+△θ)+jsin (θ+△θ)] Then prove : (i)z^(θ+△θ) =(cos △θ)z+(sin △θ)(∂z/∂θ) (ii)z_(𝛗+△𝛗) =(cos △𝛗)z+ (sin △𝛗)(∂z/∂𝛗)+j(1−cos △𝛗)sin θ (iii) i^2 =−1 ; find j^2 Prove z_(𝛗+△𝛗) ^(θ+△θ) =(cos △θ)z_(𝛗+△𝛗) + (sin △θ)((∂z/∂θ))_(𝛗+△𝛗) .](Q18244.png) | ||
Commented by ajfour last updated on 09/Jul/18 | ||
 | ||