
Question and Answers Forum
Question Number 182432 by SANOGO last updated on 09/Dec/22
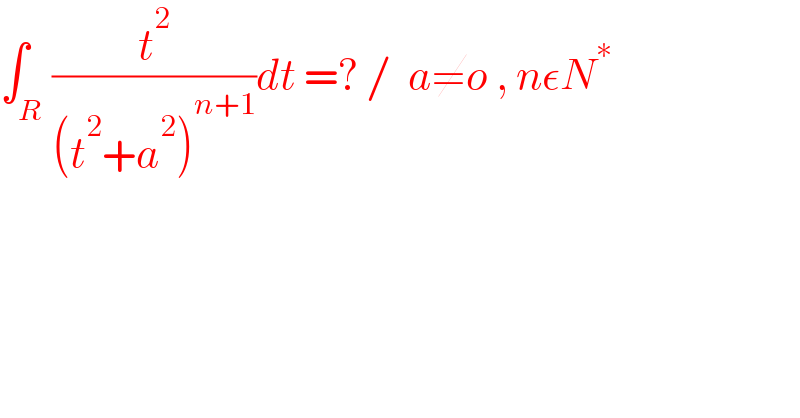
Answered by dre23 last updated on 10/Dec/22
![t=∣a∣s =∫_(−∞) ^∞ ((s^2 ∣a∣)/(a^(2n) (1+s^2 )^(n+1) ))ds,s=tg(z) =((2∣a∣)/a^(2n) )∫_0 ^(π/2) sin^2 (z)cos^(2n) (z)dz=A β(x,y)=2∫_0 ^(π/2) cos^(2x−1) (t)sin^(2y−1) (t)dt A=((∣a∣)/a^(2n) )β(2n+(1/2),1+(1/2))=((∣a∣)/a^(2n) ).((Γ(2n+(1/2))Γ(1+(1/2)))/(Γ(2n+2))) =((∣a∣[Π_(k=0) ^(2n−1) (k+(1/2))]Γ((1/2)).(1/2)Γ((1/2)))/(a^(2n) (2n+1)!)) =((π∣a∣Π_(k=0) ^n (2k+1))/(2^(2n+1) a^(2n) (2n+1)!))=((π∣a∣)/(2^(2n+1) a^(2n) 2^n n!)) =((π∣a∣)/(2^(3n+1) a^(2n) .n!))](Q182505.png)
Commented by SANOGO last updated on 11/Dec/22
Commented by dre23 last updated on 14/Dec/22

| ||
Question and Answers Forum | ||
Question Number 182432 by SANOGO last updated on 09/Dec/22 | ||
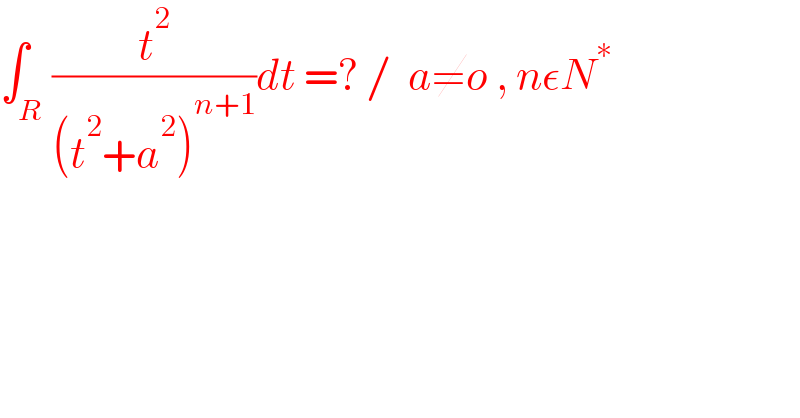 | ||
Answered by dre23 last updated on 10/Dec/22 | ||
![t=∣a∣s =∫_(−∞) ^∞ ((s^2 ∣a∣)/(a^(2n) (1+s^2 )^(n+1) ))ds,s=tg(z) =((2∣a∣)/a^(2n) )∫_0 ^(π/2) sin^2 (z)cos^(2n) (z)dz=A β(x,y)=2∫_0 ^(π/2) cos^(2x−1) (t)sin^(2y−1) (t)dt A=((∣a∣)/a^(2n) )β(2n+(1/2),1+(1/2))=((∣a∣)/a^(2n) ).((Γ(2n+(1/2))Γ(1+(1/2)))/(Γ(2n+2))) =((∣a∣[Π_(k=0) ^(2n−1) (k+(1/2))]Γ((1/2)).(1/2)Γ((1/2)))/(a^(2n) (2n+1)!)) =((π∣a∣Π_(k=0) ^n (2k+1))/(2^(2n+1) a^(2n) (2n+1)!))=((π∣a∣)/(2^(2n+1) a^(2n) 2^n n!)) =((π∣a∣)/(2^(3n+1) a^(2n) .n!))](Q182505.png) | ||
| ||
Commented by SANOGO last updated on 11/Dec/22 | ||
 | ||
Commented by dre23 last updated on 14/Dec/22 | ||
 | ||