Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 182721 by mnjuly1970 last updated on 13/Dec/22

Answered by Acem last updated on 13/Dec/22

It period: T= (1/a) f(x)=1 ⇒ b=1 lim_(x→((15^( −) )/2)) f(x)= −∞ ⇒ cos πax= cos (π^( +) /2) ⇒ a<0 π a x= π/2 ± 2πk when x= ((15)/2) : a= (1/(15)) ± (4/(15)) k^(am at problem of k) this term should be negative cause a< 0 so for k=1 and with minus mark_( But why not 2, 3, ..?) a= (1/(15)) −(4/(15)) ⇒ a= ((−1)/5) f(x)= tan ((−π)/5) x +1 _(continue...) f(x)= 0 ⇒ tan (π/(15)) x = −1 = tan (((3 π)/4) +πk) According to the diagram k=0 , k=1 x_A = ((45)/4) , x_B = ((105)/4) ⇒ Σ= ((75)/2) ≠ {a, b, c, d}

$$\:{It}\:{period}:\:{T}=\:\frac{\mathrm{1}}{{a}} \\ $$$$\:{f}\left({x}\right)=\mathrm{1}\:\Rightarrow\:{b}=\mathrm{1} \\ $$$$\underset{{x}\rightarrow\frac{\mathrm{15}^{\:−} }{\mathrm{2}}} {\mathrm{lim}}\:{f}\left({x}\right)=\:−\infty\:\Rightarrow\:\mathrm{cos}\:\pi{ax}=\:\mathrm{cos}\:\frac{\pi^{\:+} }{\mathrm{2}}\:\Rightarrow\:{a}<\mathrm{0} \\ $$$$\:\pi\:{a}\:{x}=\:\pi/\mathrm{2}\:\pm\:\mathrm{2}\pi{k} \\ $$$$\:{when}\:{x}=\:\frac{\mathrm{15}}{\mathrm{2}}\::\:{a}=\:\frac{\mathrm{1}}{\mathrm{15}}\:\underbrace{\pm\:\frac{\mathrm{4}}{\mathrm{15}}\:{k}}\:^{{am}\:{at}\:{problem}\:{of}\:{k}} \\ $$$$\:{this}\:{term}\:{should}\:{be}\:{negative}\:{cause}\:{a}<\:\mathrm{0} \\ $$$$\:{so}\:{for}\:{k}=\mathrm{1}\:{and}\:{with}\:{minus}\:{mark}_{\:{But}\:{why}\:{not}\:\mathrm{2},\:\mathrm{3},\:..?} \\ $$$$\:{a}=\:\frac{\mathrm{1}}{\mathrm{15}}\:−\frac{\mathrm{4}}{\mathrm{15}}\:\Rightarrow\:{a}=\:\frac{−\mathrm{1}}{\mathrm{5}} \\ $$$$\:{f}\left({x}\right)=\:\mathrm{tan}\:\frac{−\pi}{\mathrm{5}}\:{x}\:+\mathrm{1}\:\:_{{continue}...} \\ $$$$\: \\ $$$$\cancel{\:{f}\left({x}\right)=\:\mathrm{0}\:\Rightarrow\:\mathrm{tan}\:\frac{\pi}{\mathrm{15}}\:{x}\:=\:−\mathrm{1}\:=\:\mathrm{tan}\:\left(\frac{\mathrm{3}\:\pi}{\mathrm{4}}\:+\pi{k}\right)} \\ $$$$\:{According}\:{to}\:{the}\:{diagram}\:{k}=\mathrm{0}\:,\:{k}=\mathrm{1} \\ $$$$\cancel{\:{x}_{{A}} =\:\frac{\mathrm{45}}{\mathrm{4}}\:,\:{x}_{{B}} =\:\frac{\mathrm{105}}{\mathrm{4}}\:\Rightarrow\:\Sigma=\:\frac{\mathrm{75}}{\mathrm{2}}\:\neq\:\left\{{a},\:{b},\:{c},\:{d}\right\}} \\ $$

Answered by mahdipoor last updated on 13/Dec/22

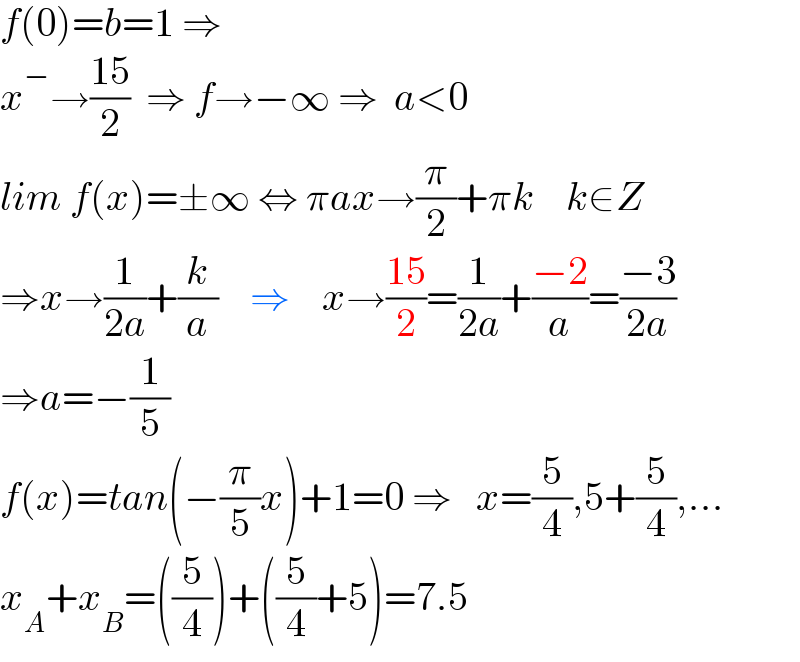
f(0)=b=1 ⇒ x^− →((15)/2) ⇒ f→−∞ ⇒ a<0 lim f(x)=±∞ ⇔ πax→(π/2)+πk k∈Z ⇒x→(1/(2a))+(k/a) ⇒ x→((15)/2)=(1/(2a))+((−2)/a)=((−3)/(2a)) ⇒a=−(1/5) f(x)=tan(−(π/5)x)+1=0 ⇒ x=(5/4),5+(5/4),... x_A +x_B =((5/4))+((5/4)+5)=7.5

$${f}\left(\mathrm{0}\right)={b}=\mathrm{1}\:\Rightarrow\: \\ $$$${x}^{−} \rightarrow\frac{\mathrm{15}}{\mathrm{2}}\:\:\Rightarrow\:{f}\rightarrow−\infty\:\Rightarrow\:\:{a}<\mathrm{0} \\ $$$${lim}\:{f}\left({x}\right)=\pm\infty\:\Leftrightarrow\:\pi{ax}\rightarrow\frac{\pi}{\mathrm{2}}+\pi{k}\:\:\:\:{k}\in{Z} \\ $$$$\Rightarrow{x}\rightarrow\frac{\mathrm{1}}{\mathrm{2}{a}}+\frac{{k}}{{a}}\:\:\:\:\Rightarrow\:\:\:\:{x}\rightarrow\frac{\mathrm{15}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}{a}}+\frac{−\mathrm{2}}{{a}}=\frac{−\mathrm{3}}{\mathrm{2}{a}} \\ $$$$\Rightarrow{a}=−\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${f}\left({x}\right)={tan}\left(−\frac{\pi}{\mathrm{5}}{x}\right)+\mathrm{1}=\mathrm{0}\:\Rightarrow\:\:\:{x}=\frac{\mathrm{5}}{\mathrm{4}},\mathrm{5}+\frac{\mathrm{5}}{\mathrm{4}},... \\ $$$${x}_{{A}} +{x}_{{B}} =\left(\frac{\mathrm{5}}{\mathrm{4}}\right)+\left(\frac{\mathrm{5}}{\mathrm{4}}+\mathrm{5}\right)=\mathrm{7}.\mathrm{5} \\ $$

Commented by Acem last updated on 13/Dec/22

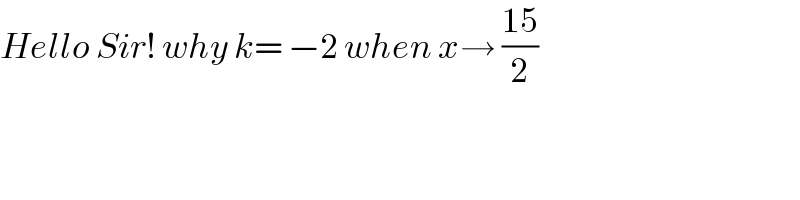
Hello Sir! why k= −2 when x→ ((15)/2)

$${Hello}\:{Sir}!\:{why}\:{k}=\:−\mathrm{2}\:{when}\:{x}\rightarrow\:\frac{\mathrm{15}}{\mathrm{2}} \\ $$

Commented by mahdipoor last updated on 13/Dec/22

Hi , when a<0 and x>0 ⇒ πax<0 in first vertical line : πax=−(π/2) and in secend line : πax=((−π)/2)−π=((−3π)/2) ... x=((15)/2) is secend line so πax=(π/2)+kπ=((−3π)/2) ⇒ k=−2

$${Hi}\:,\:{when}\:{a}<\mathrm{0}\:{and}\:{x}>\mathrm{0}\:\Rightarrow\:\pi{ax}<\mathrm{0} \\ $$$${in}\:{first}\:{vertical}\:{line}\::\:\pi{ax}=−\frac{\pi}{\mathrm{2}} \\ $$$${and}\:{in}\:{secend}\:{line}\::\:\pi{ax}=\frac{−\pi}{\mathrm{2}}−\pi=\frac{−\mathrm{3}\pi}{\mathrm{2}} \\ $$$$... \\ $$$${x}=\frac{\mathrm{15}}{\mathrm{2}}\:{is}\:{secend}\:{line}\:{so} \\ $$$$\pi{ax}=\frac{\pi}{\mathrm{2}}+{k}\pi=\frac{−\mathrm{3}\pi}{\mathrm{2}}\:\Rightarrow\:{k}=−\mathrm{2} \\ $$

Commented by Acem last updated on 13/Dec/22

Hi Sir! thank you very much In fact there are still tow problems: a• how do i know that it′s the first assymptot b• you said that πax= ((−π)/2) that mean k=−1 how do i know that k here = −1 Thought that we may can say that the 1st assymptot is when k=0 not −1

$${Hi}\:{Sir}!\:{thank}\:{you}\:{very}\:{much} \\ $$$$\:{In}\:{fact}\:{there}\:{are}\:{still}\:{tow}\:{problems}: \\ $$$$\:\:\:\:\:{a}\bullet\:{how}\:{do}\:{i}\:{know}\:{that}\:{it}'{s}\:{the}\:{first}\:{assymptot} \\ $$$$\:\:\:\:\:{b}\bullet\:{you}\:{said}\:{that}\:\pi{ax}=\:\frac{−\pi}{\mathrm{2}}\:{that}\:{mean}\:{k}=−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:{how}\:{do}\:{i}\:{know}\:{that}\:{k}\:{here}\:=\:−\mathrm{1} \\ $$$$ \\ $$$$\:\:{Thought}\:{that}\:{we}\:{may}\:{can}\:{say}\:{that}\:{the}\:\mathrm{1}{st} \\ $$$$\:{assymptot}\:{is}\:{when}\:{k}=\mathrm{0}\:{not}\:−\mathrm{1} \\ $$$$\: \\ $$

Commented by mahdipoor last updated on 14/Dec/22

[k] is not important , [πax_2 =πa((15)/2)=((−3π)/2)] is important, im say [πax=(π/2)+kπ] so k=−2 when [πax_2 =((−3π)/2)=(π/2)+(−2)π]

$$\left[{k}\right]\:{is}\:{not}\:{important}\:,\:\left[\pi{ax}_{\mathrm{2}} =\pi{a}\frac{\mathrm{15}}{\mathrm{2}}=\frac{−\mathrm{3}\pi}{\mathrm{2}}\right]\: \\ $$$${is}\:{important},\:{im}\:{say}\:\left[\pi{ax}=\frac{\pi}{\mathrm{2}}+{k}\pi\right]\:{so}\: \\ $$$${k}=−\mathrm{2}\:{when}\:\left[\pi{ax}_{\mathrm{2}} =\frac{−\mathrm{3}\pi}{\mathrm{2}}=\frac{\pi}{\mathrm{2}}+\left(−\mathrm{2}\right)\pi\right]\: \\ $$

Commented by mnjuly1970 last updated on 14/Dec/22

mamnoon jenabe mahdipoor ali bood

$${mamnoon}\:{jenabe}\:{mahdipoor}\: \\ $$$$\:\:{ali}\:{bood} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com