
Question and Answers Forum
Question Number 182786 by SANOGO last updated on 14/Dec/22
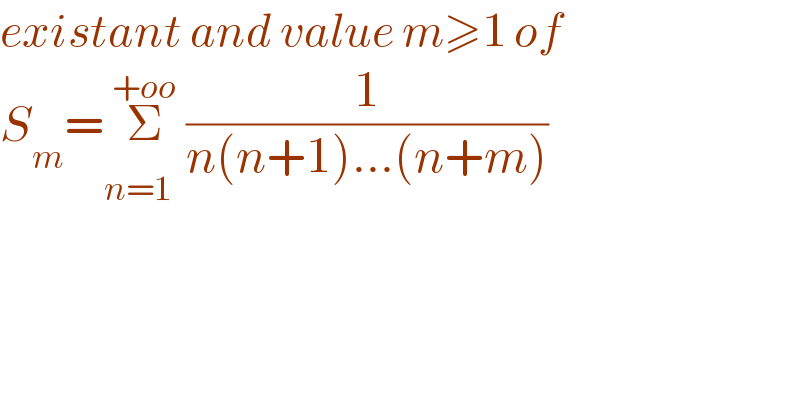
Answered by dre23 last updated on 15/Dec/22
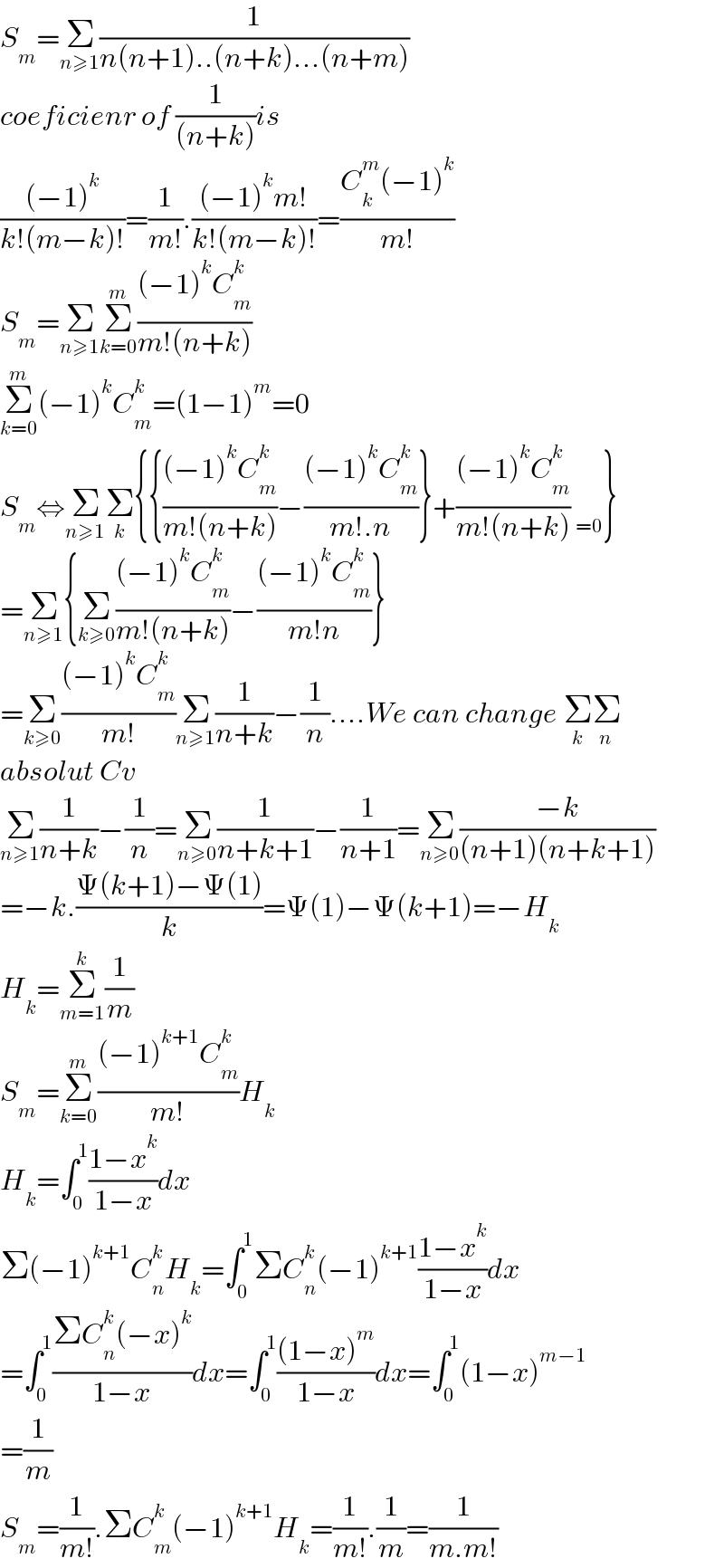
Commented by SANOGO last updated on 14/Dec/22

Commented by dre23 last updated on 16/Dec/22

Answered by mnjuly1970 last updated on 14/Dec/22
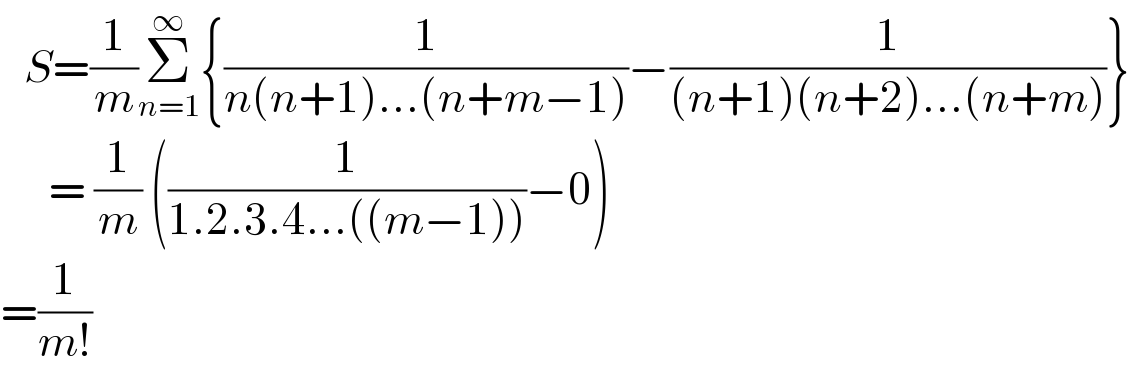
Commented by SANOGO last updated on 14/Dec/22
Commented by dre23 last updated on 15/Dec/22

