
Question and Answers Forum
Question Number 182791 by Matica last updated on 14/Dec/22
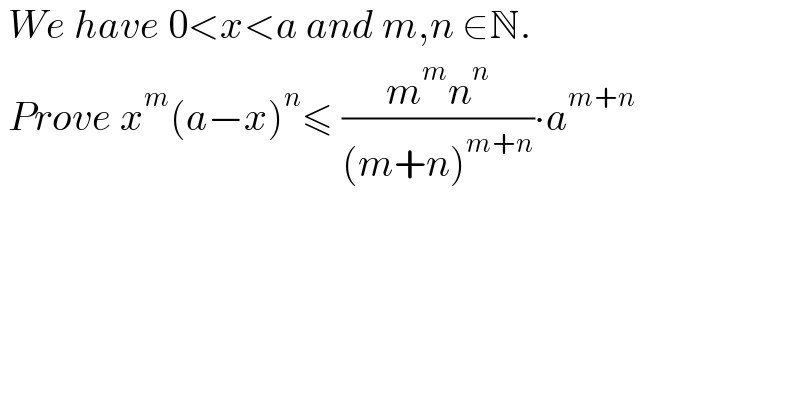
Answered by mahdipoor last updated on 14/Dec/22
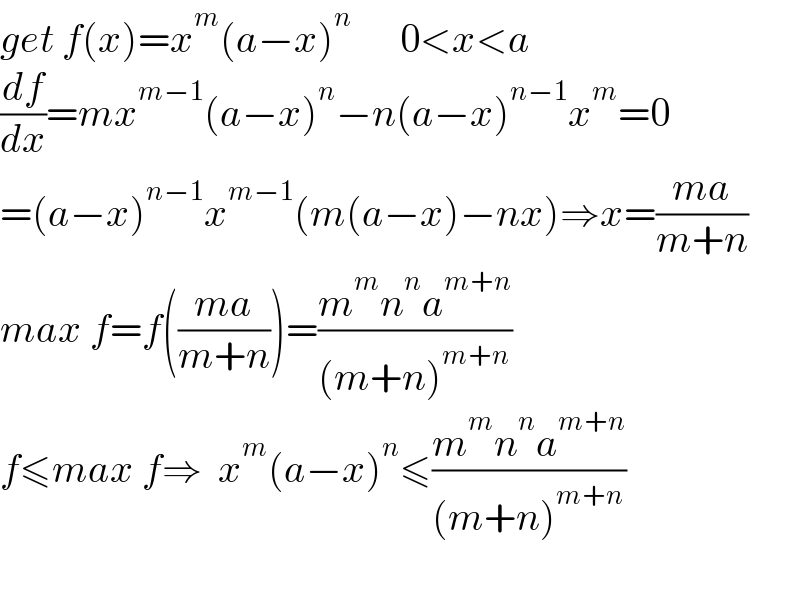
Commented byMatica last updated on 15/Dec/22

Answered by dre23 last updated on 15/Dec/22
![x^m (1−x)^n ≤((m^m n^n )/((m+n)^(m+n) )),....S by x→ax⇔∀ 0<x<1 .....S ⇔((x/m))^m (((1−x)/n))^n ≤(1/((n+m)^(n+m) ))⇔S mln((x/m))+nln(((1−x)/n))....S x→^f ln(x) is concave,f′′=−(1/x^2 )<0,∀x∈]0,1] (m/(n+m))ln((x/m))+(n/(n+m))ln(((1−x)/n))≤ln((1/(n+m))) (n+m){(m/(m+n))ln((x/m))+(n/(n+m))ln(((1−x)/n))}≤ (n+m)ln((x/(n+m))+((1−x)/(n+m)))≤(n+m)ln((1/(n+m)))=ln((1/((n+m)^(n+m) ))) ⇔s≤ln((1/((n+m)^(n+m) ))) tack e ⇔((x/m))^m (((1−x)/n))^n ≤((1/(n+m)))^(n+m) ..True](Q182844.png)
| ||
Question and Answers Forum | ||
Question Number 182791 by Matica last updated on 14/Dec/22 | ||
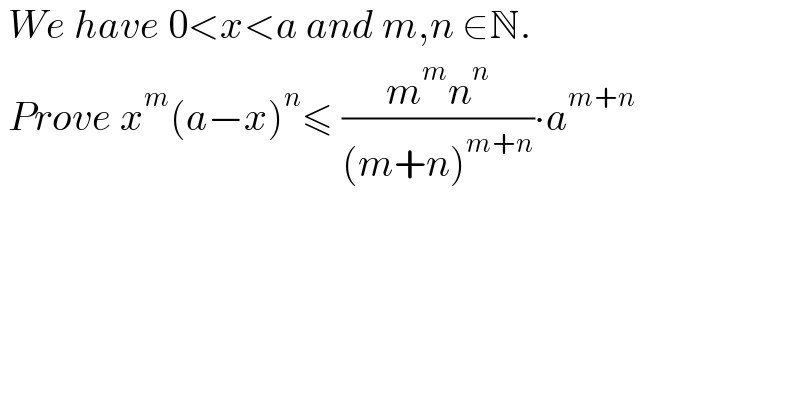 | ||
Answered by mahdipoor last updated on 14/Dec/22 | ||
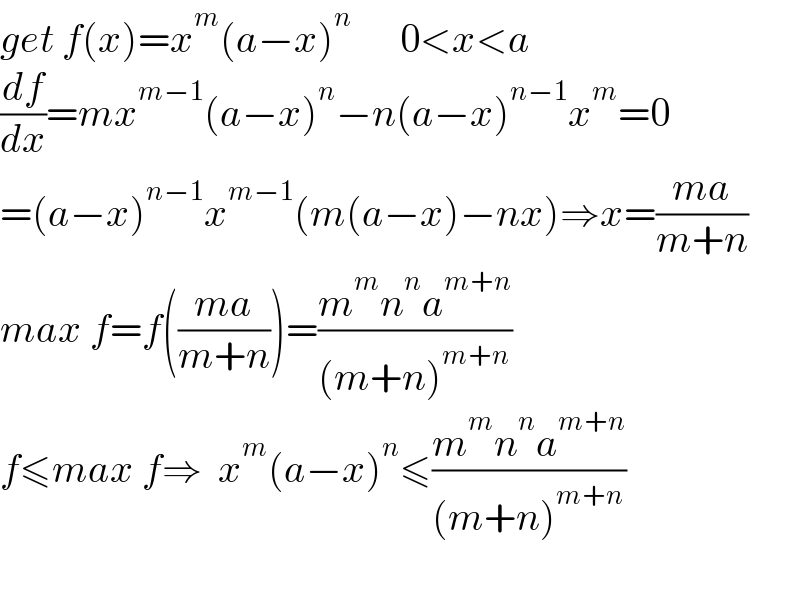 | ||
| ||
Commented byMatica last updated on 15/Dec/22 | ||
 | ||
Answered by dre23 last updated on 15/Dec/22 | ||
![x^m (1−x)^n ≤((m^m n^n )/((m+n)^(m+n) )),....S by x→ax⇔∀ 0<x<1 .....S ⇔((x/m))^m (((1−x)/n))^n ≤(1/((n+m)^(n+m) ))⇔S mln((x/m))+nln(((1−x)/n))....S x→^f ln(x) is concave,f′′=−(1/x^2 )<0,∀x∈]0,1] (m/(n+m))ln((x/m))+(n/(n+m))ln(((1−x)/n))≤ln((1/(n+m))) (n+m){(m/(m+n))ln((x/m))+(n/(n+m))ln(((1−x)/n))}≤ (n+m)ln((x/(n+m))+((1−x)/(n+m)))≤(n+m)ln((1/(n+m)))=ln((1/((n+m)^(n+m) ))) ⇔s≤ln((1/((n+m)^(n+m) ))) tack e ⇔((x/m))^m (((1−x)/n))^n ≤((1/(n+m)))^(n+m) ..True](Q182844.png) | ||
| ||