
Question and Answers Forum
Question Number 182794 by mnjuly1970 last updated on 14/Dec/22
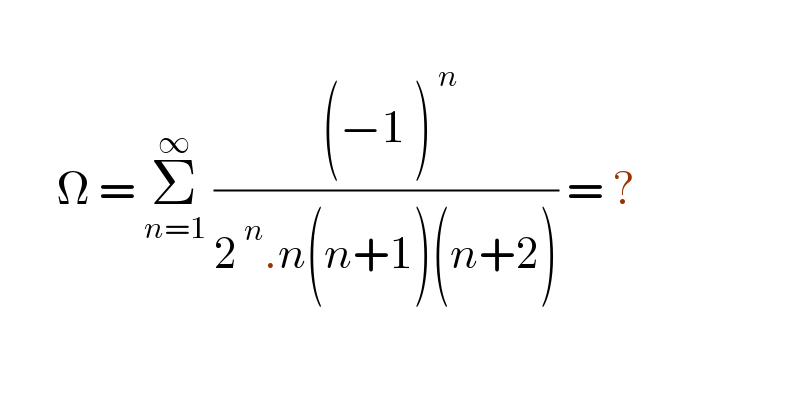
Answered by ARUNG_Brandon_MBU last updated on 14/Dec/22
![S(x)=Σ_(n=1) ^∞ (x^(n+2) /(n(n+1)(n+2))) ⇒S ′(x)=Σ_(n=1) ^∞ (x^(n+1) /(n(n+1))) ⇒S ′′(x)=Σ_(n=1) ^∞ (x^n /n) ⇒S ′′′(x)=Σ_(n=1) ^∞ x^(n−1) =(1/(1−x)) ⇒S ′′(x)=Σ_(n=1) ^∞ (x^n /n)=−ln(1−x)+C_1 , C_1 =0 ⇒S ′(x)=Σ_(n=1) ^∞ (x^(n+1) /(n(n+1)))=(1−x)ln(1−x)+x−1+C_2 , C_2 =1 ⇒S ′(x)=ln(1−x)−xln(1−x)+x ⇒S(x)=∫[−xln(1−x)+ln(1−x)+x]dx ⇒S(x)=−(x^2 /2)ln(1−x)+(1/2)((x^2 /2)+x+ln∣x−1∣) +(1−x)−(1−x)ln(1−x)+(x^2 /2)+C_3 , C_3 =−1 ⇒Σ_(n=1) ^∞ (((−1)^n )/(2^n n(n+1)(n+2)))=2^2 S(−(1/2)) =−(1/2)ln((3/2))+2((1/8)−(1/2)+ln((3/2)))+6−6ln((3/2))+(1/2)−4 ⇒Ω=(7/4)−(9/2)ln((3/2))](Q182801.png)
Commented by mnjuly1970 last updated on 14/Dec/22
| ||
Question and Answers Forum | ||
Question Number 182794 by mnjuly1970 last updated on 14/Dec/22 | ||
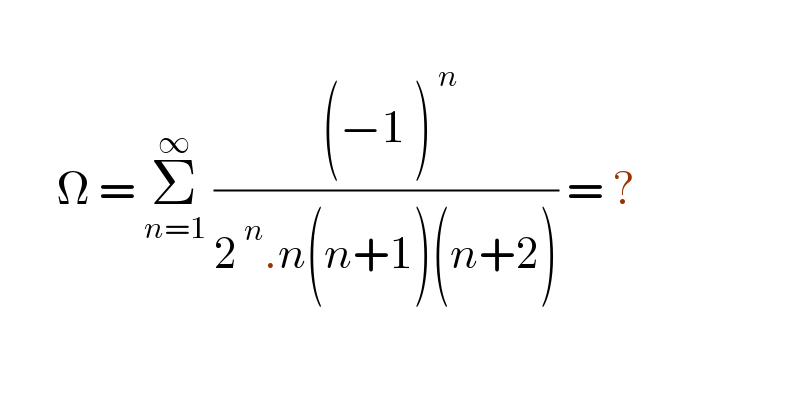 | ||
Answered by ARUNG_Brandon_MBU last updated on 14/Dec/22 | ||
![S(x)=Σ_(n=1) ^∞ (x^(n+2) /(n(n+1)(n+2))) ⇒S ′(x)=Σ_(n=1) ^∞ (x^(n+1) /(n(n+1))) ⇒S ′′(x)=Σ_(n=1) ^∞ (x^n /n) ⇒S ′′′(x)=Σ_(n=1) ^∞ x^(n−1) =(1/(1−x)) ⇒S ′′(x)=Σ_(n=1) ^∞ (x^n /n)=−ln(1−x)+C_1 , C_1 =0 ⇒S ′(x)=Σ_(n=1) ^∞ (x^(n+1) /(n(n+1)))=(1−x)ln(1−x)+x−1+C_2 , C_2 =1 ⇒S ′(x)=ln(1−x)−xln(1−x)+x ⇒S(x)=∫[−xln(1−x)+ln(1−x)+x]dx ⇒S(x)=−(x^2 /2)ln(1−x)+(1/2)((x^2 /2)+x+ln∣x−1∣) +(1−x)−(1−x)ln(1−x)+(x^2 /2)+C_3 , C_3 =−1 ⇒Σ_(n=1) ^∞ (((−1)^n )/(2^n n(n+1)(n+2)))=2^2 S(−(1/2)) =−(1/2)ln((3/2))+2((1/8)−(1/2)+ln((3/2)))+6−6ln((3/2))+(1/2)−4 ⇒Ω=(7/4)−(9/2)ln((3/2))](Q182801.png) | ||
| ||
Commented by mnjuly1970 last updated on 14/Dec/22 | ||
 | ||