Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 183044 by depressiveshrek last updated on 19/Dec/22

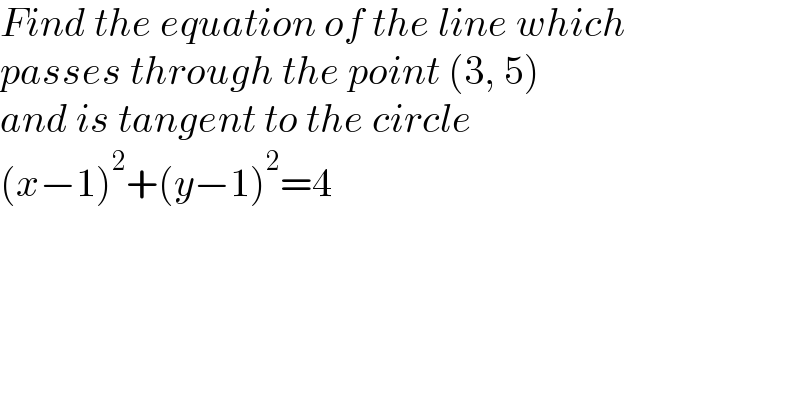
Find the equation of the line which passes through the point (3, 5) and is tangent to the circle (x−1)^2 +(y−1)^2 =4

$${Find}\:{the}\:{equation}\:{of}\:{the}\:{line}\:{which} \\ $$$${passes}\:{through}\:{the}\:{point}\:\left(\mathrm{3},\:\mathrm{5}\right) \\ $$$${and}\:{is}\:{tangent}\:{to}\:{the}\:{circle} \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4} \\ $$

Answered by mr W last updated on 19/Dec/22

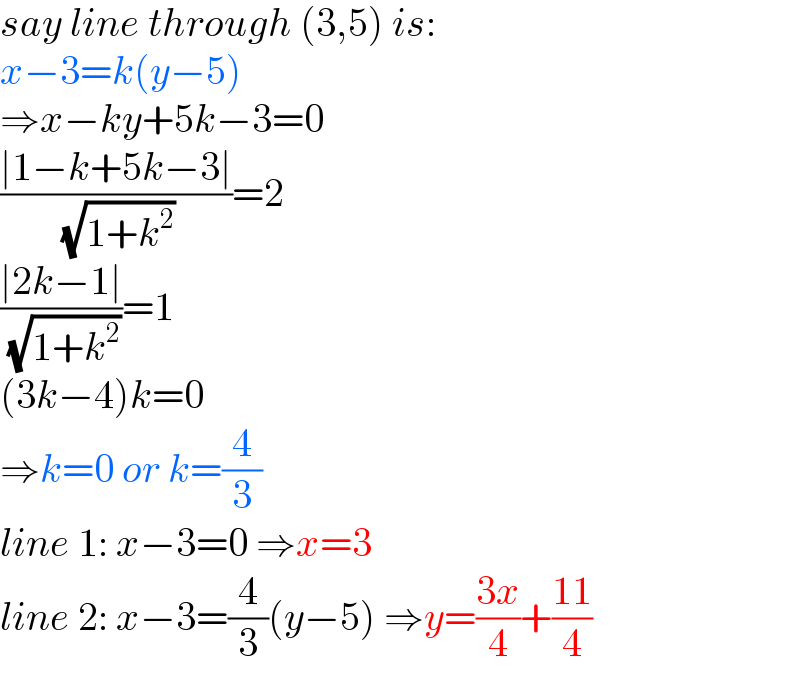
say line through (3,5) is: x−3=k(y−5) ⇒x−ky+5k−3=0 ((∣1−k+5k−3∣)/( (√(1+k^2 ))))=2 ((∣2k−1∣)/( (√(1+k^2 ))))=1 (3k−4)k=0 ⇒k=0 or k=(4/3) line 1: x−3=0 ⇒x=3 line 2: x−3=(4/3)(y−5) ⇒y=((3x)/4)+((11)/4)

$${say}\:{line}\:{through}\:\left(\mathrm{3},\mathrm{5}\right)\:{is}:\: \\ $$$${x}−\mathrm{3}={k}\left({y}−\mathrm{5}\right) \\ $$$$\Rightarrow{x}−{ky}+\mathrm{5}{k}−\mathrm{3}=\mathrm{0} \\ $$$$\frac{\mid\mathrm{1}−{k}+\mathrm{5}{k}−\mathrm{3}\mid}{\:\sqrt{\mathrm{1}+{k}^{\mathrm{2}} }}=\mathrm{2} \\ $$$$\frac{\mid\mathrm{2}{k}−\mathrm{1}\mid}{\:\sqrt{\mathrm{1}+{k}^{\mathrm{2}} }}=\mathrm{1} \\ $$$$\left(\mathrm{3}{k}−\mathrm{4}\right){k}=\mathrm{0} \\ $$$$\Rightarrow{k}=\mathrm{0}\:{or}\:{k}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${line}\:\mathrm{1}:\:{x}−\mathrm{3}=\mathrm{0}\:\Rightarrow{x}=\mathrm{3} \\ $$$${line}\:\mathrm{2}:\:{x}−\mathrm{3}=\frac{\mathrm{4}}{\mathrm{3}}\left({y}−\mathrm{5}\right)\:\Rightarrow{y}=\frac{\mathrm{3}{x}}{\mathrm{4}}+\frac{\mathrm{11}}{\mathrm{4}} \\ $$

Commented by mr W last updated on 19/Dec/22

Answered by MathAcer26 last updated on 19/Dec/22

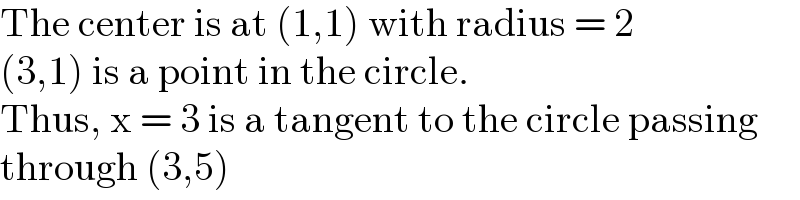
The center is at (1,1) with radius = 2 (3,1) is a point in the circle. Thus, x = 3 is a tangent to the circle passing through (3,5)

$$\mathrm{The}\:\mathrm{center}\:\mathrm{is}\:\mathrm{at}\:\left(\mathrm{1},\mathrm{1}\right)\:\mathrm{with}\:\mathrm{radius}\:=\:\mathrm{2} \\ $$$$\left(\mathrm{3},\mathrm{1}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{point}\:\mathrm{in}\:\mathrm{the}\:\mathrm{circle}. \\ $$$$\mathrm{Thus},\:\mathrm{x}\:=\:\mathrm{3}\:\mathrm{is}\:\mathrm{a}\:\mathrm{tangent}\:\mathrm{to}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{passing} \\ $$$$\mathrm{through}\:\left(\mathrm{3},\mathrm{5}\right) \\ $$

Answered by ajfour last updated on 20/Dec/22

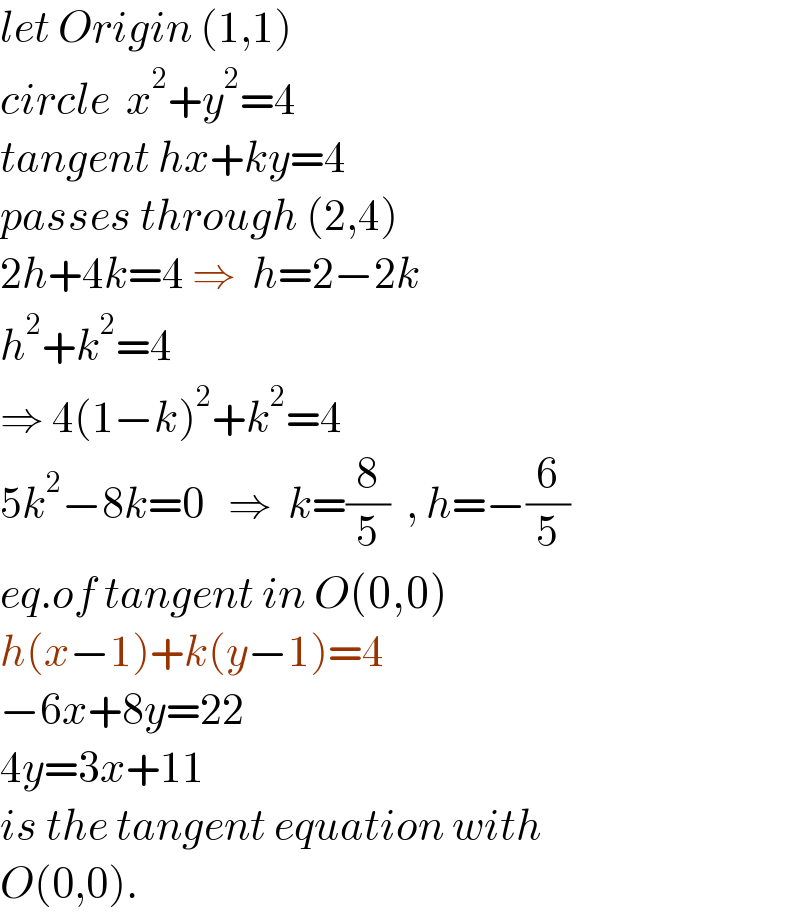
let Origin (1,1) circle x^2 +y^2 =4 tangent hx+ky=4 passes through (2,4) 2h+4k=4 ⇒ h=2−2k h^2 +k^2 =4 ⇒ 4(1−k)^2 +k^2 =4 5k^2 −8k=0 ⇒ k=(8/5) , h=−(6/5) eq.of tangent in O(0,0) h(x−1)+k(y−1)=4 −6x+8y=22 4y=3x+11 is the tangent equation with O(0,0).

$${let}\:{Origin}\:\left(\mathrm{1},\mathrm{1}\right) \\ $$$${circle}\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{4} \\ $$$${tangent}\:{hx}+{ky}=\mathrm{4} \\ $$$${passes}\:{through}\:\left(\mathrm{2},\mathrm{4}\right) \\ $$$$\mathrm{2}{h}+\mathrm{4}{k}=\mathrm{4}\:\Rightarrow\:\:{h}=\mathrm{2}−\mathrm{2}{k} \\ $$$${h}^{\mathrm{2}} +{k}^{\mathrm{2}} =\mathrm{4} \\ $$$$\Rightarrow\:\mathrm{4}\left(\mathrm{1}−{k}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} =\mathrm{4} \\ $$$$\mathrm{5}{k}^{\mathrm{2}} −\mathrm{8}{k}=\mathrm{0}\:\:\:\Rightarrow\:\:{k}=\frac{\mathrm{8}}{\mathrm{5}}\:\:,\:{h}=−\frac{\mathrm{6}}{\mathrm{5}} \\ $$$${eq}.{of}\:{tangent}\:{in}\:{O}\left(\mathrm{0},\mathrm{0}\right) \\ $$$${h}\left({x}−\mathrm{1}\right)+{k}\left({y}−\mathrm{1}\right)=\mathrm{4} \\ $$$$−\mathrm{6}{x}+\mathrm{8}{y}=\mathrm{22} \\ $$$$\mathrm{4}{y}=\mathrm{3}{x}+\mathrm{11} \\ $$$${is}\:{the}\:{tangent}\:{equation}\:{with} \\ $$$${O}\left(\mathrm{0},\mathrm{0}\right). \\ $$

Answered by cortano1 last updated on 20/Dec/22

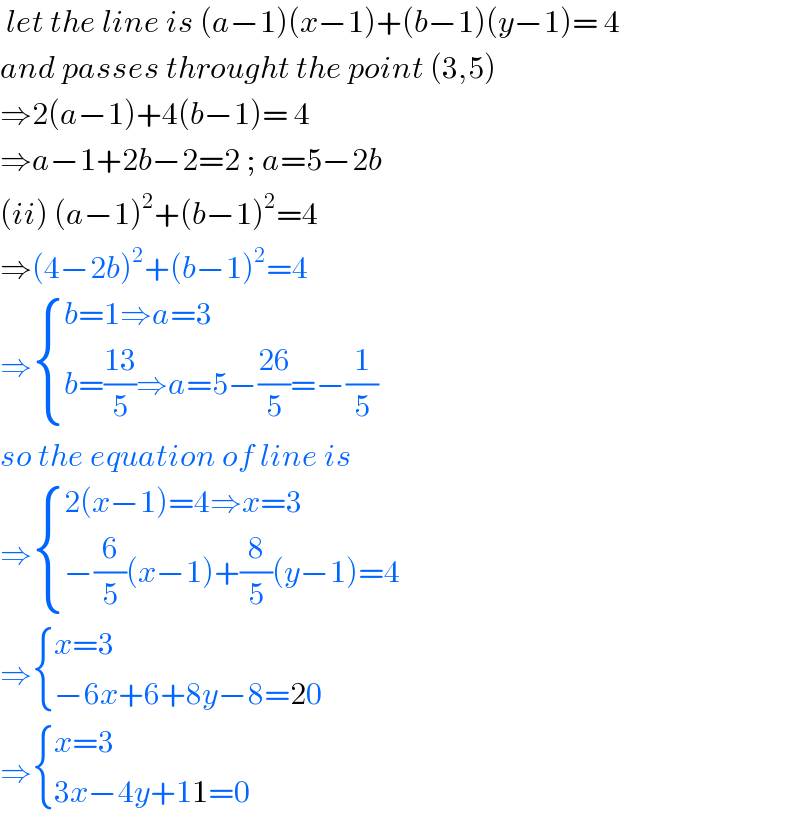
let the line is (a−1)(x−1)+(b−1)(y−1)= 4 and passes throught the point (3,5) ⇒2(a−1)+4(b−1)= 4 ⇒a−1+2b−2=2 ; a=5−2b (ii) (a−1)^2 +(b−1)^2 =4 ⇒(4−2b)^2 +(b−1)^2 =4 ⇒ { ((b=1⇒a=3)),((b=((13)/5)⇒a=5−((26)/5)=−(1/5))) :} so the equation of line is ⇒ { ((2(x−1)=4⇒x=3)),((−(6/5)(x−1)+(8/5)(y−1)=4)) :} ⇒ { ((x=3)),((−6x+6+8y−8=20)) :} ⇒ { ((x=3)),((3x−4y+11=0)) :}

$$\:{let}\:{the}\:{line}\:{is}\:\left({a}−\mathrm{1}\right)\left({x}−\mathrm{1}\right)+\left({b}−\mathrm{1}\right)\left({y}−\mathrm{1}\right)=\:\mathrm{4} \\ $$$${and}\:{passes}\:{throught}\:{the}\:{point}\:\left(\mathrm{3},\mathrm{5}\right) \\ $$$$\Rightarrow\mathrm{2}\left({a}−\mathrm{1}\right)+\mathrm{4}\left({b}−\mathrm{1}\right)=\:\mathrm{4} \\ $$$$\Rightarrow{a}−\mathrm{1}+\mathrm{2}{b}−\mathrm{2}=\mathrm{2}\:;\:{a}=\mathrm{5}−\mathrm{2}{b} \\ $$$$\left({ii}\right)\:\left({a}−\mathrm{1}\right)^{\mathrm{2}} +\left({b}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4} \\ $$$$\Rightarrow\left(\mathrm{4}−\mathrm{2}{b}\right)^{\mathrm{2}} +\left({b}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4} \\ $$$$\Rightarrow\begin{cases}{{b}=\mathrm{1}\Rightarrow{a}=\mathrm{3}}\\{{b}=\frac{\mathrm{13}}{\mathrm{5}}\Rightarrow{a}=\mathrm{5}−\frac{\mathrm{26}}{\mathrm{5}}=−\frac{\mathrm{1}}{\mathrm{5}}}\end{cases} \\ $$$${so}\:{the}\:{equation}\:{of}\:{line}\:{is} \\ $$$$\Rightarrow\begin{cases}{\mathrm{2}\left({x}−\mathrm{1}\right)=\mathrm{4}\Rightarrow{x}=\mathrm{3}}\\{−\frac{\mathrm{6}}{\mathrm{5}}\left({x}−\mathrm{1}\right)+\frac{\mathrm{8}}{\mathrm{5}}\left({y}−\mathrm{1}\right)=\mathrm{4}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{{x}=\mathrm{3}}\\{−\mathrm{6}{x}+\mathrm{6}+\mathrm{8}{y}−\mathrm{8}=\mathrm{20}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{{x}=\mathrm{3}}\\{\mathrm{3}{x}−\mathrm{4}{y}+\mathrm{11}=\mathrm{0}}\end{cases} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com