
Question and Answers Forum
Question Number 183320 by mathlove last updated on 25/Dec/22
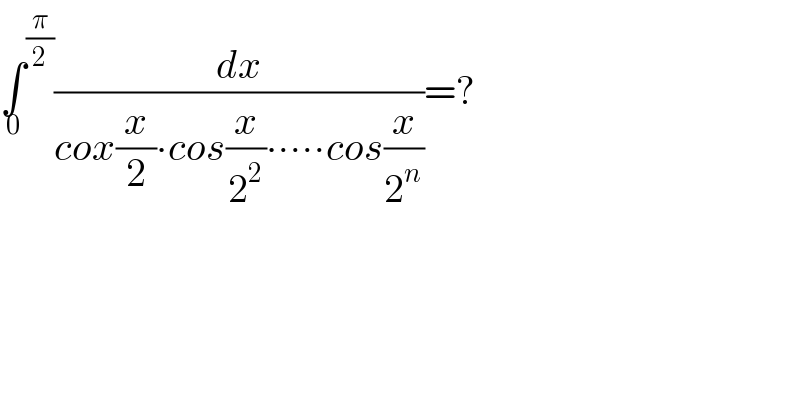
Answered by Vynho last updated on 28/Dec/22
![∫_0 ^(π/2) (dx/(Π_(k=1) ^n cos((x/2^k )))) ln(Π_(k=1) ^n cos((x/2^k )))=Σ_(k=1) ^n ln(cos((x/2^k ))) Π_(k=1) ^n cos((x/a^k ))+isin((x/a^k ))=Π_(k=1) ^n e^(i(x/a^k )) U_n =Π_(k=1) ^n e^(ix((1/a))^k ) ln(U_n )=Σ_(k=1) ^n ln(e^(ix((1/a))^k ) )=ixΣ_(k=1) ^n ((1/a))^k ln(U_n )=ix(1/a).((1−((1/a))^n )/(1−(1/a)))=ix.((1−((1/a))^n )/(a−1)) U_n =e^(ix((1−((1/a))^n )/(a−1))) ∫_0 ^(π/2) e^(−ix((1−((1/a))^n )/(a−1))) dx=∫_0 ^(π/2) e^(−ixθ) dx=(1/(−iθ))[e^(−ixθ) ]_0 ^(π/2) I=(i/θ)[e^(−i(π/2)θ) −1]=(1/θ)[icos((π/2)θ)+sin((π/2)θ)] ∫_0 ^(π/2) (dx/(Π_(k=1) ^n cos((x/2^k ))))=(1/θ)sin((π/2)θ) θ=((1−((1/a))^n )/(a−1))](Q183670.png)
Commented by Vynho last updated on 28/Dec/22

Commented by mathlove last updated on 03/Jan/23

| ||
Question and Answers Forum | ||
Question Number 183320 by mathlove last updated on 25/Dec/22 | ||
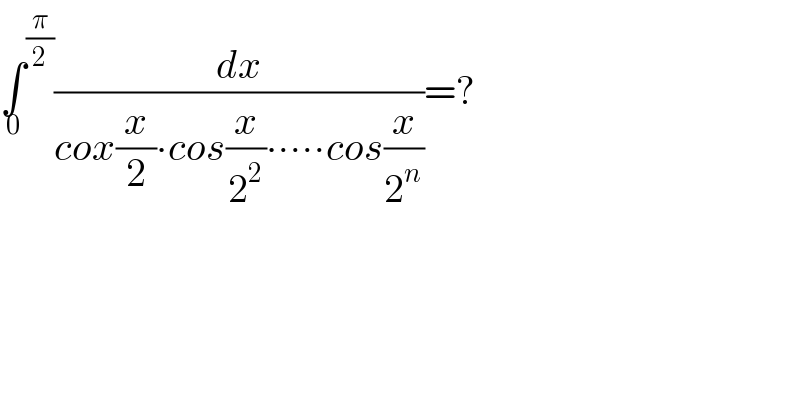 | ||
Answered by Vynho last updated on 28/Dec/22 | ||
![∫_0 ^(π/2) (dx/(Π_(k=1) ^n cos((x/2^k )))) ln(Π_(k=1) ^n cos((x/2^k )))=Σ_(k=1) ^n ln(cos((x/2^k ))) Π_(k=1) ^n cos((x/a^k ))+isin((x/a^k ))=Π_(k=1) ^n e^(i(x/a^k )) U_n =Π_(k=1) ^n e^(ix((1/a))^k ) ln(U_n )=Σ_(k=1) ^n ln(e^(ix((1/a))^k ) )=ixΣ_(k=1) ^n ((1/a))^k ln(U_n )=ix(1/a).((1−((1/a))^n )/(1−(1/a)))=ix.((1−((1/a))^n )/(a−1)) U_n =e^(ix((1−((1/a))^n )/(a−1))) ∫_0 ^(π/2) e^(−ix((1−((1/a))^n )/(a−1))) dx=∫_0 ^(π/2) e^(−ixθ) dx=(1/(−iθ))[e^(−ixθ) ]_0 ^(π/2) I=(i/θ)[e^(−i(π/2)θ) −1]=(1/θ)[icos((π/2)θ)+sin((π/2)θ)] ∫_0 ^(π/2) (dx/(Π_(k=1) ^n cos((x/2^k ))))=(1/θ)sin((π/2)θ) θ=((1−((1/a))^n )/(a−1))](Q183670.png) | ||
| ||
Commented by Vynho last updated on 28/Dec/22 | ||
 | ||
Commented by mathlove last updated on 03/Jan/23 | ||
 | ||