Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 183342 by Shrinava last updated on 25/Dec/22

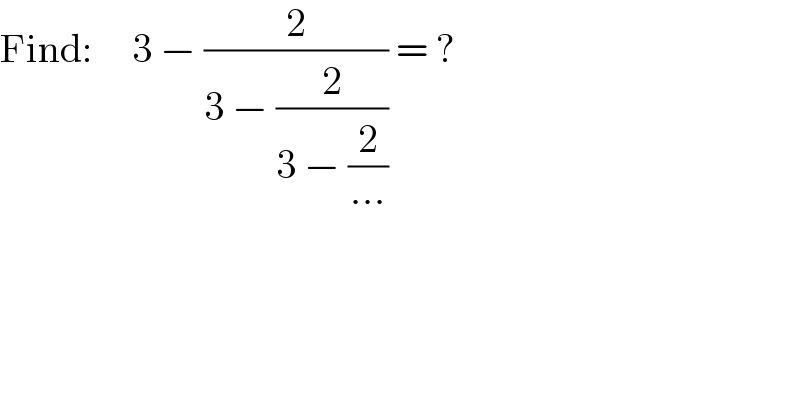
Find: 3 − (2/(3 − (2/(3 − (2/(...)))))) = ?

$$\mathrm{Find}:\:\:\:\:\:\mathrm{3}\:−\:\frac{\mathrm{2}}{\mathrm{3}\:−\:\frac{\mathrm{2}}{\mathrm{3}\:−\:\frac{\mathrm{2}}{...}}}\:=\:? \\ $$

Answered by Red1ight last updated on 25/Dec/22

3−(2/x)=x x^2 −3x+2=0 x=((3±(√(9−8)))/2) x=2,x=1

$$\mathrm{3}−\frac{\mathrm{2}}{{x}}={x} \\ $$$${x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{3}\pm\sqrt{\mathrm{9}−\mathrm{8}}}{\mathrm{2}} \\ $$$${x}=\mathrm{2},{x}=\mathrm{1} \\ $$

Commented by mr W last updated on 25/Dec/22

3−(2/(3−(2/(3−(2/(...))))))=1 3−(2/(3−(2/(3−(2/(...))))))=2 3−(2/(3−(2/(3−(2/(...))))))=3−(2/(3−(2/(3−(2/(...)))))) ⇒1=2 ?

$$\mathrm{3}−\frac{\mathrm{2}}{\mathrm{3}−\frac{\mathrm{2}}{\mathrm{3}−\frac{\mathrm{2}}{...}}}=\mathrm{1} \\ $$$$\mathrm{3}−\frac{\mathrm{2}}{\mathrm{3}−\frac{\mathrm{2}}{\mathrm{3}−\frac{\mathrm{2}}{...}}}=\mathrm{2} \\ $$$$\mathrm{3}−\frac{\mathrm{2}}{\mathrm{3}−\frac{\mathrm{2}}{\mathrm{3}−\frac{\mathrm{2}}{...}}}=\mathrm{3}−\frac{\mathrm{2}}{\mathrm{3}−\frac{\mathrm{2}}{\mathrm{3}−\frac{\mathrm{2}}{...}}} \\ $$$$\Rightarrow\mathrm{1}=\mathrm{2}\:? \\ $$

Answered by Frix last updated on 25/Dec/22

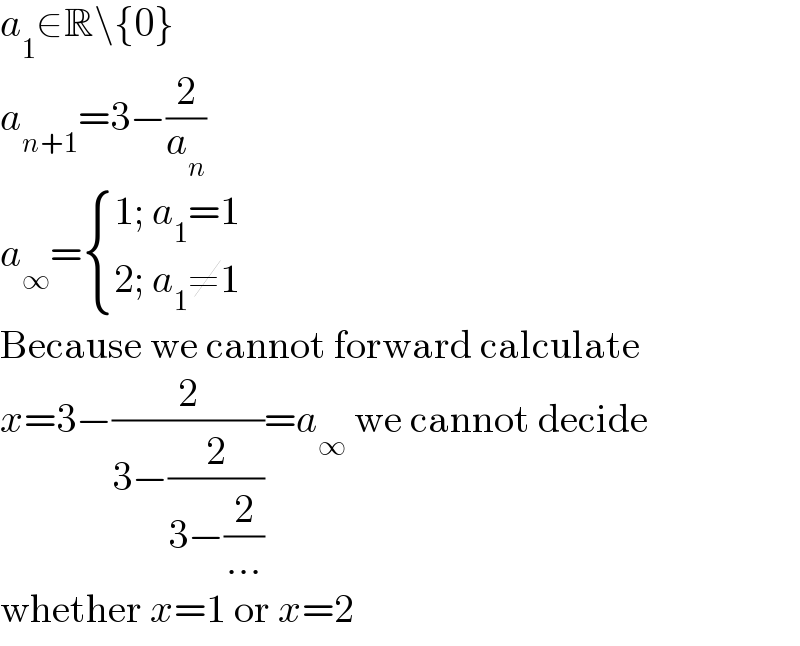
a_1 ∈R\{0} a_(n+1) =3−(2/a_n ) a_∞ = { ((1; a_1 =1)),((2; a_1 ≠1)) :} Because we cannot forward calculate x=3−(2/(3−(2/(3−(2/(...))))))=a_∞ we cannot decide whether x=1 or x=2

$${a}_{\mathrm{1}} \in\mathbb{R}\backslash\left\{\mathrm{0}\right\} \\ $$$${a}_{{n}+\mathrm{1}} =\mathrm{3}−\frac{\mathrm{2}}{{a}_{{n}} } \\ $$$${a}_{\infty} =\begin{cases}{\mathrm{1};\:{a}_{\mathrm{1}} =\mathrm{1}}\\{\mathrm{2};\:{a}_{\mathrm{1}} \neq\mathrm{1}}\end{cases} \\ $$$$\mathrm{Because}\:\mathrm{we}\:\mathrm{cannot}\:\mathrm{forward}\:\mathrm{calculate} \\ $$$${x}=\mathrm{3}−\frac{\mathrm{2}}{\mathrm{3}−\frac{\mathrm{2}}{\mathrm{3}−\frac{\mathrm{2}}{...}}}={a}_{\infty} \:\mathrm{we}\:\mathrm{cannot}\:\mathrm{decide} \\ $$$$\mathrm{whether}\:{x}=\mathrm{1}\:\mathrm{or}\:{x}=\mathrm{2} \\ $$

Commented by Shrinava last updated on 25/Dec/22

Answer: 2

$$\mathrm{Answer}:\:\mathrm{2} \\ $$

Commented by Frix last updated on 25/Dec/22

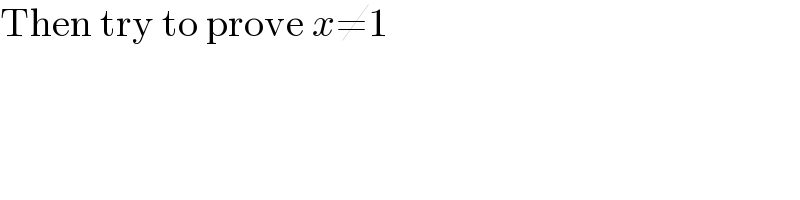
Then try to prove x≠1

$$\mathrm{Then}\:\mathrm{try}\:\mathrm{to}\:\mathrm{prove}\:{x}\neq\mathrm{1} \\ $$

Answered by mahdipoor last updated on 25/Dec/22

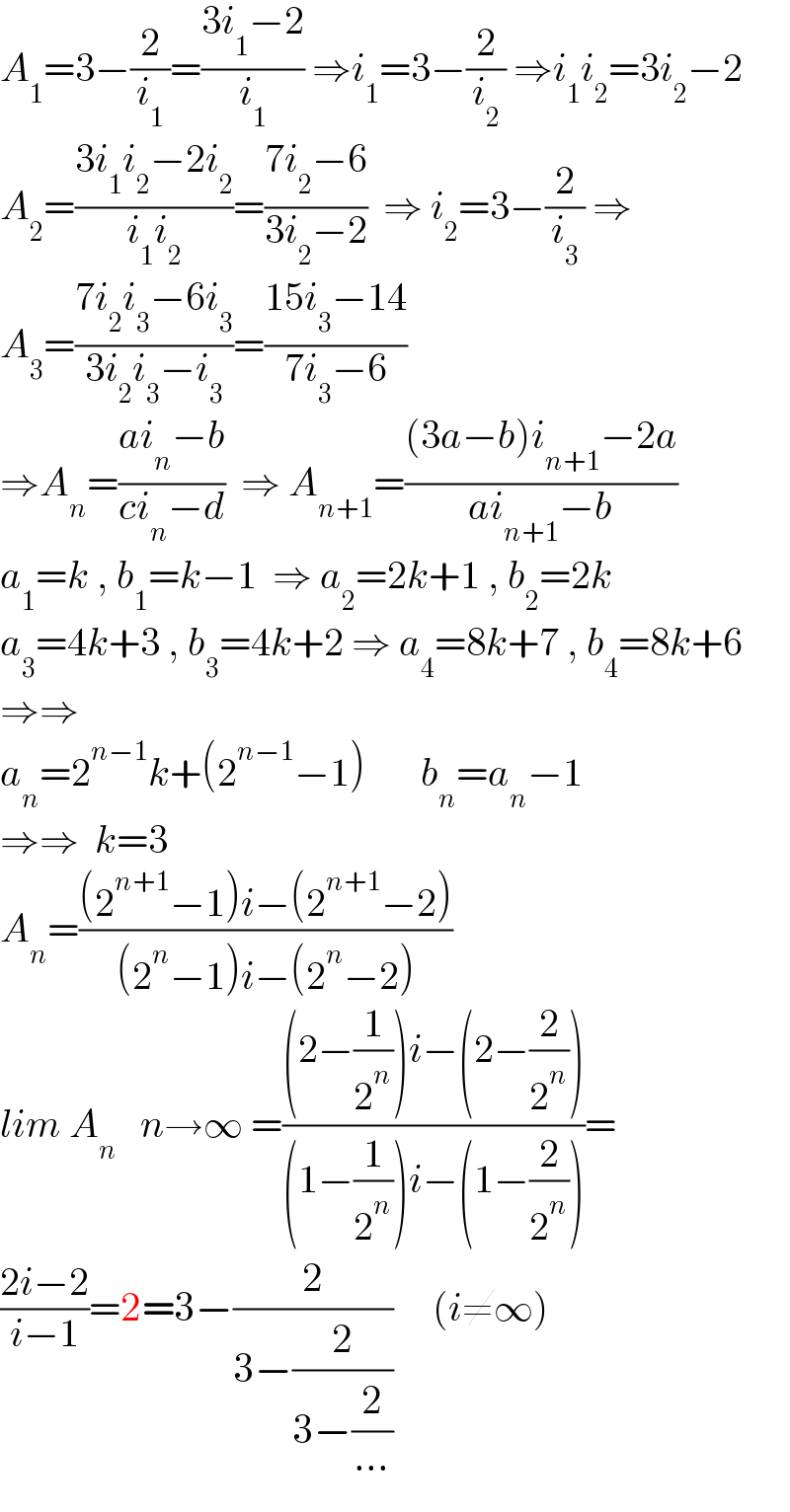
A_1 =3−(2/i_1 )=((3i_1 −2)/i_1 ) ⇒i_1 =3−(2/i_2 ) ⇒i_1 i_2 =3i_2 −2 A_2 =((3i_1 i_2 −2i_2 )/(i_1 i_2 ))=((7i_2 −6)/(3i_2 −2)) ⇒ i_2 =3−(2/i_3 ) ⇒ A_3 =((7i_2 i_3 −6i_3 )/(3i_2 i_3 −i_3 ))=((15i_3 −14)/(7i_3 −6)) ⇒A_n =((ai_n −b)/(ci_n −d)) ⇒ A_(n+1) =(((3a−b)i_(n+1) −2a)/(ai_(n+1) −b)) a_1 =k , b_1 =k−1 ⇒ a_2 =2k+1 , b_2 =2k a_3 =4k+3 , b_3 =4k+2 ⇒ a_4 =8k+7 , b_4 =8k+6 ⇒⇒ a_n =2^(n−1) k+(2^(n−1) −1) b_n =a_n −1 ⇒⇒ k=3 A_n =(((2^(n+1) −1)i−(2^(n+1) −2))/((2^n −1)i−(2^n −2))) lim A_n n→∞ =(((2−(1/2^n ))i−(2−(2/2^n )))/((1−(1/2^n ))i−(1−(2/2^n ))))= ((2i−2)/(i−1))=2=3−(2/(3−(2/(3−(2/(...)))))) (i≠∞)

$${A}_{\mathrm{1}} =\mathrm{3}−\frac{\mathrm{2}}{{i}_{\mathrm{1}} }=\frac{\mathrm{3}{i}_{\mathrm{1}} −\mathrm{2}}{{i}_{\mathrm{1}} }\:\Rightarrow{i}_{\mathrm{1}} =\mathrm{3}−\frac{\mathrm{2}}{{i}_{\mathrm{2}} }\:\Rightarrow{i}_{\mathrm{1}} {i}_{\mathrm{2}} =\mathrm{3}{i}_{\mathrm{2}} −\mathrm{2} \\ $$$${A}_{\mathrm{2}} =\frac{\mathrm{3}{i}_{\mathrm{1}} {i}_{\mathrm{2}} −\mathrm{2}{i}_{\mathrm{2}} }{{i}_{\mathrm{1}} {i}_{\mathrm{2}} }=\frac{\mathrm{7}{i}_{\mathrm{2}} −\mathrm{6}}{\mathrm{3}{i}_{\mathrm{2}} −\mathrm{2}}\:\:\Rightarrow\:{i}_{\mathrm{2}} =\mathrm{3}−\frac{\mathrm{2}}{{i}_{\mathrm{3}} }\:\Rightarrow \\ $$$${A}_{\mathrm{3}} =\frac{\mathrm{7}{i}_{\mathrm{2}} {i}_{\mathrm{3}} −\mathrm{6}{i}_{\mathrm{3}} }{\mathrm{3}{i}_{\mathrm{2}} {i}_{\mathrm{3}} −{i}_{\mathrm{3}} }=\frac{\mathrm{15}{i}_{\mathrm{3}} −\mathrm{14}}{\mathrm{7}{i}_{\mathrm{3}} −\mathrm{6}} \\ $$$$\Rightarrow{A}_{{n}} =\frac{{ai}_{{n}} −{b}}{{ci}_{{n}} −{d}}\:\:\Rightarrow\:{A}_{{n}+\mathrm{1}} =\frac{\left(\mathrm{3}{a}−{b}\right){i}_{{n}+\mathrm{1}} −\mathrm{2}{a}}{{ai}_{{n}+\mathrm{1}} −{b}} \\ $$$${a}_{\mathrm{1}} ={k}\:,\:{b}_{\mathrm{1}} ={k}−\mathrm{1}\:\:\Rightarrow\:{a}_{\mathrm{2}} =\mathrm{2}{k}+\mathrm{1}\:,\:{b}_{\mathrm{2}} =\mathrm{2}{k} \\ $$$${a}_{\mathrm{3}} =\mathrm{4}{k}+\mathrm{3}\:,\:{b}_{\mathrm{3}} =\mathrm{4}{k}+\mathrm{2}\:\Rightarrow\:{a}_{\mathrm{4}} =\mathrm{8}{k}+\mathrm{7}\:,\:{b}_{\mathrm{4}} =\mathrm{8}{k}+\mathrm{6}\: \\ $$$$\Rightarrow\Rightarrow \\ $$$${a}_{{n}} =\mathrm{2}^{{n}−\mathrm{1}} {k}+\left(\mathrm{2}^{{n}−\mathrm{1}} −\mathrm{1}\right)\:\:\:\:\:\:\:{b}_{{n}} ={a}_{{n}} −\mathrm{1} \\ $$$$\Rightarrow\Rightarrow\:\:{k}=\mathrm{3} \\ $$$${A}_{{n}} =\frac{\left(\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}\right){i}−\left(\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{2}\right)}{\left(\mathrm{2}^{{n}} −\mathrm{1}\right){i}−\left(\mathrm{2}^{{n}} −\mathrm{2}\right)} \\ $$$${lim}\:{A}_{{n}} \:\:\:{n}\rightarrow\infty\:=\frac{\left(\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right){i}−\left(\mathrm{2}−\frac{\mathrm{2}}{\mathrm{2}^{{n}} }\right)}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right){i}−\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{2}^{{n}} }\right)}= \\ $$$$\frac{\mathrm{2}{i}−\mathrm{2}}{{i}−\mathrm{1}}=\mathrm{2}=\mathrm{3}−\frac{\mathrm{2}}{\mathrm{3}−\frac{\mathrm{2}}{\mathrm{3}−\frac{\mathrm{2}}{...}}}\:\:\:\:\:\left({i}\neq\infty\right) \\ $$

Commented by Frix last updated on 25/Dec/22

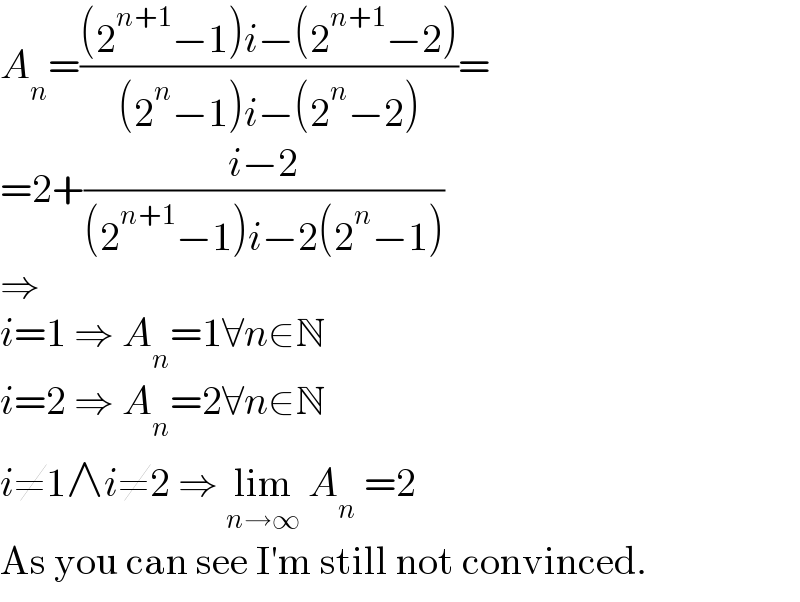
A_n =(((2^(n+1) −1)i−(2^(n+1) −2))/((2^n −1)i−(2^n −2)))= =2+((i−2)/((2^(n+1) −1)i−2(2^n −1))) ⇒ i=1 ⇒ A_n =1∀n∈N i=2 ⇒ A_n =2∀n∈N i≠1∧i≠2 ⇒ lim_(n→∞) A_n =2 As you can see I′m still not convinced.

$${A}_{{n}} =\frac{\left(\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}\right){i}−\left(\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{2}\right)}{\left(\mathrm{2}^{{n}} −\mathrm{1}\right){i}−\left(\mathrm{2}^{{n}} −\mathrm{2}\right)}= \\ $$$$=\mathrm{2}+\frac{{i}−\mathrm{2}}{\left(\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}\right){i}−\mathrm{2}\left(\mathrm{2}^{{n}} −\mathrm{1}\right)} \\ $$$$\Rightarrow \\ $$$${i}=\mathrm{1}\:\Rightarrow\:{A}_{{n}} =\mathrm{1}\forall{n}\in\mathbb{N} \\ $$$${i}=\mathrm{2}\:\Rightarrow\:{A}_{{n}} =\mathrm{2}\forall{n}\in\mathbb{N} \\ $$$${i}\neq\mathrm{1}\wedge{i}\neq\mathrm{2}\:\Rightarrow\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{A}_{{n}} \:=\mathrm{2} \\ $$$$\mathrm{As}\:\mathrm{you}\:\mathrm{can}\:\mathrm{see}\:\mathrm{I}'\mathrm{m}\:\mathrm{still}\:\mathrm{not}\:\mathrm{convinced}. \\ $$

Commented by Frix last updated on 25/Dec/22

I don′t think numbers of the shape x=m+(n/(m+(n/(m+(n/(...)))))) with m, n ∈Z can generally be given a value. We can always solve for x∈C: x=m+(n/x) ⇒ x=((m±(√(m^2 +4n)))/2) But how to prove the value of this example? x=3−(3/(3−(3/(3−(3/(...))))))=^(???) (3/2)±((√3)/2)i You tell me adding, substracting, dividing by real numbers gives complex numbers?

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{numbers}\:\mathrm{of}\:\mathrm{the}\:\mathrm{shape} \\ $$$${x}={m}+\frac{{n}}{{m}+\frac{{n}}{{m}+\frac{{n}}{...}}}\:\mathrm{with}\:{m},\:{n}\:\in\mathbb{Z} \\ $$$$\mathrm{can}\:\mathrm{generally}\:\mathrm{be}\:\mathrm{given}\:\mathrm{a}\:\mathrm{value}.\:\mathrm{We}\:\mathrm{can} \\ $$$$\mathrm{always}\:\mathrm{solve}\:\mathrm{for}\:{x}\in\mathbb{C}: \\ $$$${x}={m}+\frac{{n}}{{x}}\:\Rightarrow\:{x}=\frac{{m}\pm\sqrt{{m}^{\mathrm{2}} +\mathrm{4}{n}}}{\mathrm{2}} \\ $$$$\mathrm{But}\:\mathrm{how}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{this}\:\mathrm{example}? \\ $$$${x}=\mathrm{3}−\frac{\mathrm{3}}{\mathrm{3}−\frac{\mathrm{3}}{\mathrm{3}−\frac{\mathrm{3}}{...}}}\overset{???} {=}\frac{\mathrm{3}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i} \\ $$$$\mathrm{You}\:\mathrm{tell}\:\mathrm{me}\:\mathrm{adding},\:\mathrm{substracting},\:\mathrm{dividing} \\ $$$$\mathrm{by}\:\mathrm{real}\:\mathrm{numbers}\:\mathrm{gives}\:\mathrm{complex}\:\mathrm{numbers}? \\ $$

Commented by mahdipoor last updated on 26/Dec/22

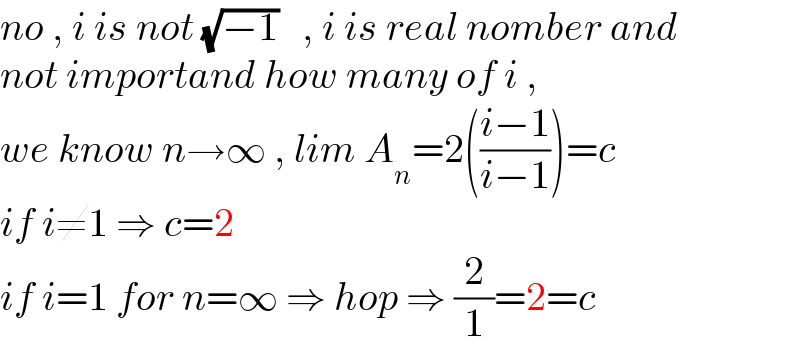
no , i is not (√(−1)) , i is real nomber and not importand how many of i , we know n→∞ , lim A_n =2(((i−1)/(i−1)))=c if i≠1 ⇒ c=2 if i=1 for n=∞ ⇒ hop ⇒ (2/1)=2=c

$${no}\:,\:{i}\:{is}\:{not}\:\sqrt{−\mathrm{1}}\:\:\:,\:{i}\:{is}\:{real}\:{nomber}\:{and}\: \\ $$$${not}\:{importand}\:{how}\:{many}\:{of}\:{i}\:, \\ $$$${we}\:{know}\:{n}\rightarrow\infty\:,\:{lim}\:{A}_{{n}} =\mathrm{2}\left(\frac{{i}−\mathrm{1}}{{i}−\mathrm{1}}\right)={c}\: \\ $$$${if}\:{i}\neq\mathrm{1}\:\Rightarrow\:{c}=\mathrm{2} \\ $$$${if}\:{i}=\mathrm{1}\:{for}\:{n}=\infty\:\Rightarrow\:{hop}\:\Rightarrow\:\frac{\mathrm{2}}{\mathrm{1}}=\mathrm{2}={c} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com