Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 183485 by Gamil last updated on 26/Dec/22

$$\mathbf{L}=\underset{x\to 0}{\lim }\frac{2\mathbf{sin}\mathbf{x}-2\mathbf{tan}\mathbf{x}+{\mathbf{x}}^3}{6\mathbf{x}-2\mathbf{sin}3\mathbf{x}-9{\mathbf{x}}^3}$$$$\mathbf{L}=\frac{\underset{x\to 0}{\lim }\frac{2\mathbf{sin}\mathbf{x}-2\mathbf{tan}\mathbf{x}+{\mathbf{x}}^3}{{\mathbf{x}}^5}}{\underset{x\to 0}{\lim }\frac{6\mathbf{x}-2\mathbf{sin}3\mathbf{x}-9{\mathbf{x}}^3}{{\mathbf{x}}^5}}=\frac{{\mathbf{L}}_1}{{\mathbf{L}}_2}$$

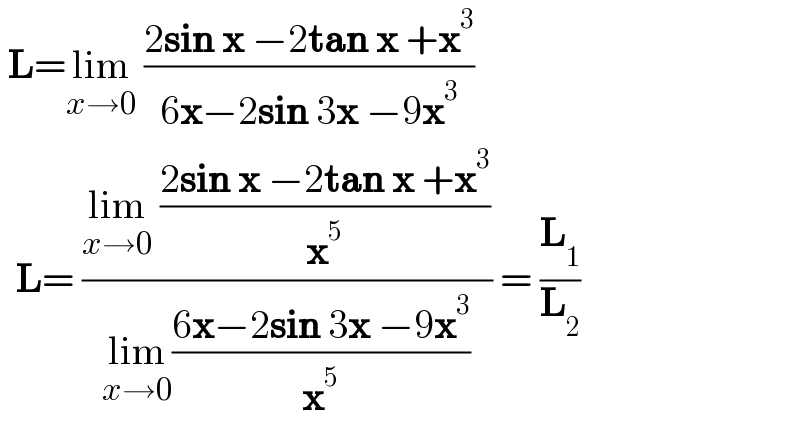
Commented by CElcedricjunior last updated on 26/Dec/22

$$\mathbf{l}=\underset{x\to 0}{\lim }\frac{2\mathbf{sinx}-2\mathbf{tanx}+{\mathbf{x}}^3}{6\mathbf{x}-2\mathbf{sin}3\mathbf{x}-9{\mathbf{x}}^3}=\frac{0}{0}=\mathbf{fi}$$$$\mathbf{to}\mathbf{apply}\mathbf{hospital}$$$$\underset{x\to 0}{\lim }\frac{2\mathbf{cosx}-2(1+\mathbf{ta}\stackrel{2}{\mathbf{n}\mathit{x}})+3{\mathbf{x}}^2}{6-6\mathbf{cos}3\mathbf{x}-27{\mathbf{x}}^2}=\frac{0}{0}=\mathbf{fi}$$$$\underset{x\to 0}{\lim }\frac{-2\mathbf{sinx}-4\mathbf{tanx}(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})+6\mathit{x}}{18\mathit{s}\mathit{i}\mathit{n}3\mathit{x}-54\mathit{x}}=\frac{0}{0}=\mathit{f}\mathit{i}$$$$\underset{x\to 0}{\lim }\frac{-2\mathit{c}\mathit{o}\mathit{s}\mathit{x}-4{(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})}^2-8\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}}(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})+6}{54\mathit{c}\mathit{o}\mathit{s}3\mathit{x}-54}=\frac{0}{0}=\mathit{f}\mathit{i}$$$$\underset{x\to 0}{\lim }\frac{2\mathit{s}\mathit{i}\mathit{n}\mathit{x}-8\mathit{t}\mathit{a}\mathit{n}\mathit{x}{(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})}^3-16\mathit{t}\mathit{a}\mathit{n}\mathit{x}{(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})}^2-16\mathit{t}\mathit{a}\stackrel{3}{\mathit{n}\mathit{x}}(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})}{-162\mathit{s}\mathit{i}\mathit{n}3\mathit{x}}$$$$\underset{x\to 0}{\lim }\frac{\frac{2}{1}\times \frac{\mathit{s}\mathit{i}\mathit{n}\mathit{x}}{\mathit{x}}-8\frac{\mathit{t}\mathit{a}\mathit{n}\mathit{x}}{\mathit{x}}\times {(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})}^3-16\frac{\mathit{t}\mathit{a}\mathit{n}\mathit{x}}{\mathit{x}}(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})-\frac{16\mathit{t}\mathit{a}\stackrel{3}{\mathit{n}}}{\mathit{x}}\times (1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})}{-486\frac{\mathit{s}\mathit{i}\mathit{n}3\mathit{x}}{3\mathit{x}}}$$$$\mathit{l}=\frac{2-8-16+0}{-486}=\frac{22}{486}=\frac{11}{243}$$$$\left(2\right)$$$$$$$$$$

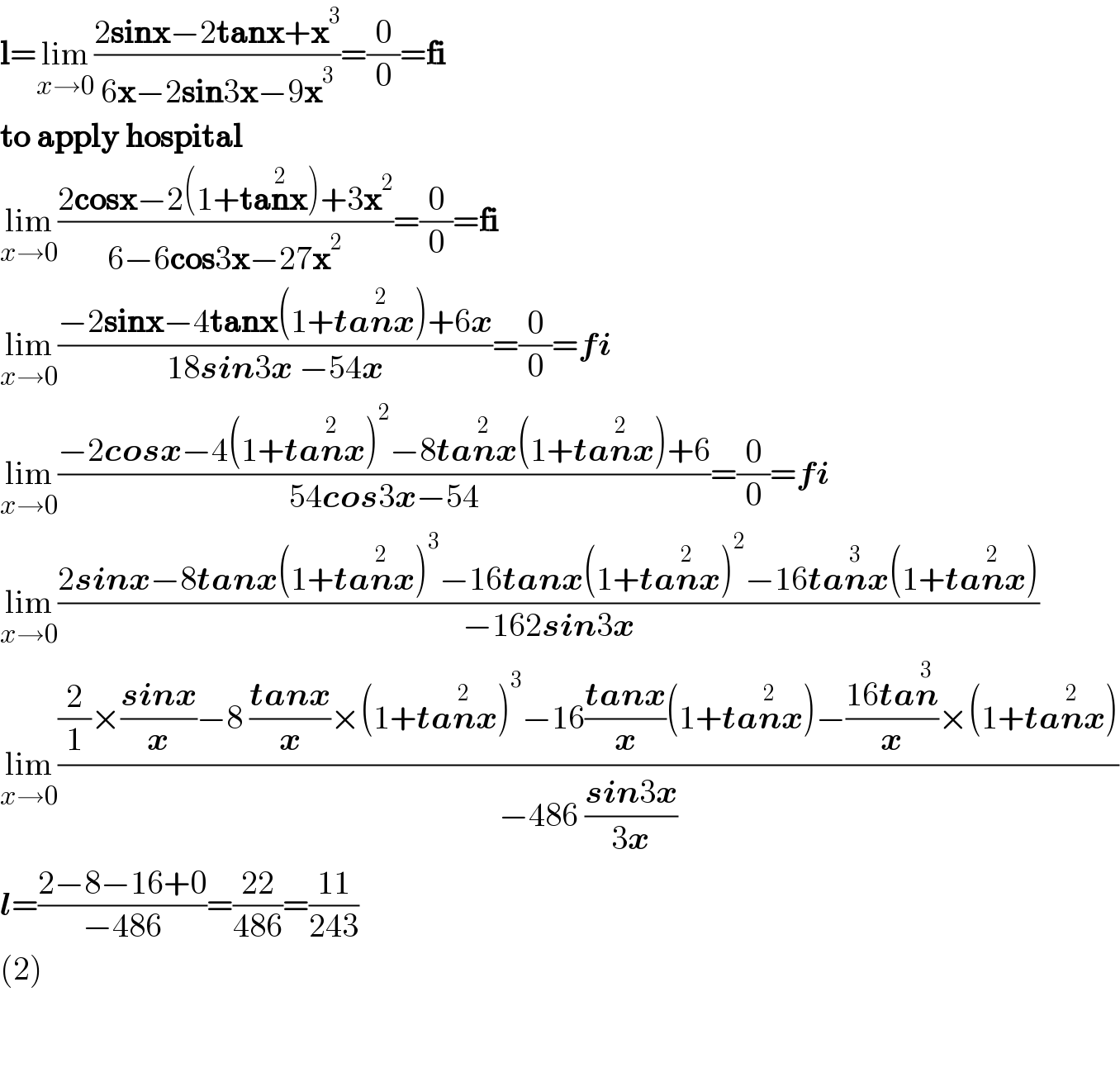
Answered by CElcedricjunior last updated on 26/Dec/22

$$\mathit{l}=\frac{\underset{x\to 0}{\lim }\frac{2\mathit{s}\mathit{i}\mathit{n}\mathit{x}-2\mathit{t}\mathit{a}\mathit{n}\mathit{x}+{\mathit{x}}^3}{{\mathit{x}}^5}}{\underset{x\to 0}{\lim }\frac{6\mathit{x}-2\mathit{s}\mathit{i}\mathit{n}3\mathit{x}-9{\mathit{x}}^3}{{\mathit{x}}^5}}$$$$=\underset{x\to 0}{\lim }\frac{2\mathit{s}\mathit{i}\mathit{n}\mathit{x}-2\mathit{t}\mathit{a}\mathit{n}\mathit{x}+{\mathit{x}}^3}{6\mathit{x}-2\mathit{s}\mathit{i}\mathit{n}3\mathit{x}-9{\mathit{x}}^3}=\frac{0}{0}\mathit{f}\mathit{i}$$$$\mathit{t}\mathit{o}\mathit{a}\mathit{p}\mathit{p}\mathit{l}\mathit{y}\mathit{h}\mathit{o}\mathit{s}\mathit{p}\mathit{i}\mathit{t}\mathit{a}\mathit{l}$$$$=\underset{x\to 0}{\lim }\frac{2\mathit{c}\mathit{o}\mathit{s}\mathit{x}-2(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})+3{\mathit{x}}^2}{6-6\mathit{c}\mathit{o}\mathit{s}3\mathit{x}-27\stackrel{2}{\mathit{x}}}=\frac{0}{0}\mathit{f}\mathit{i}$$$$=\underset{x\to 0}{\lim }\frac{-2\mathit{s}\mathit{i}\mathit{n}\mathit{x}-4\mathit{t}\mathit{a}\mathit{n}\mathit{x}(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})+6\mathit{x}}{+18\mathit{s}\mathit{i}\mathit{n}3\mathit{x}-54\mathit{x}}=\frac{0}{0}\mathit{f}\mathit{i}$$$$=\underset{x\to 0}{\lim }\frac{-2\mathit{c}\mathit{o}\mathit{s}\mathit{x}-4{(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})}^2-8\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}}(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})+6}{54\mathit{c}\mathit{o}\mathit{s}3\mathit{x}-54}=\frac{0}{0}=\mathit{f}\mathit{i}$$$$=\underset{x\to 0}{\lim }\frac{2\mathit{s}\mathit{i}\mathit{n}\mathit{x}-8\mathit{t}\mathit{a}\mathit{n}\mathit{x}{(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})}^2-16\mathit{t}\mathit{a}\mathit{n}{(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})}^2-16\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}}(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})}{-164\mathit{s}\mathit{i}\mathit{n}3\mathit{x}}$$$$=\underset{x\to 0}{\lim }\frac{2\frac{\mathit{s}\mathit{i}\mathit{n}\mathit{x}}{\mathit{x}}-8\frac{\mathit{t}\mathit{a}\mathit{n}\mathit{x}}{\mathit{x}}(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})-16\frac{\mathit{t}\mathit{a}\mathit{n}\mathit{x}}{\mathit{x}}{(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})}^2-16\frac{\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}}}{\mathit{x}}(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})}{-492\frac{\mathit{s}\mathit{i}\mathit{n}3\mathit{x}}{3\mathit{x}}}$$$$\mathit{l}=\frac{2-8-16}{-492}=\frac{22}{492}=\frac{11}{246}$$$$\mathit{l}=\frac{\underset{x\to 0}{\lim }\frac{2\mathit{s}\mathit{i}\mathit{n}\mathit{x}-2\mathit{t}\mathit{a}\mathit{n}\mathit{x}+{\mathit{x}}^3}{{\mathit{x}}^5}}{\underset{x\to 0}{\lim }\frac{6\mathit{x}-2\mathit{s}\mathit{i}\mathit{n}3\mathit{x}-9{\mathit{x}}^3}{{\mathit{x}}^5}}$$$$=\underset{x\to 0}{\lim }\frac{2\mathit{s}\mathit{i}\mathit{n}\mathit{x}-2\mathit{t}\mathit{a}\mathit{n}\mathit{x}+{\mathit{x}}^3}{6\mathit{x}-2\mathit{s}\mathit{i}\mathit{n}3\mathit{x}-9{\mathit{x}}^3}=\frac{0}{0}\mathit{f}\mathit{i}$$$$\mathit{t}\mathit{o}\mathit{a}\mathit{p}\mathit{p}\mathit{l}\mathit{y}\mathit{h}\mathit{o}\mathit{s}\mathit{p}\mathit{i}\mathit{t}\mathit{a}\mathit{l}$$$$=\underset{x\to 0}{\lim }\frac{2\mathit{c}\mathit{o}\mathit{s}\mathit{x}-2(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})+3{\mathit{x}}^2}{6-6\mathit{c}\mathit{o}\mathit{s}3\mathit{x}-27\stackrel{2}{\mathit{x}}}=\frac{0}{0}\mathit{f}\mathit{i}$$$$=\underset{x\to 0}{\lim }\frac{-2\mathit{s}\mathit{i}\mathit{n}\mathit{x}-4\mathit{t}\mathit{a}\mathit{n}\mathit{x}(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})+6\mathit{x}}{+18\mathit{s}\mathit{i}\mathit{n}3\mathit{x}-54\mathit{x}}=\frac{0}{0}\mathit{f}\mathit{i}$$$$=\underset{x\to 0}{\lim }\frac{-2\mathit{c}\mathit{o}\mathit{s}\mathit{x}-4{(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})}^2-8\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}}(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})+6}{54\mathit{c}\mathit{o}\mathit{s}3\mathit{x}-54}=\frac{0}{0}=\mathit{f}\mathit{i}$$$$=\underset{x\to 0}{\lim }\frac{2\mathit{s}\mathit{i}\mathit{n}\mathit{x}-8\mathit{t}\mathit{a}\mathit{n}\mathit{x}{(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})}^2-16\mathit{t}\mathit{a}\mathit{n}{(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})}^2-16\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}}(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})}{-164\mathit{s}\mathit{i}\mathit{n}3\mathit{x}}$$$$=\underset{x\to 0}{\lim }\frac{2\frac{\mathit{s}\mathit{i}\mathit{n}\mathit{x}}{\mathit{x}}-8\frac{\mathit{t}\mathit{a}\mathit{n}\mathit{x}}{\mathit{x}}(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})-16\frac{\mathit{t}\mathit{a}\mathit{n}\mathit{x}}{\mathit{x}}{(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})}^2-16\frac{\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}}}{\mathit{x}}(1+\mathit{t}\mathit{a}\stackrel{2}{\mathit{n}\mathit{x}})}{-492\frac{\mathit{s}\mathit{i}\mathit{n}3\mathit{x}}{3\mathit{x}}}$$$$\mathit{l}=\frac{2-8-16}{-492}=\frac{22}{492}=\frac{11}{246}$$$$$$$$\mathrm{l}>$$$$$$$$\mathrm{l}>$$

Commented by Ar Brandon last updated on 26/Dec/22

C'est mieux ainsi ������

Answered by Ar Brandon last updated on 26/Dec/22

$$\mathcal{L}=\underset{x\to 0}{\lim }\frac{2\sin x-2\tan x+x^3}{6x-2\sin 3x-9x^3}$$$$[\sin x\to x-\frac{x^3}{3!}+\frac{x^5}{5!}:\tan x\to x+\frac{x^3}{3}+\frac{2x^5}{15}]$$$$=\underset{x\to 0}{\lim }\frac{2(x-\frac{x^3}{6}+\frac{x^5}{120})-2(x+\frac{x^3}{3}+\frac{2x^5}{15})+x^3}{6x-2(3x-\frac{27x^3}{6}+\frac{243x^5}{120})-9x^3}$$$$=\underset{x\to 0}{\lim }\frac{-\frac{1}{4}{x}^5}{-\frac{243}{60}{x}^5}=\frac{5}{81}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com