
Question and Answers Forum
Question Number 183559 by cortano1 last updated on 27/Dec/22
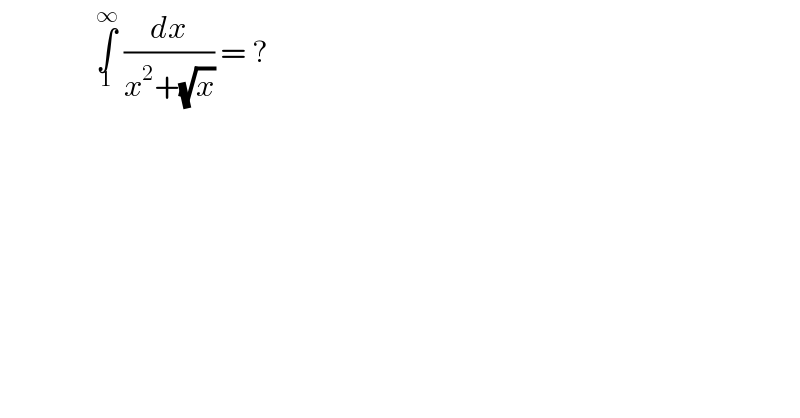
Answered by greougoury555 last updated on 27/Dec/22
![G = ∫_1 ^( ∞) (dx/(x^2 +(√x))) = ∫_1 ^( ∞) ((2du)/(u^3 +1)) = (1/3) [ ∫_1 ^( ∞) ( (2/(u+1))−((2u−4)/(u^2 −u+1))) du ] = (1/3) [ 2ln ∣u+1∣−∫_1 ^( ∞) ((2(u−(1/2))−3)/((u−(1/2))^2 +(3/4))) du ] = (1/3) [ 2ln ∣u+1∣ −ln ((u−(1/2))^2 +(3/4))+2(√3) tan^(−1) (((2(u−(1/2)))/( (√3)))) ]_1 ^∞ = (1/3) [ ln ∣(((u+1)^2 )/(u^2 −u+1))∣+2(√3) tan^(−1) (((2u−1)/( (√3))))]_1 ^∞ = ((2π)/(3(√3)))−ln (4)^(1/3) = ((2π(√3))/9) −ln (4)^(1/3)](Q183597.png)
| ||
Question and Answers Forum | ||
Question Number 183559 by cortano1 last updated on 27/Dec/22 | ||
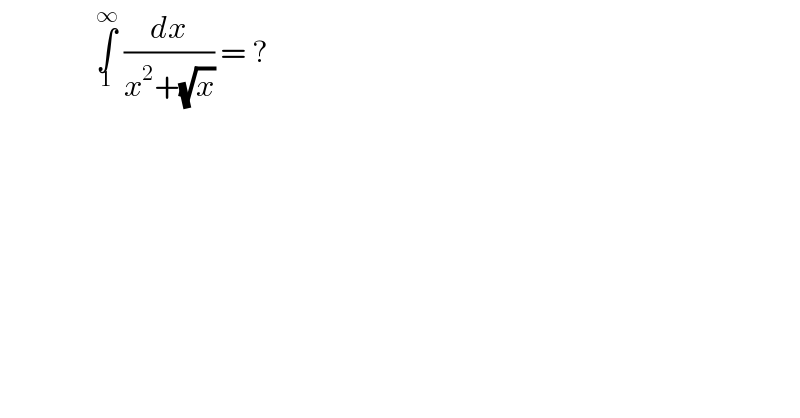 | ||
Answered by greougoury555 last updated on 27/Dec/22 | ||
![G = ∫_1 ^( ∞) (dx/(x^2 +(√x))) = ∫_1 ^( ∞) ((2du)/(u^3 +1)) = (1/3) [ ∫_1 ^( ∞) ( (2/(u+1))−((2u−4)/(u^2 −u+1))) du ] = (1/3) [ 2ln ∣u+1∣−∫_1 ^( ∞) ((2(u−(1/2))−3)/((u−(1/2))^2 +(3/4))) du ] = (1/3) [ 2ln ∣u+1∣ −ln ((u−(1/2))^2 +(3/4))+2(√3) tan^(−1) (((2(u−(1/2)))/( (√3)))) ]_1 ^∞ = (1/3) [ ln ∣(((u+1)^2 )/(u^2 −u+1))∣+2(√3) tan^(−1) (((2u−1)/( (√3))))]_1 ^∞ = ((2π)/(3(√3)))−ln (4)^(1/3) = ((2π(√3))/9) −ln (4)^(1/3)](Q183597.png) | ||
| ||