
Question and Answers Forum
Question Number 183927 by greougoury555 last updated on 31/Dec/22
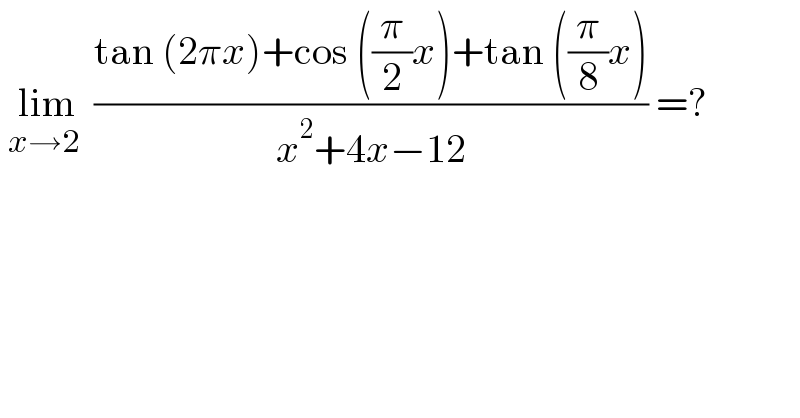
Answered by cortano1 last updated on 31/Dec/22
![lim_(x→2) ((tan (2πx)+cos ((π/2)x)+tan ((π/8)x))/((x−2)(x+6))) = lim_(x→2) ((tan (2πx)+cos ((π/2)x)+tan ((π/8)x))/(8(x−2))) [ x−2=m ] = lim_(m→0) ((tan (2π(m+2))+cos ((π/2)(m+2))+tan ((π/8)(m+2)))/(8m)) =lim_(m→0) ((tan (2πm)−cos ((π/2)m)+tan ((π/8)m+(π/4)))/(8m)) =(π/4)+lim_(m→0) ((1−cos ((π/2)m))/(8m)) +lim_(m→0) ((tan ((π/8)m+(π/4))−tan (π/4))/(8m)) =(π/4)+lim_(m→0) ((sin^2 ((π/2)m))/(16m)) +lim_(m→0) ((tan ((π/8)m)[ 1+tan ((π/8)m+(π/4))])/(8m)) =(π/4)+0+((2.π)/(64)) = ((9π)/(32))](Q183928.png)
Answered by qaz last updated on 31/Dec/22
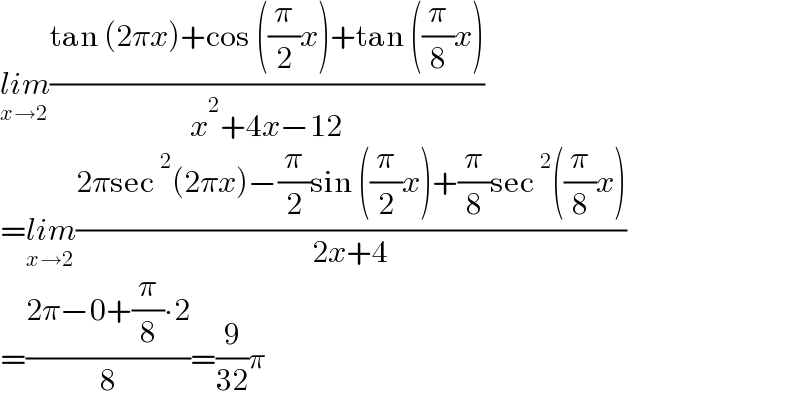
| ||
Question and Answers Forum | ||
Question Number 183927 by greougoury555 last updated on 31/Dec/22 | ||
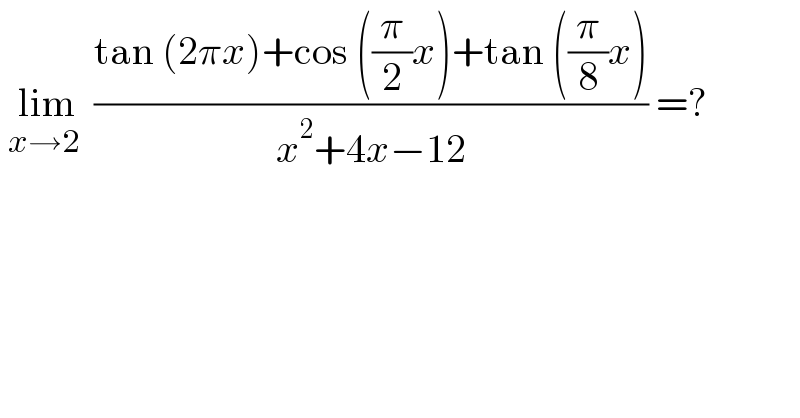 | ||
Answered by cortano1 last updated on 31/Dec/22 | ||
![lim_(x→2) ((tan (2πx)+cos ((π/2)x)+tan ((π/8)x))/((x−2)(x+6))) = lim_(x→2) ((tan (2πx)+cos ((π/2)x)+tan ((π/8)x))/(8(x−2))) [ x−2=m ] = lim_(m→0) ((tan (2π(m+2))+cos ((π/2)(m+2))+tan ((π/8)(m+2)))/(8m)) =lim_(m→0) ((tan (2πm)−cos ((π/2)m)+tan ((π/8)m+(π/4)))/(8m)) =(π/4)+lim_(m→0) ((1−cos ((π/2)m))/(8m)) +lim_(m→0) ((tan ((π/8)m+(π/4))−tan (π/4))/(8m)) =(π/4)+lim_(m→0) ((sin^2 ((π/2)m))/(16m)) +lim_(m→0) ((tan ((π/8)m)[ 1+tan ((π/8)m+(π/4))])/(8m)) =(π/4)+0+((2.π)/(64)) = ((9π)/(32))](Q183928.png) | ||
| ||
Answered by qaz last updated on 31/Dec/22 | ||
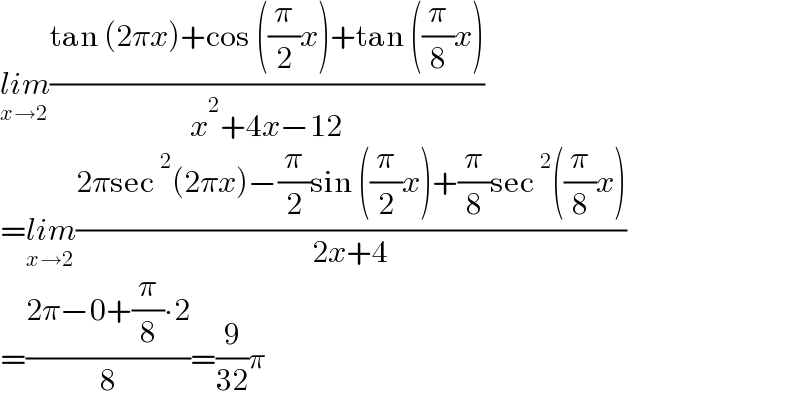 | ||
| ||