Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 183977 by cortano1 last updated on 01/Jan/23

$${\int }_0^{\mathrm{\infty }}\frac{dx}{x^8+x^4+1}=?$$

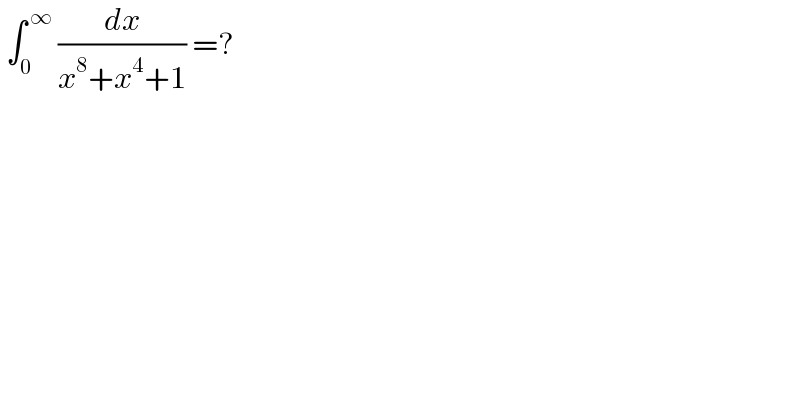
Answered by ARUNG_Brandon_MBU last updated on 01/Jan/23

$$\mathrm{\Omega }={\int }_0^{\mathrm{\infty }}\frac{dx}{x^8+x^4+1}={\int }_0^{\mathrm{\infty }}\frac{1-x^4}{1-x^{12}}dx={\int }_0^1\frac{1-x^4}{1-x^{12}}dx+{\int }_1^{\mathrm{\infty }}\frac{1-x^4}{1-x^{12}}dx$$$$={\int }_0^1\frac{1-x^4}{1-x^{12}}dx+{\int }_0^1\frac{1-\frac{1}{x^4}}{1-\frac{1}{x^{12}}}\cdot \frac{1}{x^2}dx={\int }_0^1\frac{1-x^4}{1-x^{12}}dx+{\int }_0^1\frac{x^{10}-x^6}{x^{12}-1}dx$$$$={\int }_0^1\frac{1-x^4+x^6-x^{10}}{1-x^{12}}dx=\frac{1}{12}{\int }_0^1\frac{x^{-\frac{11}{12}}-x^{-\frac{7}{12}}+x^{-\frac{5}{12}}-x^{-\frac{1}{12}}}{1-x}dx$$$$=\frac{1}{12}(\psi \left(\frac{11}{12}\right)-\psi \left(\frac{1}{12}\right)+\psi \left(\frac{5}{12}\right)-\psi \left(\frac{7}{12}\right))=\frac{1}{12}(\pi \cot \left(\frac{\pi }{12}\right)-\pi \cot \left(\frac{5\pi }{12}\right))$$$$=\frac{\pi }{12}(\frac{\sqrt{6}+\sqrt{2}}{\sqrt{6}-\sqrt{2}}-\frac{\sqrt{6}-\sqrt{2}}{\sqrt{6}+\sqrt{2}})=\frac{\pi }{12}\left(\frac{(8+4\sqrt{3})-(8-4\sqrt{3})}{4}\right)=\frac{\pi \sqrt{3}}{6}$$

Commented by MJS_new last updated on 01/Jan/23

$$\mathrm{great}!$$$$\mathrm{happy}\mathrm{new}\mathrm{year}!$$

Commented by Ar Brandon last updated on 01/Jan/23

Thank you, Sir �� Happy New Year ����

Answered by Ar Brandon last updated on 01/Jan/23

$$x^8+x^4+1={(x^4+1)}^2-x^4=(x^4-x^2+1)(x^4+x^2+1)$$$$I=\int \frac{dx}{x^8+x^4+1}=\int \frac{dx}{(x^4-x^2+1)(x^4+x^2+1)}$$$$=\frac{1}{2}\int \frac{(x^6+1)-(x^6-1)}{(x^4-x^2+1)(x^4+x^2+1)}dx$$$$=\frac{1}{2}\int \frac{x^2+1}{x^4+x^2+1}dx-\frac{1}{2}\int \frac{x^2-1}{x^4-x^2+1}dx$$$$=\frac{1}{2}\int \frac{1+\frac{1}{x^2}}{x^2+1+\frac{1}{x^2}}dx-\frac{1}{2}\int \frac{1-\frac{1}{x^2}}{x^2-1+\frac{1}{x^2}}dx$$$$=\frac{1}{2}\int \frac{1+\frac{1}{x^2}}{{(x-\frac{1}{x})}^2+3}dx-\frac{1}{2}\int \frac{1-\frac{1}{x^2}}{{(x+\frac{1}{x})}^2-3}dx$$$$=\frac{1}{2\sqrt{3}}\arctan \left(\frac{x^2-1}{\sqrt{3}x}\right)+\frac{1}{2\sqrt{3}}\mathrm{argcoth}\left(\frac{x^2+1}{\sqrt{3}x}\right)+C$$$$=\frac{1}{2\sqrt{3}}\arctan \left(\frac{x^2-1}{\sqrt{3}x}\right)+\frac{1}{4\sqrt{3}}\ln \mid \frac{x^2+\sqrt{3}x+1}{x^2-\sqrt{3}x+1}\mid +C$$$${\int }_0^{\mathrm{\infty }}\frac{dx}{x^8+x^4+1}={[\frac{1}{2\sqrt{3}}\arctan \left(\frac{x^2-1}{\sqrt{3}x}\right)+\frac{1}{4\sqrt{3}}\ln \mid \frac{x^2+\sqrt{3}x+1}{x^2-\sqrt{3}x+1}\mid ]}_0^{\mathrm{\infty }}$$$$\Rightarrow \overline{)\begin{array}{c}{\int }_0^{\mathrm{\infty }}\frac{dx}{x^8+x^4+1}=\frac{\pi }{2\sqrt{3}}\end{array}}$$

Answered by universe last updated on 01/Jan/23

Terms of Service

Privacy Policy

Contact: info@tinkutara.com