(((√x) + (√(x − 4a)))/( (√x) − (√(x − 4a)))) = a ≠ 0 find “x” in terms of “a”.


Question and Answers Forum

All Questions Topic List
Arithmetic Questions
Previous in All Question Next in All Question
Previous in Arithmetic Next in Arithmetic
Question Number 183989 by HeferH last updated on 01/Jan/23

$\frac{\sqrt{x} + \sqrt{x - 4 a}}{\sqrt{x} - \sqrt{x - 4 a}} = a \neq 0$ $f i n d ‘ ‘ x^{″} i n t e r m s o f ‘ ‘ a^{″} .$
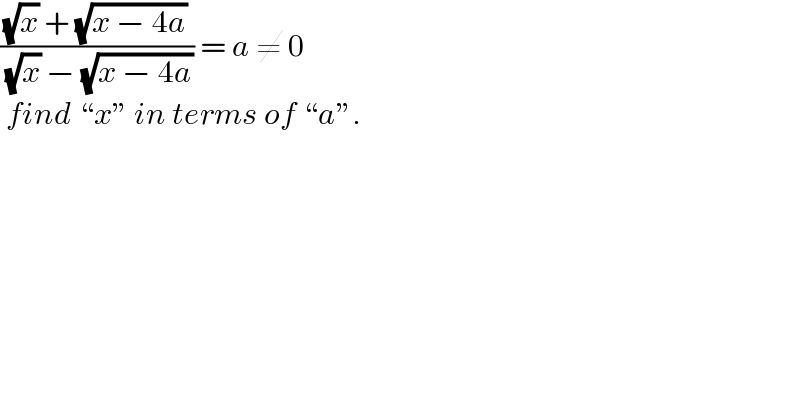
Commented by Frix last updated on 01/Jan/23

$I get x = {(a + 1)}^{2}$
	Answered by Rasheed.Sindhi last updated on 01/Jan/23

	$\frac{\sqrt{x} + \sqrt{x - 4 a}}{\sqrt{x} - \sqrt{x - 4 a}} = a \neq 0$ $f i n d ‘ ‘ x^{″} i n t e r m s o f ‘ ‘ a^{″} .$ $\frac{\sqrt{x} + \sqrt{x - 4 a}}{\sqrt{x} - \sqrt{x - 4 a}} + 1 = a + 1$ $\frac{2 \sqrt{x}}{\sqrt{x} - \sqrt{x - 4 a}} = a + 1$ $2 \sqrt{x} = a \sqrt{x} - a \sqrt{x - 4 a} + \sqrt{x} - \sqrt{x - 4 a}$ $a \sqrt{x} - \sqrt{x} = a \sqrt{x - 4 a} + \sqrt{x - 4 a}$ $\sqrt{x} (a - 1) = \sqrt{x - 4 a} (a + 1)$ $\frac{\sqrt{x - 4 a}}{\sqrt{x}} = \frac{a - 1}{a + 1}$ $\frac{x - 4 a}{x} = {(\frac{a - 1}{a + 1})}^{2}$ $1 - \frac{4 a}{x} = \frac{a^{2} - 2 a + 1}{a^{2} + 2 a + 1}$ $- \frac{4 a}{x} = \frac{a^{2} - 2 a + 1}{a^{2} + 2 a + 1} - 1 = \frac{- 4 a}{{(a + 1)}^{2}}$ $\frac{1}{x} = \frac{1}{{(a + 1)}^{2}} [∵ a \neq 0]$ $x = {(a + 1)}^{2}$
	Answered by a.lgnaoui last updated on 01/Jan/23

	$\frac{{(\sqrt{x} + \sqrt{x - 4 a})}^{2}}{4 a} = a$ $2 x - 4 a + 2 \sqrt{x (x - 4 a)} = 4 a^{2}$ $\sqrt{x (x - 4 a)} = 2 a^{2} + 2 a - x$ $x (x - 4 a) = 4 a^{4} + 4 a^{2} + x^{2} + 8 a^{3} - 4 a^{2} x - 4 a x$ $x^{2} - 4 a x = x^{2} - 4 a x (a + 1) + 4 a^{2} (a^{2} + 2 a + 1)$ $0 = 4 a^{2} {(a + 1)}^{2} - 4 a^{2} x$ $x = {(a + 1)}^{2}$
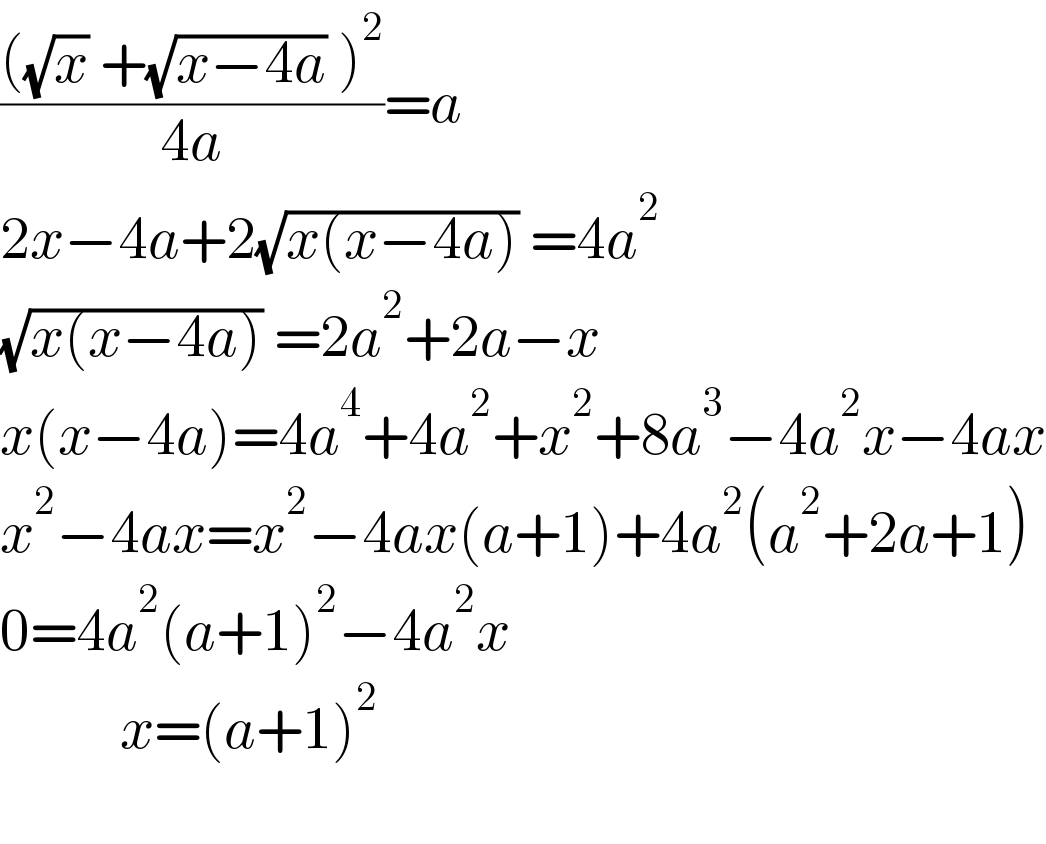
	Answered by manolex last updated on 01/Jan/23

	$m = \sqrt{x}$ $n = \sqrt{x - 4 a}$ $\frac{m + n}{m - n} = a$ $m^{2} = x$ $n^{2} = x - 4 a$ $m^{2} - n^{2} = 4 a$ $(m + n) (m - n) = 4 a$ $\frac{m + n}{m - n} = a m \neq n$ ${(m + n)}^{2} = 4 a^{2}$ $m + n = 2 a \lor m + n = - 2 a$ $m - n = 2 m - n = - 2$ $2 m = 2 a + 2 2 m = - 2 (a + 1)$ $m = a + 1 m = - (a + 1)$ $\sqrt{x} = a + 1 \sqrt{x} = - (a + 1)$ $x = {(a + 1)}^{2} x = {(a + 1)}^{2}$ $s o l u c i o n x = {(a + 1)}^{2}$ $c o m p r o b a c i o n$ $\frac{a + 1 + \sqrt{{(a + 1)}^{2} - 4 a}}{a + 1 - \sqrt{{(a + 1)}^{2} - 4 a}} = \frac{a + 1 + (a - 1)}{a + 1 - (a - 1)} = \frac{2 a}{2} = a c o r r e c t o$
	Answered by Rasheed.Sindhi last updated on 01/Jan/23

	$\frac{\sqrt{x} + \sqrt{x - 4 a}}{\sqrt{x} - \sqrt{x - 4 a}} = a \neq 0$ $f i n d ‘ ‘ x^{″} i n t e r m s o f ‘ ‘ a^{″} .$ $\sqrt{x} + \sqrt{x - 4 a} = a \sqrt{x} - a \sqrt{x - 4 a}$ $a \sqrt{x} - \sqrt{x} = \sqrt{x - 4 a} + a \sqrt{x - 4 a}$ $\sqrt{x} (a - 1) = \sqrt{x - 4 a} (a + 1)$ $\frac{\sqrt{x - 4 a}}{\sqrt{x}} = \frac{a - 1}{a + 1}$ $\frac{x - 4 a}{x} = \frac{a^{2} - 2 a + 1}{a^{2} + 2 a + 1}$ $\frac{x - 4 a}{x} - 1 = \frac{a^{2} - 2 a + 1}{a^{2} + 2 a + 1} - 1$ $\frac{- 4 a}{x} = \frac{- 4 a}{{(a + 1)}^{2}}$ $\frac{1}{x} = \frac{1}{{(a + 1)}^{2}} [∵ a \neq 0]$ $x = {(a + 1)}^{2}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum