Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 184040 by pete last updated on 02/Jan/23

Use implicit differentiation to find (d^2 y/dx^2 ) for siny = x

$$\mathrm{Use}\:\mathrm{implicit}\:\mathrm{differentiation}\:\mathrm{to}\:\mathrm{find}\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} } \\ $$$$\mathrm{for}\:\mathrm{sin}{y}\:=\:{x} \\ $$

Answered by cortano2 last updated on 02/Jan/23

y′cos y=1 y′′(−sin y)=0 y′′=0

$${y}'\mathrm{cos}\:{y}=\mathrm{1} \\ $$$${y}''\left(−\mathrm{sin}\:{y}\right)=\mathrm{0} \\ $$$${y}''=\mathrm{0} \\ $$

Answered by Yhusuph last updated on 02/Jan/23

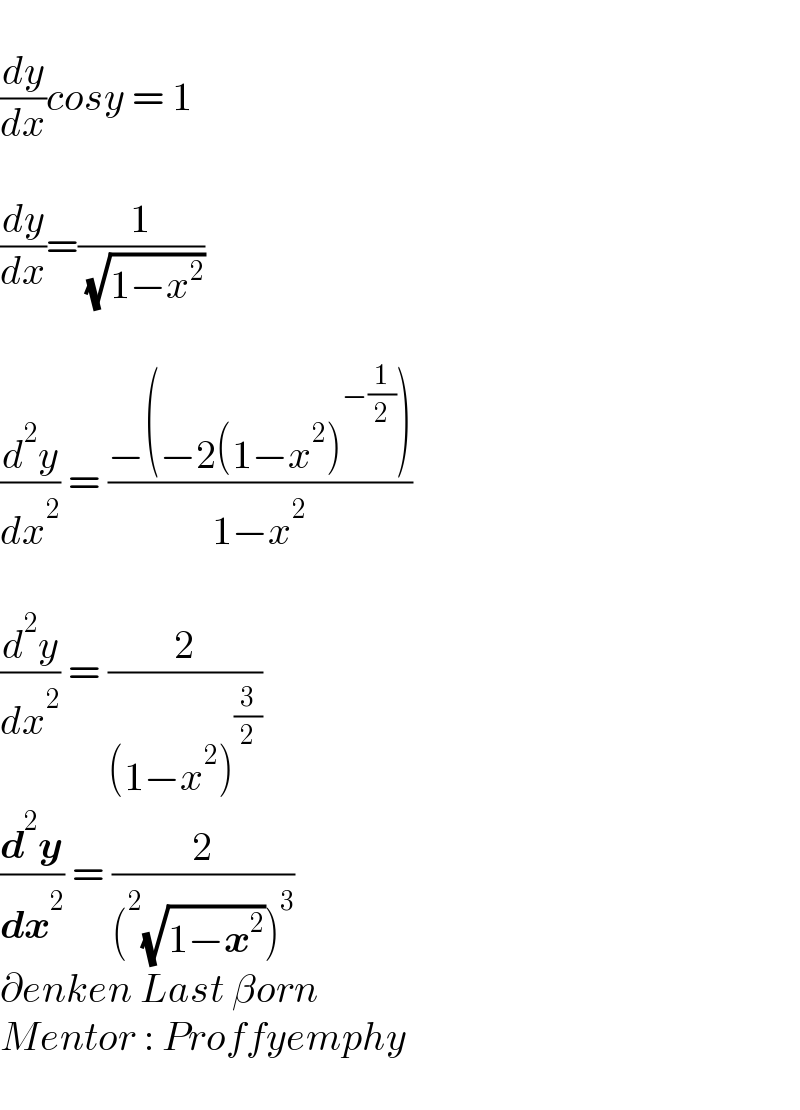
(dy/dx)cosy = 1 (dy/dx)=(1/( (√(1−x^2 )))) (d^2 y/dx^2 ) = ((−(−2(1−x^2 )^(−(1/2)) ))/(1−x^2 )) (d^2 y/dx^2 ) = (2/((1−x^2 )^(3/2) )) (d^2 y/dx^2 ) = (2/((^2 (√(1−x^2 )))^3 )) ∂enken Last βorn Mentor : Proffyemphy

$$ \\ $$$$\frac{{dy}}{{dx}}{cosy}\:=\:\mathrm{1} \\ $$$$ \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$ \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:=\:\frac{−\left(−\mathrm{2}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right)}{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$ \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:=\:\frac{\mathrm{2}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$\frac{\boldsymbol{{d}}^{\mathrm{2}} \boldsymbol{{y}}}{\boldsymbol{{dx}}^{\mathrm{2}} }\:=\:\frac{\mathrm{2}}{\left(^{\mathrm{2}} \sqrt{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }\right)^{\mathrm{3}} } \\ $$$$\partial{enken}\:{Last}\:\beta{orn} \\ $$$${Mentor}\::\:{Proffyemphy} \\ $$$$ \\ $$

Commented by Frix last updated on 02/Jan/23

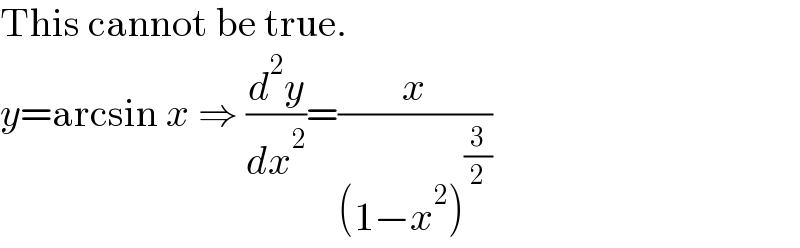
This cannot be true. y=arcsin x ⇒ (d^2 y/dx^2 )=(x/((1−x^2 )^(3/2) ))

$$\mathrm{This}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{true}. \\ $$$${y}=\mathrm{arcsin}\:{x}\:\Rightarrow\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$

Answered by mr W last updated on 03/Jan/23

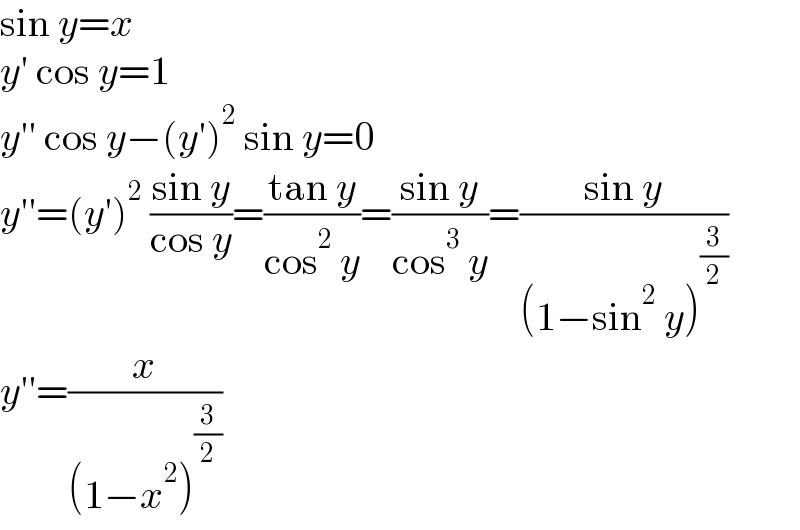
sin y=x y′ cos y=1 y′′ cos y−(y′)^2 sin y=0 y′′=(y′)^2 ((sin y)/(cos y))=((tan y)/(cos^2 y))=((sin y)/(cos^3 y))=((sin y)/((1−sin^2 y)^(3/2) )) y′′=(x/((1−x^2 )^(3/2) ))

$$\mathrm{sin}\:{y}={x} \\ $$$${y}'\:\mathrm{cos}\:{y}=\mathrm{1} \\ $$$${y}''\:\mathrm{cos}\:{y}−\left({y}'\right)^{\mathrm{2}} \:\mathrm{sin}\:{y}=\mathrm{0} \\ $$$${y}''=\left({y}'\right)^{\mathrm{2}} \:\frac{\mathrm{sin}\:{y}}{\mathrm{cos}\:{y}}=\frac{\mathrm{tan}\:{y}}{\mathrm{cos}^{\mathrm{2}} \:{y}}=\frac{\mathrm{sin}\:{y}}{\mathrm{cos}^{\mathrm{3}} \:{y}}=\frac{\mathrm{sin}\:{y}}{\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{y}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$${y}''=\frac{{x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$

Commented by pete last updated on 02/Jan/23

Thank you Mr. W, but the answer given is: (d^2 y/dx^2 ) = sec^2 ytany

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Mr}.\:\mathrm{W},\:\mathrm{but}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{given} \\ $$$$\mathrm{is}:\:\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:=\:\mathrm{sec}^{\mathrm{2}} \mathrm{ytany} \\ $$

Commented by cortano1 last updated on 03/Jan/23

from sin y = x we get { ((sec y=(1/( (√(1−x^2 )))))),((tan y=(x/( (√(1−x^2 )))))) :} now y′′= (x/((1−x^2 )(√(1−x^2 )))) = [(1/( (√(1−x^2 )))) ]^2 .(x/( (√(1−x^2 )))) = sec^2 y tan y

$$\:{from}\:\mathrm{sin}\:{y}\:=\:{x}\:{we}\:{get}\:\begin{cases}{\mathrm{sec}\:{y}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}}\\{\mathrm{tan}\:{y}=\frac{{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}}\end{cases} \\ $$$${now}\:{y}''=\:\frac{{x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\: \\ $$$$\:\:\:\:=\:\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\right]^{\mathrm{2}} .\frac{{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:=\:\mathrm{sec}\:^{\mathrm{2}} {y}\:\mathrm{tan}\:{y}\: \\ $$

Commented by mr W last updated on 03/Jan/23

you can express y′′ in terms of y or in terms of x. you see both above. y′′=(y′)^2 ((sin y)/(cos y))=((tan y)/(cos^2 y))=((sin y)/(cos^3 y))=((sin y)/((1−sin^2 y)^(3/2) )) y′′=(x/((1−x^2 )^(3/2) ))

$${you}\:{can}\:{express}\:{y}''\:{in}\:{terms}\:{of}\:{y}\:{or} \\ $$$${in}\:{terms}\:{of}\:{x}.\:{you}\:{see}\:{both}\:{above}. \\ $$$${y}''=\left({y}'\right)^{\mathrm{2}} \:\frac{\mathrm{sin}\:{y}}{\mathrm{cos}\:{y}}=\frac{\mathrm{tan}\:{y}}{\mathrm{cos}^{\mathrm{2}} \:{y}}=\frac{\mathrm{sin}\:{y}}{\mathrm{cos}^{\mathrm{3}} \:{y}}=\frac{\mathrm{sin}\:{y}}{\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{y}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$${y}''=\frac{{x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$

Commented by pete last updated on 04/Jan/23

Thanks very much sir

$$\mathrm{Thanks}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir} \\ $$

Answered by manxsol last updated on 02/Jan/23

$$ \\ $$$$ \\ $$

Commented by mr W last updated on 03/Jan/23

maybe not all people can read your solution properly. this is how your post looks like:

$${maybe}\:{not}\:{all}\:{people}\:{can}\:{read}\:{your} \\ $$$${solution}\:{properly}.\:{this}\:{is}\:{how}\:{your} \\ $$$${post}\:{looks}\:{like}: \\ $$

Commented by mr W last updated on 03/Jan/23

Commented by ARUNG_Brandon_MBU last updated on 03/Jan/23

Terms of Service

Privacy Policy

Contact: info@tinkutara.com