Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 184098 by paul2222 last updated on 02/Jan/23

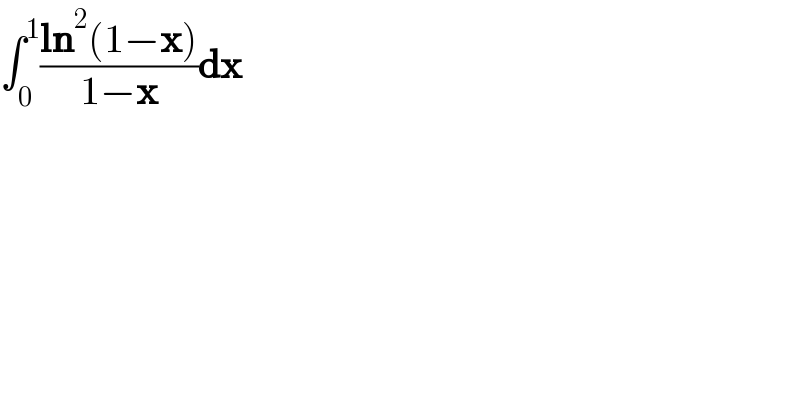
∫_0 ^1 ((ln^2 (1−x))/(1−x))dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{\mathrm{ln}}^{\mathrm{2}} \left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)}{\mathrm{1}−\boldsymbol{\mathrm{x}}}\boldsymbol{\mathrm{dx}} \\ $$

Commented by paul2222 last updated on 02/Jan/23

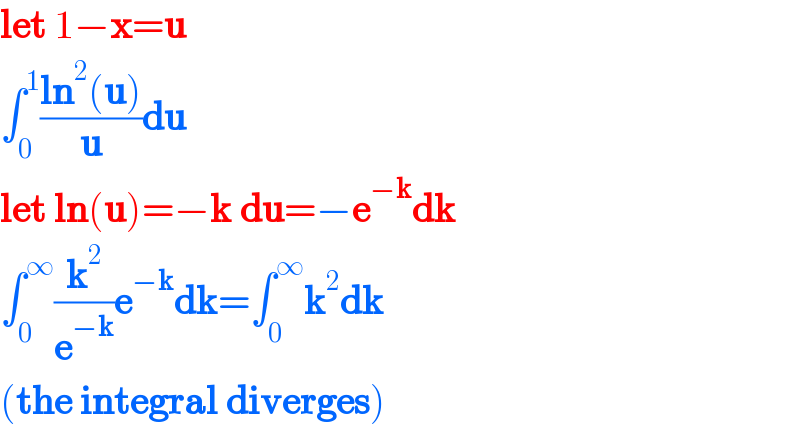
let 1−x=u ∫_0 ^1 ((ln^2 (u))/u)du let ln(u)=−k du=−e^(−k) dk ∫_0 ^∞ (k^2 /e^(−k) )e^(−k) dk=∫_0 ^∞ k^2 dk (the integral diverges)

$$\boldsymbol{\mathrm{let}}\:\mathrm{1}−\boldsymbol{\mathrm{x}}=\boldsymbol{\mathrm{u}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{\mathrm{ln}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{u}}\right)}{\boldsymbol{\mathrm{u}}}\boldsymbol{\mathrm{du}} \\ $$$$\boldsymbol{\mathrm{let}}\:\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{u}}\right)=−\boldsymbol{\mathrm{k}}\:\boldsymbol{\mathrm{du}}=−\boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{k}}} \boldsymbol{\mathrm{dk}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{\mathrm{k}}^{\mathrm{2}} }{\boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{k}}} }\boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{k}}} \boldsymbol{\mathrm{dk}}=\int_{\mathrm{0}} ^{\infty} \boldsymbol{\mathrm{k}}^{\mathrm{2}} \boldsymbol{\mathrm{dk}} \\ $$$$\left(\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{integral}}\:\boldsymbol{\mathrm{diverges}}\right) \\ $$

Commented by mokys last updated on 03/Jan/23

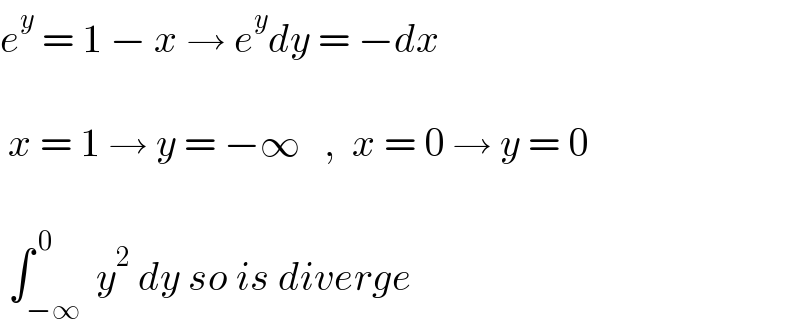
e^y = 1 − x → e^y dy = −dx x = 1 → y = −∞ , x = 0 → y = 0 ∫_(−∞) ^( 0) y^2 dy so is diverge

$${e}^{{y}} \:=\:\mathrm{1}\:−\:{x}\:\rightarrow\:{e}^{{y}} {dy}\:=\:−{dx} \\ $$$$ \\ $$$$\:{x}\:=\:\mathrm{1}\:\rightarrow\:{y}\:=\:−\infty\:\:\:,\:\:{x}\:=\:\mathrm{0}\:\rightarrow\:{y}\:=\:\mathrm{0} \\ $$$$ \\ $$$$\:\int_{−\infty} ^{\:\mathrm{0}} \:{y}^{\mathrm{2}} \:{dy}\:{so}\:{is}\:{diverge}\: \\ $$

Answered by Ml last updated on 03/Jan/23

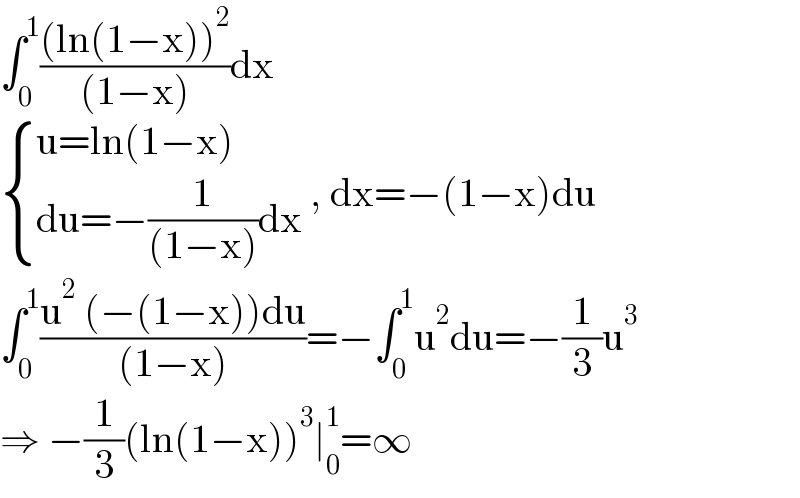
∫_0 ^1 (((ln(1−x))^2 )/((1−x)))dx { ((u=ln(1−x))),((du=−(1/((1−x)))dx)) :} , dx=−(1−x)du ∫_0 ^1 ((u^2 (−(1−x))du)/((1−x)))=−∫_0 ^1 u^2 du=−(1/3)u^3 ⇒ −(1/3)(ln(1−x))^3 ∣_0 ^1 =∞

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\right)^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{x}\right)}\mathrm{dx} \\ $$$$\begin{cases}{\mathrm{u}=\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}\\{\mathrm{du}=−\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{x}\right)}\mathrm{dx}}\end{cases}\:,\:\mathrm{dx}=−\left(\mathrm{1}−\mathrm{x}\right)\mathrm{du} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{u}^{\mathrm{2}} \:\left(−\left(\mathrm{1}−\mathrm{x}\right)\right)\mathrm{du}}{\left(\mathrm{1}−\mathrm{x}\right)}=−\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{u}^{\mathrm{2}} \mathrm{du}=−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{u}^{\mathrm{3}} \\ $$$$\Rightarrow\:−\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\right)^{\mathrm{3}} \mid_{\mathrm{0}} ^{\mathrm{1}} =\infty \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com